数组的优点:根据下标值访问效率会很高。
数组的缺点。在插入和删除数据时,需要进行大量的位移操作,效率很低;根据元素来查找,需要进行线性查找,效率就会比较低,比较好的方式是先对数组进行排序,生成有序数组,再进行二分查找,才能提高查找效率。
链表的优点:插入和删除操作效率都很高。
链表的缺点:查找效率很低,需要从头部或者尾部开始依次访问链表中的每个数据项,直到找到;即使插入和删除操作效率很高,但是如果要插入和删除中间位置的元素的话,还是需要从头或尾先找到对应的数据。
哈希表的优点:插入、查询和删除效率都很高。
哈希表的缺点:空间利用率不高,底层使用的数组,并且某些单元是没有被利用的;哈希表中的元素是无序的,不能按照固定的顺序来遍历哈希表中的元素;不能快速地找出哈希表中的最大值或者最小值这些特殊的值。
树是由 n 个节点组成的一个具有层次关系的集合。把它叫做树是因为它看起来像一颗倒挂的树,它是根朝上,而叶朝下的。树结构是非线性的,可以表示一对多的关系。
生活中的树的案例:
公司的组织架构: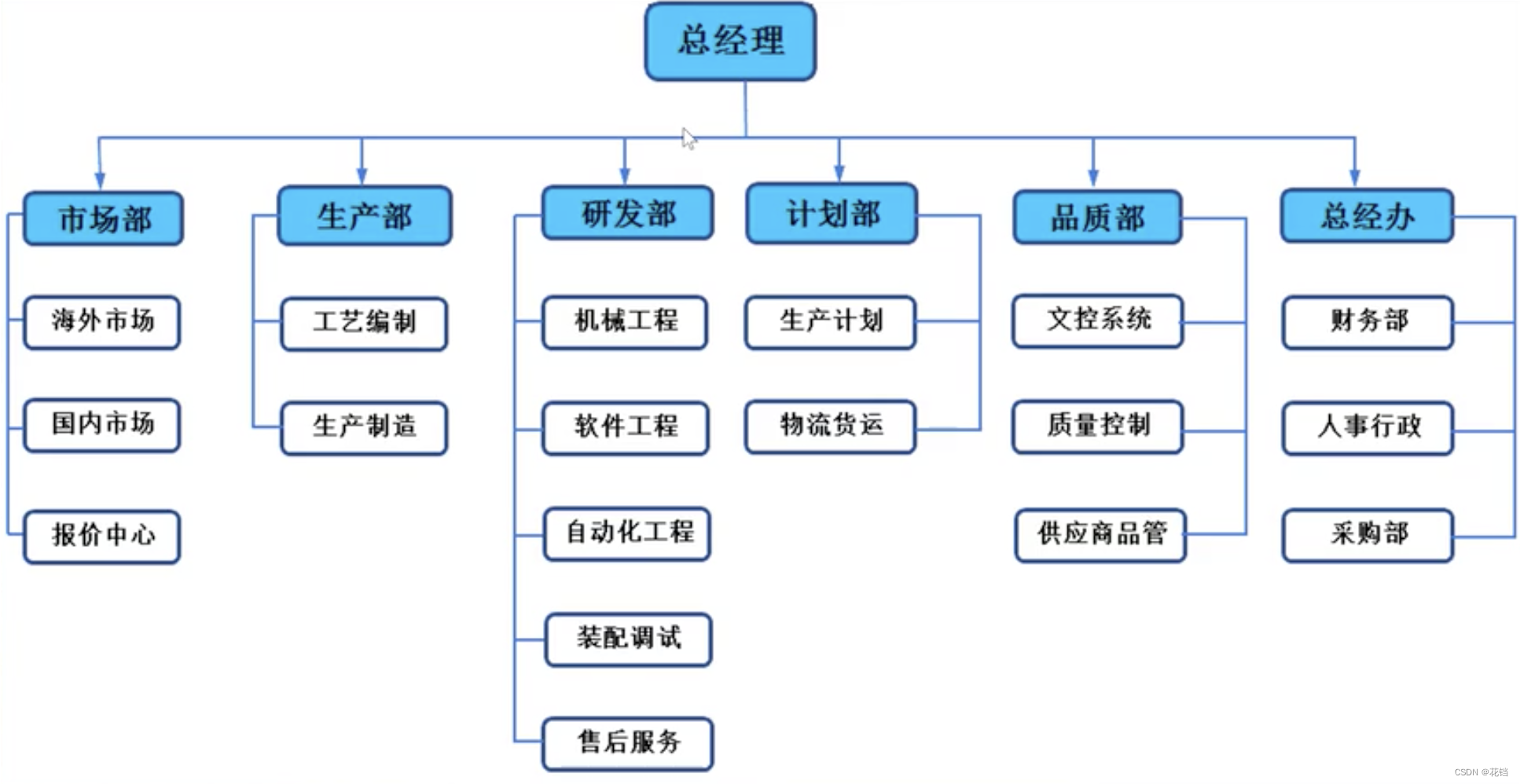
家谱:
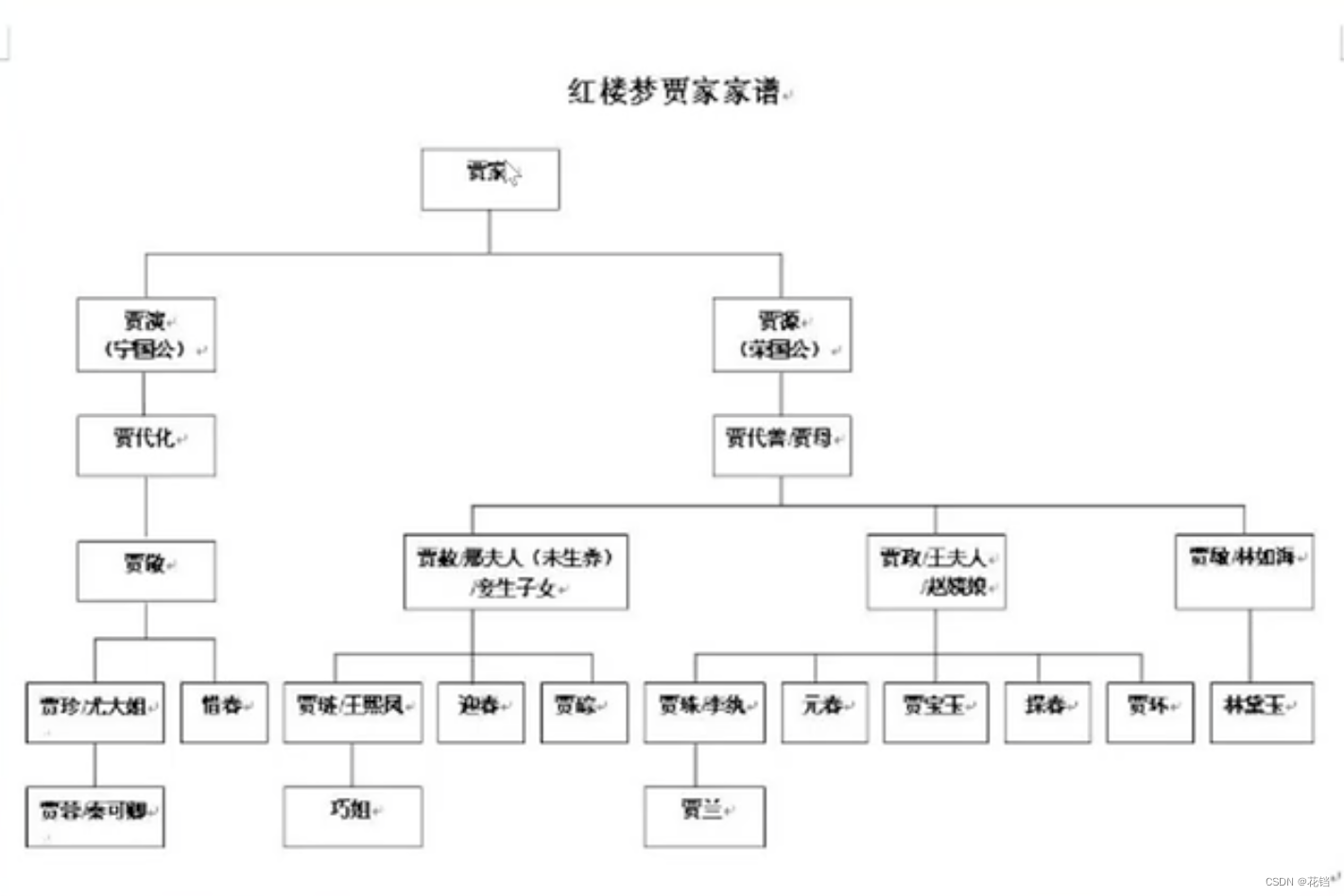
树的术语:
- 树:是由 n 个节点组成的一个具有层次关系的结合。当 n = 0 时,称为空树;当 n > 0 时,称为非空树。
子树:对于任意一颗非空树,除了根节点外的其余节点可分为 m 个互不相交的有限集 T1、T2…Tm,其中每个集合本身又是一棵树,称为原来树的子树。
森林:m 棵互不相交的树的集合称为森林。 - 树的度:树的所有节点中最大的度数。
节点的度:一个节点含有的子树的个数。 - 树的深度:树中所有节点中的最大层次。
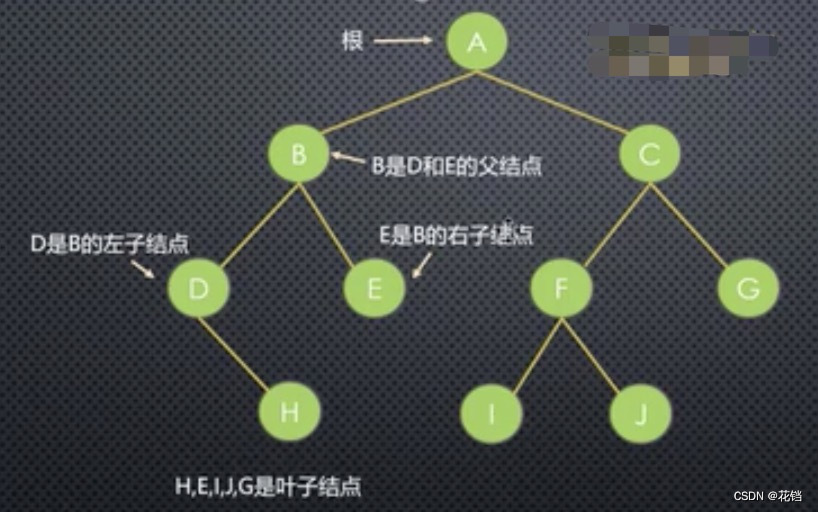
节点的层次:根节点的层次为 1,根的子节点的层次为 2,以此类推。 - 路径:从节点 A 到节点 H 的路径为一个节点序列 A、B、D、H。
路径长度:路径所包含的边的个数,从节点 A 到节点 H 的路径长度为 3。
边:节点 A 到节点 B 之间的这条线就称为边。 - 根节点:没有父节点的节点称为根节点。
叶子节点:度为 0 的节点。
父节点:若一个节点含有子节点,则这个节点就是其子节点的父节点。
子节点:一个节点含有的子树的根节点称为该节点的子节点。
祖先节点:从根节点到该节点所经分支上的所有节点。
子孙节点:以某节点为根的子树中的任一节点都是该节点的子孙节点。
兄弟节点:具有同一父节点的各节点彼此是兄弟节点。
堂兄弟节点:父节点在同一层次的节点互为堂兄弟节点。
树的表示方法:
- 普通的表示方法:每个节点中包含节点自身和它的子节点。由于子节点的个数不确定,导致这种存储方式内部的属性不确定。不推荐。
Node D: this.data = data this.leftChild = H this.rightChild = J this.middleChild = I ... // 如果还有其他子节点,需要接着存储进来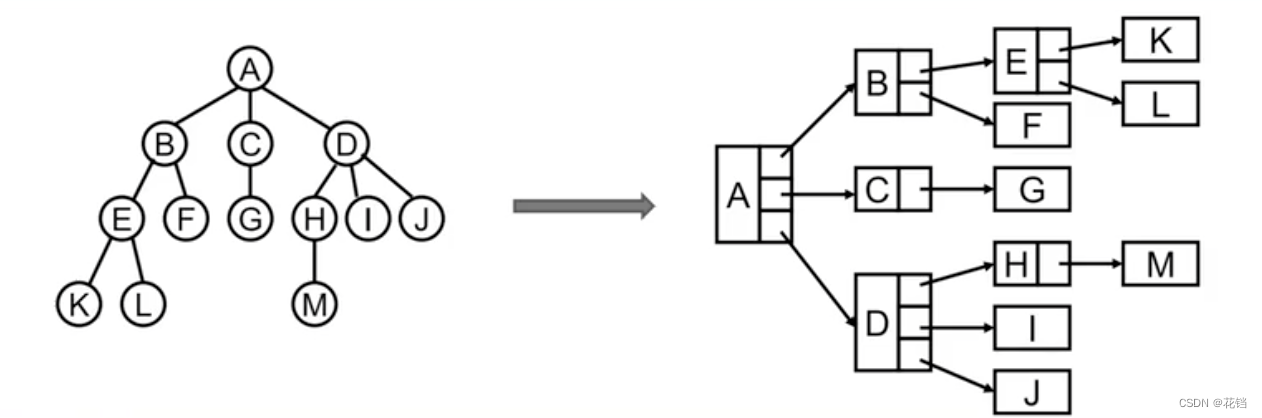
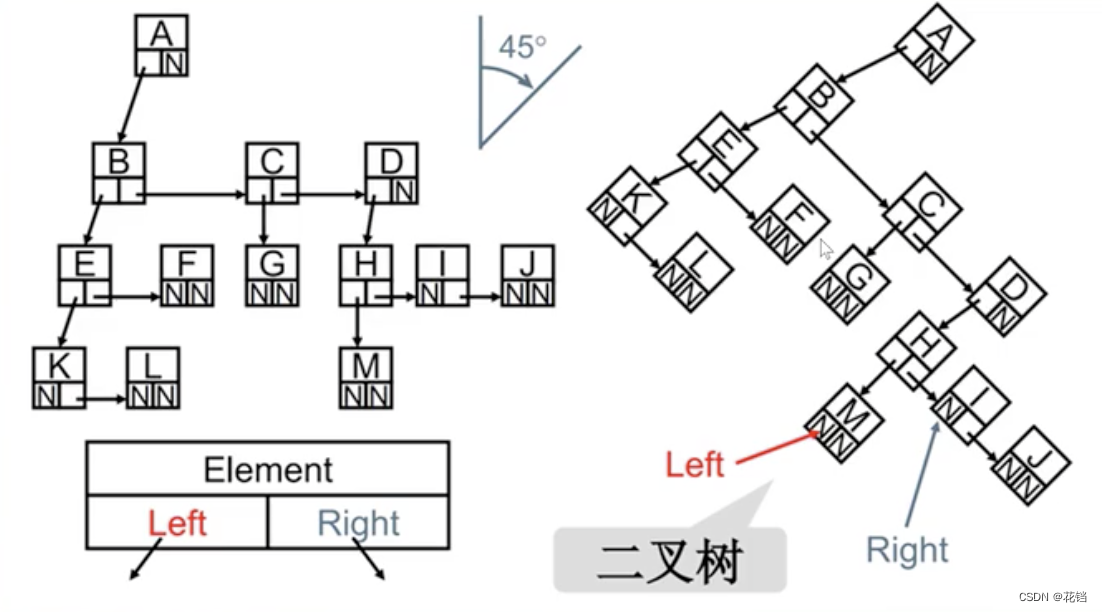
- 儿子-兄弟表示法:每个节点中包含节点自身、它的左子节点和它的右兄弟节点。推荐。
Node C: this.data = data this.leftChild = G this.rightSibling = D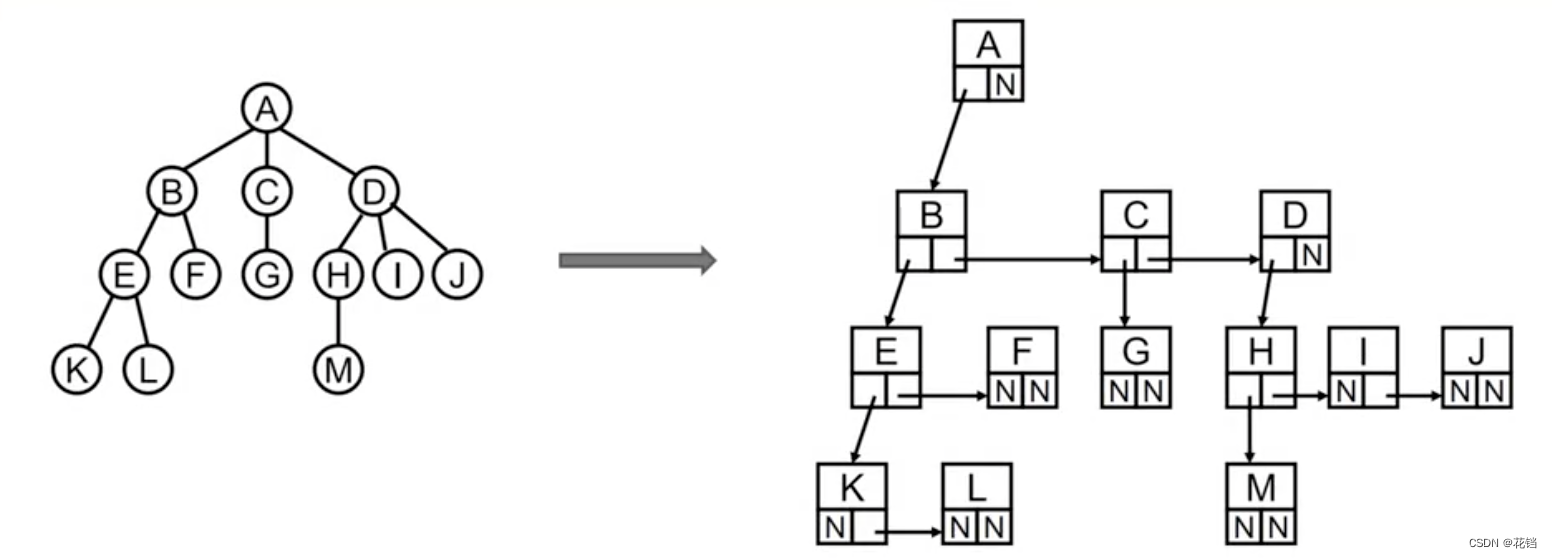
二叉树:
二叉树:如果树中的每个节点最多只有两个子节点,这样的树就称为二叉树。
所有的树本质上都可以使用二叉树模拟出来。
上面的例子并不是二叉树,将它用儿子-兄弟表示法表示,并旋转 45 度,就可以看到模拟成了一颗二叉树。
二叉树的特性:
- 一个二叉树的第 i 层的最多有
2^(i - 1),i >= 1个节点。第 1层最多有 1 个节点,第 2 层最多有 2 个节点,第 3 层最多有 4 个节点… - 一个深度为 k 的二叉树最多有
2 ^ k - 1,k >= 1个节点。第 1层最多有 1 个节点,第 2 层最多有 3 个节点,第 3 层最多有 7 个节点… - 对于任何非空二叉树,如果用 n0 来表示叶子节点的个数,用 n2 来表示度为 2 的节点的个数,那么 n0 = n2 + 1。
二叉树的表示方式:
二叉树最常见的存储方式是使用链表。
每个节点封装成一个 Node,Node 中包含节点本身的数据、左节点的引用和右节点的引用。
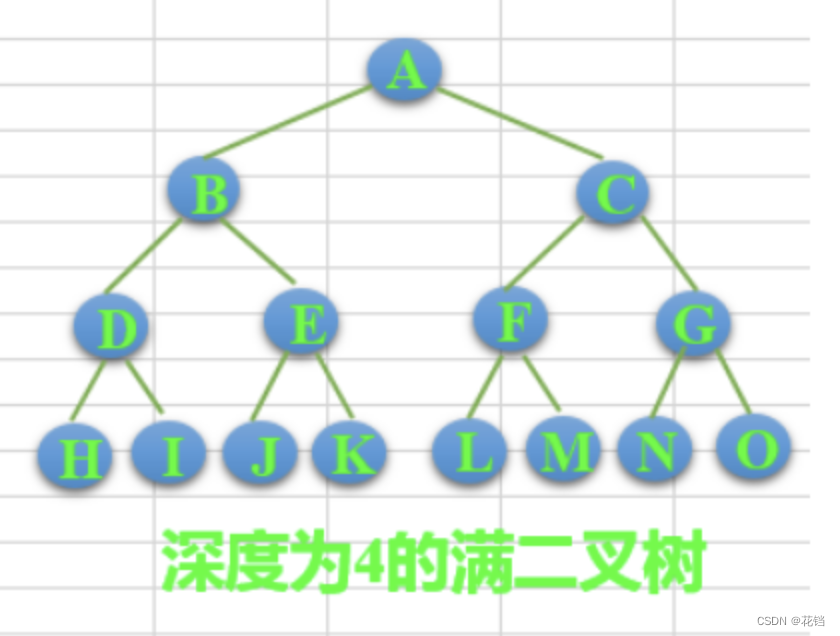
完美二叉树(满二叉树):
完美二叉树(满二叉树):对于一棵二叉树,假设其深度为 d,除了第 d 层外,其余各层的节点都有左右两个子节点,且叶子节点都处在第 d 层。
完全二叉树:
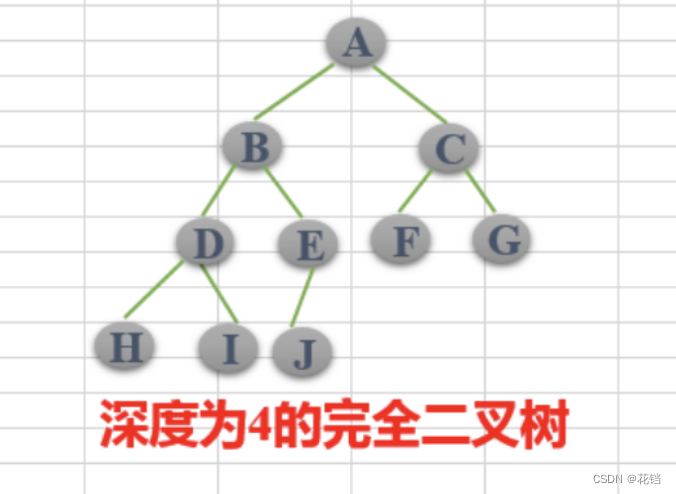
完全二叉树:对于一棵二叉树,假设其深度为 d,除了第 d 层外,其余各层的节点数都已达到最大值,且第 d 层的叶子节点从左到右连续存在(也就是说,即使缺少节点,也只能缺少右侧的节点,从左到右必须是连续的)。
完美二叉树是特殊的完全二叉树。
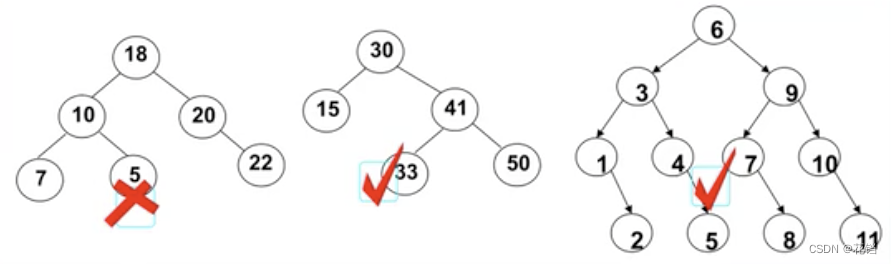
二叉搜索树(BST、Binary Search Tree、二叉排序树、二叉查找树):
二叉搜索树:不管是哪个节点,它的左子树的节点的值都小于它,右子树的节点的值都大于它。
二叉搜索树的特点就是相对较小的值总是保存在左节点上,相对较大的值总是保存在右节点上,这一特性使得查找的效率非常高。