基于哈希的DOM Diff算法

DOM基本操作

DOM基本操作类型

对DOM的基本操作可概括如下：

操作原语	描述
child i	将游标设为当前的第 $i$ 个子节点
parent	将游标设为当前的父节点
remove i	移除第 $i$ 个子节点
append html	增加一个子节点，内容为html
modify attr x / reset attr	修改或重置attr属性
sort indices	按照indices对子节点顺序重排

其中child和parent对应了树上移动，remove、append和sort能对树形结构进行更改，modify和reset对节点进行修改。显然用这些基本操作来描述如何将一个DOM树变换为另外一个DOM树是完备的。

事实上，去除sort，其他操作也是完备的，因为sort等价于remove和append的结合。但是由于代价因素，有必要引入此操作。

DOM基本操作代价

之所以需要Diff算法，就是要寻找一个低的代价将一个DOM树转化成另一个DOM树。如果抛开代价，那么Diff算法就失去了实际意义。（不计代价则可直接使用整体替换的方式）

所以说引入基本操作的概念，也是为了将整个过程细粒度化，从而优化掉部分非必要的操作。当然，基本操作在执行代价上并非等价的，通过经验估计可以得到它们的开销级别：

操作	代价	解释
`append`	大	解析HTML，生成完整的节点或子树
`remove`	小	指针变化，触发GC时较大
`sort`	小	多指针变化，需要遍历一遍孩子
`modify`	小	赋值；少数情况下需要解析
`child`	极小	指针变化
`parent`	极小	指针变化

通过对代价的分析，我们可以得出结论：Diff中的结果应当尽可能少的使用append，其他操作可以近似同等考虑，并且指针操作可以忽略代价。

Diff算法

基于同层次的遍历

常见的Diff算法都是基于同层次的，例如其他框架中的DOM Diff、Git中的文件树Diff。这么做的好处就是不需要考虑纵向的复用，只需要考虑同层次的复用，从而使得算法更简单。

其步骤就是使用双指针，指针进行相同的移动，分别指向两棵树的同层级部分。于是我们可以边遍历，边处理差异。

指针的移动原则

指针的移动并非对孩子依次进行，而是按照一定原则进行。具体而言，就是按照算法认为差异的但修改的代价最小的进行。算法按照这样的原则选中的两个节点形成一个配对，从而递归进行一个子树到另一个子树的变换过程。

子树的Diff

差异分为三个级别：子树、儿子、属性。最有利的情况就是子树相同。对于判断子树相同，我们可以使用之前的哈希树，以常数时间判断。显然，对于子树相同，我们可以直接跳过。否则我们需递归进行。

属性的Diff

对于算法中双指针移动到的两个节点，我们认为它们是差异的。首先一个必要的步骤是比较节点上的属性差异。基于哈希，我们首先检查属性的哈希，如果属性相同，显然可以跳过；否则遍历属性找不同。

子元素的Diff

子元素的Diff是一个复杂的复合问题，我们将它分解成三个子问题：
(1). 寻找两个子元素，递归进行Diff
(2). 找到哪些子元素被添加了
(3). 找到哪些子元素被删除了

子问题(1)

子问题(1)是算法的核心问题，属于是决策问题，它需要体现指针移动原则中的最小代价。基于贪心的思路，可以设计如下的配对过程：
1. 找到子树完全相同的两个节点
2. 对于子树不完全相同的两个节点：
  1. 找到标签相等，且内部元素相等的两个节点
  2. 找到标签相等，且属性相等的两个节点
  3. 找到标签相等的两个节点
对于1，也就是子树Diff过程，这两个节点可以直接被跳过，代价最低；对于2.1，仅该层节点出现差异，其子孙无差异，代价很低；对于2.2，该层节点无差异，但其子孙有差异，代价未知；对于2.3，均有差异，但类型相同，代价未知但一定高于2.2。

按照如上顺序执行配对，对于1和2.1显然是最优的，但2.2与2.3只能近似优化，原因是深于子节点层次的情况我们是不知道的，只能贪心地进行下去。
子问题(2)和(3)

在子问题(1)基础上，对于标签不等的，前一个子元素集合中剩下的未配对的就是被删除的元素；后一个子元素集合中剩下的未配对的就是被增加的元素。

算法伪代码

A - B：
- 比较tag
    1. tag不等 => 移除B，增加A
    2. tag相等 => dynamic_cast
- 比较属性
    1. A中属性与B中不等
        1. A中属性为默认值 => 重置属性
        2. A中属性不为默认值 => 设置属性 
- 比较inner_elements
    1. 对于outer_hash相等的配对（完全相同） => 排序
    2. 对于outer_hash不等的配对
        1. 寻找tag相等且inner_hash相等的配对（属性变更） => 递归
        2. 寻找tag相等且attribute_hash相等的配对（内部元素变更） => 递归
        3. 寻找tag相等的配对（内部元素变更且属性变更）=> 递归
        4. tag不等
            1. 在A中剩下的 => 增加
            2. 在B中剩下的 => 移除
    3. 按照配对排序

复杂度分析

对于子元素Diff算法，使用散列映射优化，能够将复杂度优化为 $O (m)$ ， $m$ 表示子元素个数。

对总体，最坏情况下是 $O (n)$ 。在每次只进行一个操作的假设下，对满叉树而言，平均复杂度为 $O (l o g n)$ 。

代价分析

最坏代价肯定是替换整棵树，这是基于两棵树完全不同的最坏假设而言的。在每次只进行一个操作的假设下，对满叉树而言，代价比较平均，除非出现子树的整体移动。

二看Diff算法

优点和缺点

优点

算法简单，执行效率高。
缺点

无法优化整体移动的代价：

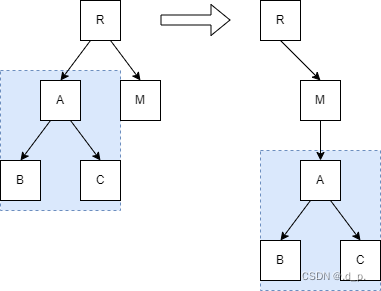
基于同层次的Diff算法无法识别这种移动情形，最终的结果仍然是先删后增。

对于本项目

本项目中SVG的DOM结构层级比较少，且整体移动的情况很罕见，故坏情况的出现概率非常低。相反，组件在本项目中被设计的的组织结构恰好为同层次结构，因此上述算法对本项目的针对性相当强。

核心代码

子元素Diff

void SVGElement::inner_differ(const SVGElement &element,
        std::vector<_el_idx> &removal,
        std::vector<_el_idx> &addition,
        std::vector<std::pair<_el_idx, _el_idx>> &unchanged,
        std::vector<std::pair<_el_idx, _el_idx>> &changed) const {
    std::function<const std::string(const std::shared_ptr<SVGElement> &)> get_tag;
    get_tag = [](const std::shared_ptr<SVGElement> &x){
        if (x->get_raw_HTML() != STR_NULL) return std::string("#") + std::to_string(x->get_outer_hash());
        return std::string(x->get_tag());
    };
    std::unordered_map<std::string, std::set<_el_idx>> tags_map;
    std::set<_el_idx> A, B;
    int c = 0;
    for (auto &a : _inner_elements) A.insert({a, c++}); c = 0;
    for (auto &b : element.get_inner_elements()) tags_map[get_tag(b)].insert({b, c}), B.insert({b, c++});

    c = 0;
    for (auto &_a : _inner_elements) { // with outer hash equal
        auto &tag  = get_tag(_a);
        _el_idx a = { _a, c++ };
        if (!A.count(a) || !tags_map.count(tag)) continue;
        _el_idx match = { nullptr, -1 };
        for (auto &b : tags_map[tag]) {
            if (b.ptr->get_outer_hash() == a.ptr->get_outer_hash()) {
                match = b;
                break;
            }
        }
        if (match.idx >= 0) {
            tags_map[tag].erase(match);
            A.erase(a), B.erase(match);
            unchanged.push_back({a, match});
        }
    }
    c = 0;
    for (auto &_a : _inner_elements) { // with inner hash equal
        auto &tag  = get_tag(_a);
        _el_idx a = { _a, c++ };
        if (!A.count(a) || !tags_map.count(tag)) continue;
        _el_idx match = { nullptr, -1 };
        for (auto &b : tags_map[tag]) {
            if (b.ptr->get_inner_hash() == a.ptr->get_inner_hash()) {
                match = b;
                break;
            }
        }
        if (match.idx >= 0) {
            tags_map[tag].erase(match);
            A.erase(a), B.erase(match);
            changed.push_back({a, match});
        }
    }
    c = 0;
    for (auto &_a : _inner_elements) { // with attribute hash equal
        auto &tag  = get_tag(_a);
        _el_idx a = { _a, c++ };
        if (!A.count(a) || !tags_map.count(tag)) continue;
        _el_idx match = { nullptr, -1 };
        for (auto &b : tags_map[tag]) {
            if (b.ptr->get_attribute_hash() == a.ptr->get_attribute_hash()) {
                match = b;
                break;
            }
        }
        if (match.idx >= 0) {
            tags_map[tag].erase(match);
            A.erase(a), B.erase(match);
            changed.push_back({a, match});
        }
    }
    c = 0;
    for (auto &_a : _inner_elements) { // with tag equal
        auto &tag  = get_tag(_a);
        _el_idx a = { _a, c++ };
        if (!A.count(a) || !tags_map.count(tag) || tags_map[tag].size() == 0) continue;
        _el_idx match = *tags_map[tag].begin();
        tags_map[tag].erase(match);
        A.erase(a), B.erase(match);
        changed.push_back({a, match});
    }
    for (auto &a : A) addition.push_back(a);
    for (auto &b : B) removal.push_back(b);
}

属性Diff

const std::string SVGElement::attribute_differ(const SVGElement &element) const {
    std::stringstream ss;

    if (_id != element.get_id()) {
        if (_id == STR_NULL) ss << "reset id" << std::endl;
        else ss << "modify id \"" << _id << "\"" << std::endl;
    }
    if (_lang != element.get_lang()) {
        if (_lang == STR_NULL) ss << "reset lang" << std::endl;
        else ss << "modify lang \"" << _lang << "\"" << std::endl;
    }
    // 省略其他数百个属性...
}

Diff = 子树Diff + 属性Diff + 子元素Diff

const std::string SVGElement::operator-(const SVGElement &element) const {
    std::stringstream ss;

    // tag differ
    if (get_tag() != element.get_tag()) {
        auto svg = outer_SVG();
        ss << "replace " << svg.size() << std::endl << svg << std::endl;
        return ss.str();
    }

    // cast
    auto _element = static_cast<const SVGElement &>(element);

    // attribute differ
    if (element.get_attribute_hash() != get_attribute_hash()) ss << attribute_differ(_element);

    // inner differ
    if (element.get_inner_hash() == get_inner_hash()) return ss.str();

    // extract change relation
    std::vector<_el_idx> removal;
    std::vector<_el_idx> addition;
    std::vector<std::pair<_el_idx, _el_idx>> unchanged;
    std::vector<std::pair<_el_idx, _el_idx>> changed;
    inner_differ(element, removal, addition, unchanged, changed);
    // remove
    int m = _inner_elements.size(), n = element.get_inner_elements().size();
    int *indices = new int[m], *removed = new int[n];
    std::fill(indices, indices + m, 0); std::fill(removed, removed + n, 0);
    for (auto &r : removal) removed[r.idx] = 1;
    for (int i = 1; i < n; i++) removed[i] += removed[i - 1];
    for (auto &r : removal) ss << "remove " << r.idx - (r.idx > 0 ? removed[r.idx - 1] : 0) << std::endl;
    // append
    for (auto &a : addition) {
        auto svg = a.ptr->outer_SVG();
        ss << "append " << svg.size() << std::endl << svg << std::endl;
    }
    // change recursively
    for (auto &c : changed) {
        auto &a = c.first; auto &b = c.second;
        ss << "child " << b.idx - removed[b.idx] << std::endl;
        ss << (*a.ptr - *b.ptr);
        ss << "parent" << std::endl;
    }
    // sort
    for (auto &c : unchanged) {
        auto &a = c.first; auto &b = c.second;
        indices[b.idx - removed[b.idx]] = a.idx;
    }
    for (auto &c : changed) {
        auto &a = c.first; auto &b = c.second;
        indices[b.idx - removed[b.idx]] =  a.idx;
    }
    for (int i = 0; i < addition.size(); i++) {
        auto &a = addition[i];
        indices[unchanged.size() + changed.size() + i] = a.idx;
    }
    bool ordered = true;
    for (int i = 0; i < m && ordered; i++) if (indices[i] != i) ordered = false;
    if (!ordered) {
        ss << "sort \"";
        for (int i = 0; i < m; i++) {
            ss << indices[i];
            if (i < m - 1) ss << ",";
        }
        ss << "\"" << std::endl;
    }
    delete[] removed; delete[] indices;

    return ss.str();
}