一、什么是回溯法?
- 💛 回溯法的定义:是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
- 💚 回溯法的应用:

- 💙 回溯法的模板:
public void backtracing(参数列表){
if(终止条件){
存放结果;
return;
}
for(选择 : 选择列表){
做选择;
backtracking(路径, 选择路径);
回溯,撤销选择;
}
}
- ?? 如何理解回溯法:
根据问题去创建一个用于搜索所有解N叉树,遍历其中的结点,如果满足条件就进行选择,然后将选择操作重置回溯到进行选择操作前的状态。
通过穷举来寻找问题的答案,可以通过剪枝法来提高回溯的效率,但是这种算法的效率还不是很高,但因为某些问题只能用这个算法来求解,所以这个算法没有被淘汰。
回溯法是通过递归来完成的,递归有结束条件,回溯法也要设置终止条件。
二、回溯法的具体应用
1.全排列问题
- 问题描述:
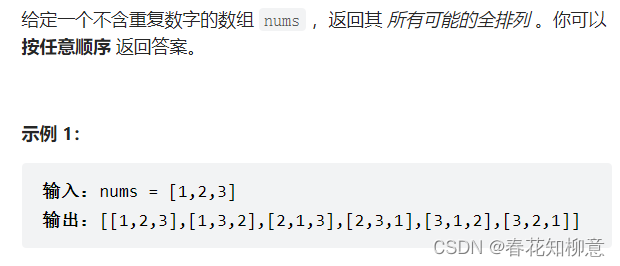
这里引用代码随想录的全排列分析图:
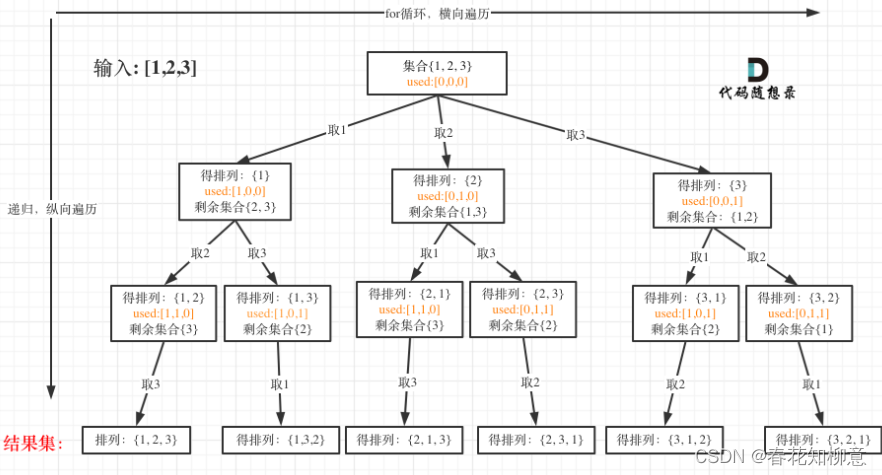
📝 解题思路:
(1)创建两个集合,一个用来保存排序的结果,一个保存排序结果的集合
(2)可以设置一个布尔型的数组,来表示当前元素是否已经出现在组合中了
(3)当保存排列结果组合的长度等于了数组的长度,说明此时该集合中的元素已经包含了数组中的全部元素,然后将其添加到结果集合中即可。
- Java版本:
class Solution {
//存放排列结果的集合
private List<List<Integer>> result = new ArrayList<List<Integer>>();
//存放排列结果
private LinkedList<Integer> path = new LinkedList<Integer>();
public void permuteBackTracking(int [] nums){
//当前集合已经构成一种排列的情况
if(path.size() == nums.length){
result.add(new ArrayList<Integer>(path));
return;
}
for(int i = 0; i < nums.length; i++){
//当前元素是否已经存在于path集合
if(path.contains(nums[i])){
continue;
}
//更新
path.add(nums[i]);
permuteBackTracking(nums);
//回溯
path.removeLast();
}
}
public List<List<Integer>> permute(int[] nums) {
//调用方法选择全排列
permuteBackTracking(nums);
//返回结果
return result;
}
}
2.N皇后问题
- 问题描述:
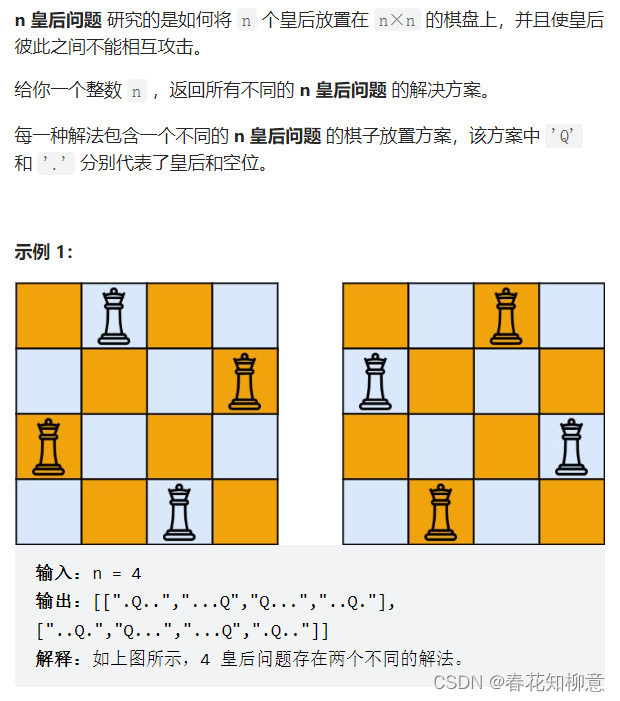
皇后问题:皇后们不能出现在同行,同列和对角线上
N皇后是回溯法的一个经典题,那么如何进行回溯呢?
类似于下棋,去放置好一个皇后时,其余皇后的位置将会受到限制
算法要求最后返回的是一个集合子集合为字符串类型,但是我们直接用字符串去模拟每一行的话,不利于修改皇后的位置和判断是否冲突,所以采用二维字符数组来模拟棋盘
这就导致为结果集合添加子集合时,需要将二维字符数组转化为字符串类型的集合:
//创建一个字符串集合
ArrayList<String> str = new ArrayList<String>();
//遍历二维字符串数组
for(char [] ch : chessbord){
str.add(String.copyValueOf(ch));
}
需要判断如果在当前位置放皇后,是否满足条件:行、列、对角线
//声明: row代表行 col代表列 n代表皇后的个数 chessword代表棋盘
//因为每放置一个皇后就会递归进入下一行,所以不会出现两个皇后在同一行的情况
//判断是否满足皇后们不在同一列
for(int i = 0; i < row; i++){
if(chessboard[i][col] == 'Q'){
return false;
}
}
// 检查45度对角线
for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查135度对角线
for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
接下来就为回溯法里面的内容了,判断当前行是否和皇后的个数相同,如果相同说明已经完成了一种N皇后的放置。
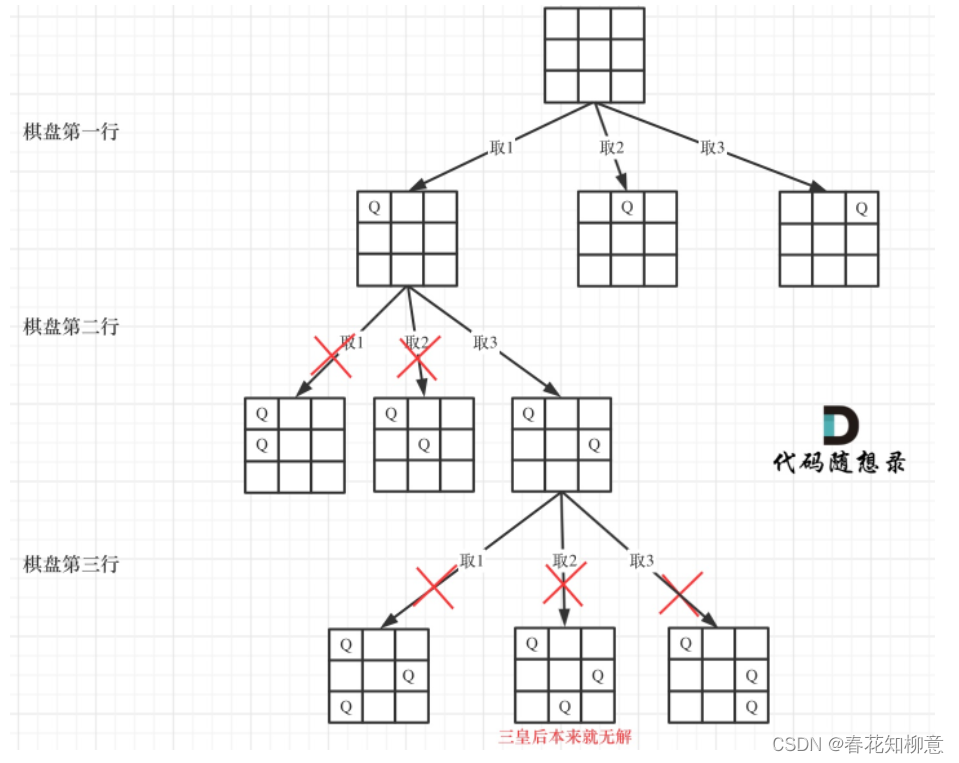
之后直接套用回溯法的模板即可。
- Java版本:
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] chessboard = new char[n][n];
for (char[] c : chessboard) {
Arrays.fill(c, '.');
}
backTrack(n, 0, chessboard);
return res;
}
public void backTrack(int n, int row, char[][] chessboard) {
if (row == n) {
res.add(Array2List(chessboard));
return;
}
for (int col = 0;col < n; ++col) {
if (isValid (row, col, n, chessboard)) {
chessboard[row][col] = 'Q';
backTrack(n, row+1, chessboard);
chessboard[row][col] = '.';
}
}
}
public List Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] c : chessboard) {
list.add(String.copyValueOf(c));
}
return list;
}
public boolean isValid(int row, int col, int n, char[][] chessboard) {
// 检查列
for (int i=0; i<row; ++i) { // 相当于剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查45度对角线
for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查135度对角线
for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
}
3.组合问题
- 问题描述:

与排列问题类似,区别在于排列是有序的,而组合是无序的。
根据回溯法的算法模板:
public void backtracing(参数列表){
if(终止条件){
存放结果;
return;
}
for(选择 : 选择列表){
做选择;
backtracking(路径, 选择路径);
回溯,撤销选择;
}
}
来思考解决组合问题的步骤,回溯法三部曲:
(1)确定回溯函数的参数
(2)回溯函数终止条件
(3)单层回溯过程
- 回溯函数的参数
根据算法题的要求,答案通过返回值来带回,要求用集合来完成。
我们创建两个集合,一个保存一种组合的结果,一个保存全部组合的结果。【为了方便直接定义为全局变量,增加可读性】
此时参数列表只需要传入元素个数n, 和组合中包含元素的个数k
- 回溯函数终止条件
当组合集合中元素个数与要求的个数相同时,说明已经满足条件,将该组合的集合添加到结果集合中即可
- 单层回溯过程
如果当前集合不为空,并且集合中不包含当前元素或当前元素不小于集合中的前一个元素,那么直接回到循环首部,进行下一次循环
Java版本详解:
class Solution {
//创建保存全部结果的集合
List<List<Integer>> res = new ArrayList<List<Integer>>();
//创建保存一个结果的集合
LinkedList<Integer> path = new LinkedList<Integer>();
public void combineBackTraking(int n, int k){
if(path.size() == k){
res.add(new ArrayList<Integer>(path));
return;
}
for(int i = 1; i <= n; i++){
if(path.size() != 0 && (path.contains(i) || i < path.getLast())){
continue;
}
path.add(i);
combineBackTraking(n, k);
path.removeLast();
}
}
public List<List<Integer>> combine(int n, int k) {
combineBackTraking(n, k);
return res;
}
}
4.电话号码的字母组合
- 问题描述:
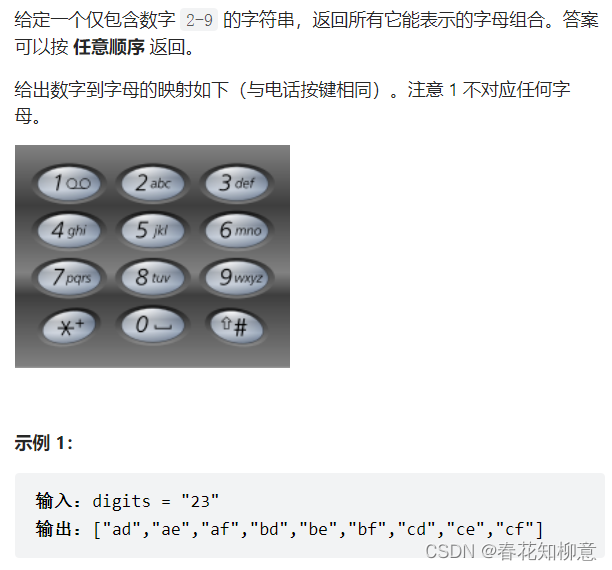
📝 解题思路:
创建字符串数组,存储对应关系
回溯法三部曲:
(1)确定递归函数参数
老样子,将保存字符串集合的变量定义为全局变量;
参数为:字符串digits
(2)确定函数的终止条件
当前结果字符串的长度与原字符串的长度相同
(3)单层遍历逻辑
在循环开始的时候,首先要获得当前数字对应的字符串,遍历这个字符串,将字符添加到StringBuffer保存一个组合的字符串中,然后递归调用回溯函数,深度加一,回退的过程就是删除temp字符串末尾的字符
- Java版本:
class Solution {
List<String> res = new ArrayList<String>();
String [] map = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
StringBuffer temp = new StringBuffer();
public void letter(String digits, int depth){
if(temp.length() == digits.length()){
res.add(temp.toString());
return;
}
String str = map[digits.charAt(depth) - '0'];
for(int i = 0; i < str.length(); i++){
temp.append(str.charAt(i));
letter(digits, depth + 1);
temp.deleteCharAt(temp.length() - 1);
}
}
public List<String> letterCombinations(String digits) {
if(digits.length() == 0){
return res;
}
letter(digits, 0);
return res;
}
}

