?
一、完全背包
题目描述:
题目描述
有个背包可承受重量T,现有N件物品,每件物品重量为Wi,价值为Vi ,每件物品的数量是无穷的,这个背包可以装载物品的最大价值是多少?
输入格式
第一行,两个整数,分别表示T和N,用空格隔开(T≤1000,N≤100)
接下来T行,每行两个整数,分别表示N件物品的重量Wi和价值Vi(1≤Wi,Vi≤100)
输出格式
一行,表示这个背包可以装载物品的最大价值
输入输出样列
输入样例1:
100 5
77 92
22 22
29 87
50 46
99 90🔑思路
完全背包和0-1背包的区别:“物品数量不是1 1个,而是无穷多个”。
那么:
对于物品i来说,最多能装多少个在背包里呢?
背包容量为C,最多能装C/w[i]个物品i。
💯解法
code1转多重背包:
将多重背包中的s[i]定义为C/w[i]进行求解。
过程:
one? 定义状态: d(i,j)表示前i种物品放在承重量为j的背包里可以获得的最大价值。
two? 状态转移方程:
dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);three? 时间复杂度
O(N*C*K)
code2转01-背包:
将每种完全背包物品拆成C/w[i]件物品进行0-1背包的DP。
code3完全背包算法:
定义状态:d (i, j)表示为前i种物品分配j的背包空间,可以获得的最大价值!
建立d(N,C)的表,DP将进行填表操作。
状态转移方程:对于物品i的决策可以分为两大类:
①第i件物品一件也不放:d(i,j)=d(i-1,j)上一行。
②第i种物品至少放一个:
由于至少放入一个,考虑最后一个放入的i物品,其占用w_i的空间,并带来v_i的价值。
由于物品i有无限多个,放入一个以后还是有无限多个,但是背包大小减少了w_i。
问题转换为从前i个物品种选择一些物品放入j-w_i的背包中可以获得的最大价值。
状态转移方程:dp(i,j)=max(dp(i-1,j),d(i,j-w_i)+v_i)
实例:
DP填表
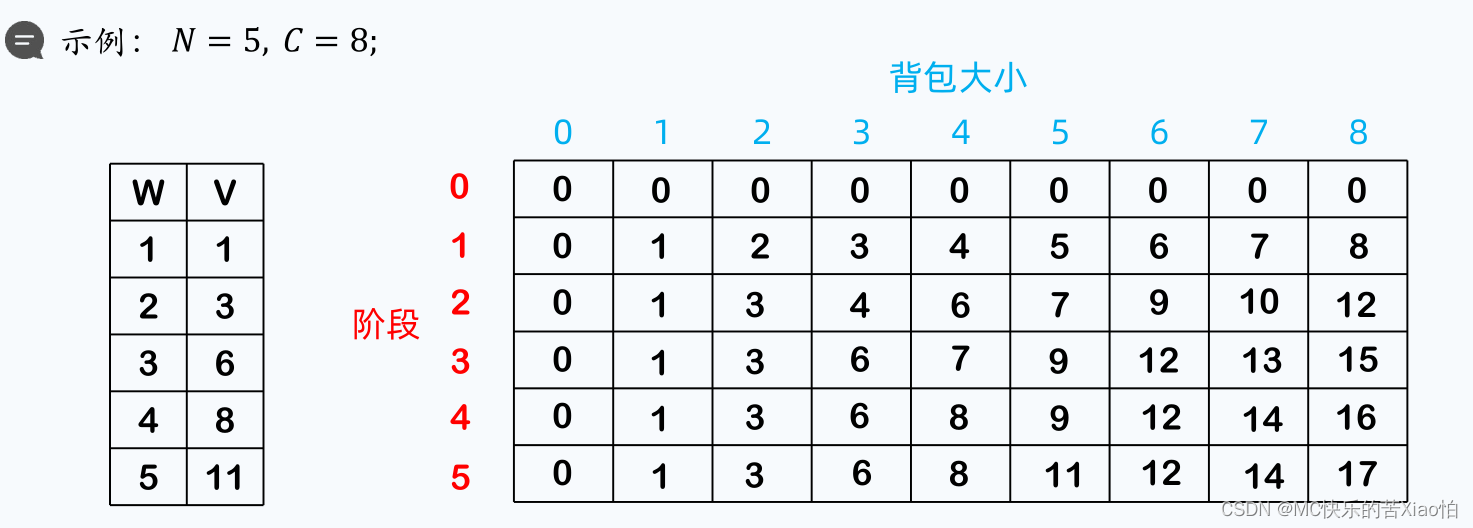
?思考,当前的d(i,j)需要依靠哪些位置:

?由于d(i,j)需要依赖相同行左边的状态,所以i和j的枚举顺序都是从小到大。
再深入思考🤔,能否用滚动数组优化呢?
解决这个问题,我么要想想当前的d(i,j)需要的d(i-1,j)和d(i,j-w_i)是否还保留再一个一维的dp中:
①d(i-1,j) :
还保留在dp中应为当前扫描到d(i,j)的时候d(i-1,j)的值还存储在当前的位置里,还没有改变,所以d(i-1,j)的值可以得到。
②d(i,j-w_i) :
这个不难想到,因为在同一行,d(i,j-w_i)的值还保留在(i,j-w_i)的位置里,前面已经算过了,所以d(i,j-w_i)的值也可以得到。
两个值都可以得到,所以可以滚动数组优化!
💯CODE代码:
code1:转多重背包
#include <bits/stdc++.h>
using namespace std;
const int N=110,C=1010;
int n,c,w[N],v[N],s[N],dp[N][C];
int main()
{
cin>>c>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
for(int k=0;k<=j/w[i];k++)
{
d[i][j]=max(d[i][j],d[i-1][j-k*w[i]]+k*v[[i]]);
}
/*
for(int k=0;k<=c/w[i];k++)
{
if(j>=k*w[i])
{
d[i][j]=max(d[i][j],d[i-1][j-k*w[i]]+k*v[[i]]);
}
}
*/
}
}
cout<<dp[n][c];
return 0;
}
code2:转0-1背包
#include <bits/stdc++.h>
using namespace std;
const int N=110,C=1010,TOT=100010;
int n,c,w[TOT],v[TOT],dp[C],tot,w_i,v_i; //新增一个tot来存储0-1背包中的物品数量,and dp可以滚动数组优化
int main()
{
cin>>c>>n;
for(int i=1;i<=n;i++)
{
cin>>w_i>>v_i;
for(int j=1;j<=c/w_i;j++)
{
w[++tot]=w_i;
v[tot]=v_i;
}
}
for(int i=1;i<=tot;i++){
for(int j=c;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[c];
return 0;
}
code3:完全背包算法
#include <bits/stdc++.h>
using namespace std;
const int N=110,C=1010;
int dp[C],n,c,w[N],v[N];
int main()
{
cin>>c>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(int i=1;i<=n;i++)
{
for(int j=w[i];j<=c;j++)
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout<<dp[t];
return 0;
}二、解决完全背包类问题
例题one
题目描述
卡卡西拿出电脑,列出了条件,很快找到了规律,“第二关,搞定”,铁人老 师不敢相信的看着电脑上的计算数字,狠狠的拍了卡卡西的肩膀,“嘿,你可帮 了大忙了,得好好谢谢你啊!”。“哈哈,不客气,请我吃个冰棍就行啦!”,卡卡 西笑着对老师说,“要不咱们一鼓作气,攻克最后一个难题?”表情明显轻松下 来的铁人老师充满希望的望着卡卡西,“恩,好的,争取快点解决,下午我也可 以早点回家啦”,卡卡西答应了老师。
自行车比赛的赛制本次有所创新,使用共享单车,且每隔一公里都有一个换 乘点,每次换车最多骑行 10 公里,假设按骑行公里数收费,且连续骑行 1 到 10 公里费用不等。一个小朋友要骑行 n 公里,那么怎样换乘共享单车,能使得骑行 n 公里总费用最少呢?
“这个好像有点复杂,不过难不倒我”卡卡西心中给自己加了把劲 ,仔细 计算起来,铁人老师核对了一下,确实没问题,激动地把卡卡西举了起来, “果然解决了,现在所有问题都没了,走,老师给你买雪糕去!”
五一当天,彩旗飞扬,“迷你铁人三项赛”如期举行,有了卡卡西的帮助, 一切都很顺利,卡卡西也满足了自己现场观看比赛的愿望,组委会也给她颁发 了一枚“优秀志愿者”的奖章,卡卡西把它佩戴在胸前,到现在还在闪闪发光 呢。
输入格式
输入文件名:bike.in
输入数据共两行。
第一行为一个正整数 n,表示小朋友要骑行的总路程数。
第二行共十个正整数(中间空格隔开),第 i 个正整数表示 连续骑行 i 公 里的费用 Wi。注意这些数并无实际的经济意义,即骑行 10 公里费用可能 比骑行 1 公里的少。
输出格式
输出文件名:bike.out
仅一个正整数,表示最少的费用
输入输出样列
输入样例1:
18
3 5 9 10 6 20 18 10 30 40
输出样例1:
22
说明
【样例说明】
输入数据第一行 18,表示小朋友要骑行的总路程为 18 公里,输入数 据第二行 10 个数,分别表示连续骑行 1 公里的费用为 3,连续骑行 2 公里的费用为 5,连续骑行 3 公里的费用为 9...以此类推,连续骑行 10 公里的费用为 40。为了骑行总费用最少,可采用的换乘方案是: 先骑行 8 公里,花费为 10;换乘后再骑行 5 公里,花费为 6;换乘后 再骑行 5 公里,花费为 6;总路程为 8+5+5=18 公里,总费用为 10+6+6=22。
【数据范围】
100%的数据:0<Wi<=500,1<=n<=100。🔑思路
问题的目标是要骑行N公里,有 10种骑法,每次骑1公里、2公里......10公里。
将总公里数当成背包、将 10种骑法作为物品,目标就是用 1...10这10个数凑出N N并使得
总消耗最低,由于1...10可以无限次使用,问题可以转换为完全背包问题。定义状态:d(i,j)表示用前i种骑法骑j公里需要的最低花费。答案为f(10,N)。
DP需要全局初始化为极大INF,因为这道题是求min
🆘注意:
当N为0时,方案数为0,如果赋值为INF,会导致推导错误?!
初始化 d(i,0)=0
可以滚动数组优化哦~
核心代码 :
int n=10;
int m;
cin>>m;
for(int i=1;i<=n;i++)
{
cin>>v[i];
}
memset(d,0x3F,sizeof(d));
d[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=i;j<=m;j++)
{
d[j]=min(d[j],d[j-i]+v[i]);
}
}
cout<<d[m];例题two
题目描述
母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统.
他们对货币的数值感到好奇.
传统地,一个货币系统是由 1,5,10,20 或 25,50, 和 100 的单位面值组成的.
母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值.
举例来说, 使用一个货币系统 {1,2,5,10,...}产生 18 单位面值的一些可能的方法是:18x1, 9x2,8x2+2x1, 3x5+2+1,等等其它.
写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值.
保证总数将会适合 long long (C/C++) 和 Int64 (Free Pascal).即在0 到2^63-1之间
输入格式
货币系统中货币的种类数目是 V . (1<= V<=25)
要构造的数量钱是 N . (1<= N<=10,000)
第 1 行: 二个整数, V 和 N
第 2 行: 可用的货币的面值
输出格式
单独的一行,表示那个可能的用这V种货币凑足N单位货币的方案数。
输入输出样列
输入样例1:
3 10
1 2 5
输出样例1:
10🔑思路
问题要求用V种不同面值的货币(每种货币数量不限)凑出刚好N元钱。
将需要凑出的钱数N看做背包大小,问题可以抽象为完全背包方案数问题。
状态转移方程:d(i,j) = d(i-1,j) + d(i,j-w_i); (两种选择的方案数之和)
🆘注意:
当N==0的时候有1种方案,就是不放
初始化:d(i,0)=1
核心代码:
int V,N;
cin>>V>>N;
for(int i=1;i<=V;i++)
{
cin>>a[i];
}
dp[0]=1;
for(int i=1;i<=V;i++)
{
for(int j=a[i];j<=N;j++)
{
dp[j]=dp[j]+dp[j-a[i]];
}
}
cout<<dp[N];
