开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【算法学习】不相交集合数据结构 -> 正文阅读

[数据结构与算法]【算法学习】不相交集合数据结构

参考算法导论第21章用于不相交集合的数据结构

一些应用涉及将 $n$ 个不同的元素分成一组不相交的集合。这些应用经常需要进行两种特别操作：寻找包含给定元素的唯一集合和合并两个集合。这里介绍如何维护一种数据结构来实现这些操作。

（算导21.1节）描述不相交集合数据结构所支持的各种操作，并给出一个简单的应用。
（算导21.2节）使用一种简单链表结构来实现不相交集合。
（算导21.3节）给出一种使用有根树表示的更有效方法。使用树表示的运行时间，理论上超过线性时间 superlinear ，然而对于所有的实际应用它却是线性的。
（算导21.4节）定义并讨论一个增长非常快的函数和其增长极慢的逆函数，这种逆函数应用在「基于树实现上的各种操作」的运行时间中。然后，应用复杂的摊还分析方法，证明一个近似线性运行时间的上界。

1. 不相交集合的操作

一个不相交集合数据结构 disjoint-set data structure 维护了一个不相交动态集的集合 $\{ S_1, S_2, \dots, S_k\}$ 。我们用一个代表 representative 来标识每个集合，它是这个集合的某个成员。在一些应用中，我们不关心哪个成员被用来作为代表，仅仅关心的是：在不修改这些动态集合的前提下，查询一个动态集合的代表两次，我们的这两次查询应该得到相同的答案。其他一些应用可能需要一个预先指定的规则来选择代表，比如选择这个集合中最小的成员（当然，假设集合中的元素能被比较次序）。

如同已经探讨过的动态集合的其他实现，用一个对象表示一个集合中的每个元素 represent each element of a set by an object 。设 $x$ 表示一个对象，我们希望支持以下三个操作：

MAKE-SET(x) ：建立一个新的集合，它的唯一成员（因而为代表）是 $x$ 。因为各个集合是不相交的，故 $x$ 不会出现在别的某个集合中。
UNION(x, y) ：将包含 $x$ 和 $y$ 的两个动态集合（表示为 $S_x$ 和 $S_y$ ）合并成一个新的集合，即这两个集合的并集。假定在操作之前这两个集合是不相交的。虽然 UNION 的许多实现中、特别地选择 $S_x$ 或 $S_y$ 的代表作为新的代表，然而结果集合的代表可以是 $S_x \cup S_y$ 的任何成员。由于我们要求各个集合不相交，故要“消除”原有的集合 $S_x$ 和 $S_y$ ，即把它们从 $S$ 中删除。实际上，我们经常把其中一个集合的元素并入另一个集合中、来代替删除操作。
FIND-SET(x) ：返回一个指针，这个指针指向包含 $x$ 的（唯一）集合的代表。

我们使用两个参数来分析不相交集合数据结构的运行时间：一个参数是 $n$ ，表示 MAKE-SET 操作的次数；另一个是 $m$ ，表示 MAKE-SET, UNION, FIND-SET 操作的总次数。因为各个集合是不相交的，所以每个 UNION 操作减少一个集合。因此，在 $n ? 1$ 次 UNION 操作后，只有一个集合留下来。也就是说，UNION 操作的次数至多是 $n ? 1$ 。也要注意到，由于 MAKE-SET 操作被包含在总操作次数 $m$ 中，因此有 $\ge n$ 。这里我们假设 $n$ 个 MAKE-SET 操作总是最先执行的 $n$ 个操作。

不相交集合数据结构的一个应用

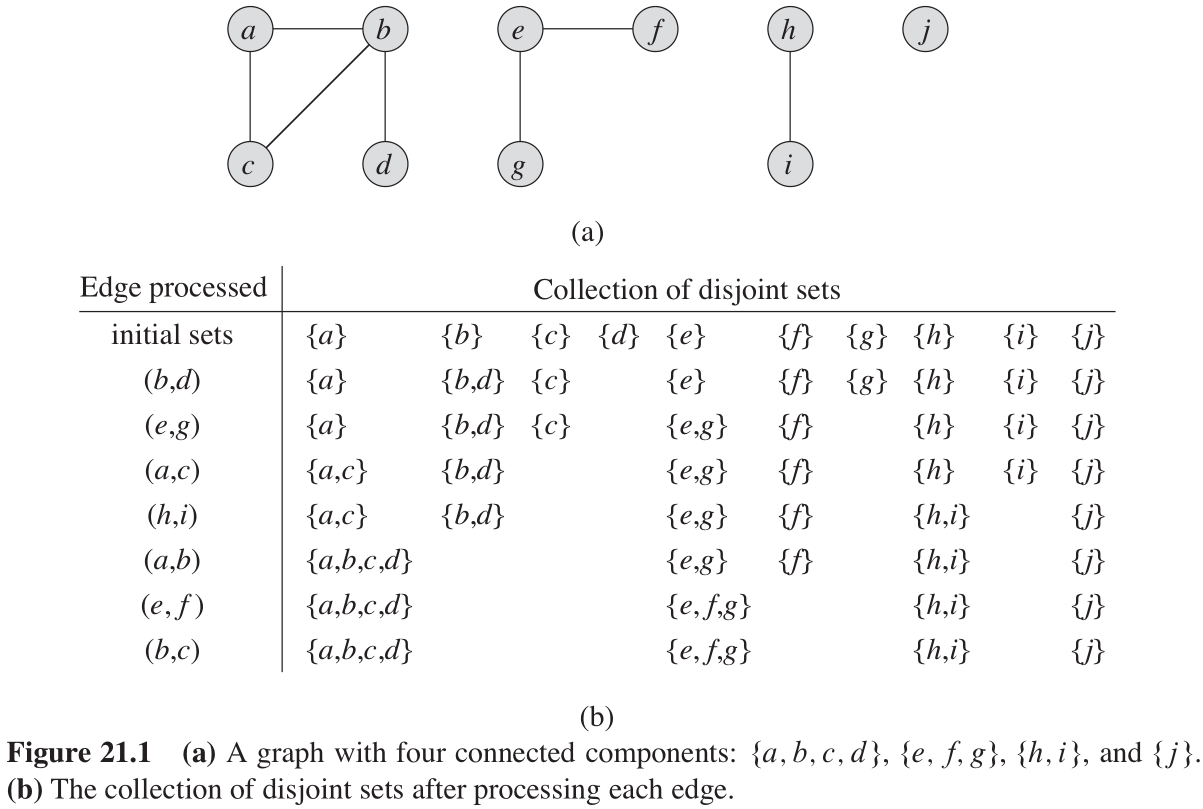
不相交集合数据结构的许多应用之一是，确定无向图的连通分量（算导B.4节）。例如，图21-1(a)显示了一个包含四个连通分量的图。而下面的 CONNECTED-COMPONENTS 过程使用不相交集合操作、来计算一个图的连通分量。一旦 CONNECTED-COMPONENTS 预处理了该图，过程 SAME-COMPONENT 就回答两个顶点是否在同一个连通分量的循环（下面的伪码中，图 $G$ 的顶点集用 $G . V$ 表示，边集用 $G . E$ 表示）。
在这里插入图片描述

CONNECTED-COMPONENTS(G)
	for each vertex v in G.V
		MAKE-SET(v)
	for each edge(u, v) in G.E
		if FIND-SET(u) != FIND-SET(v)
			UNION(u, v)

SAME-COMPONENT(u, v)
	return FIND-SET(u) == FIND-SET(v)

过程 CONNECTED-COMPONENTS 开始时，将每个顶点 $v$ 放在它自己的集合中。然后，对于每条边 $(u, v)$ ，它将包含 $u$ 和 $v$ 的集合进行合并。（由算导练习21.1-2）处理完所有的边之后，两个顶点在相同的连通分量当且仅当与之对应的对象在相同的集合中。因此，CONNECTED-COMPONENTS 以这种方式计算出的集合，使得过程 SAME-COMPONENT 能确定两个顶点是否在相同的连通分量中。图21-1(b)指出了 CONNECTED-COMPONENTS 如何计算不相交集合。

在该连通分量算法的实际实现中，图和不相交集数据结构的表示需要相互引用。也就是说，一个表示顶点的对象会包含一个指向与之对应的不相交集合对象的指针；反之亦然。这些编程细节取决于实现的编程语言，不再赘述。

2. 不相交集合的链表表示

图21-2(a)给出了一个实现不相交集数据结构的简单方法：每个集合用一个它自己的链表来表示 each set is represented by its own linked list 。每个集合对象包含 head 和 tail 属性，head 属性指向链表中的第一个对象，tail 属性指向链表中的最后一个对象。链表中的每个（集合成员）对象都包含一个集合成员、一个指向链表中下一个对象的指针、一个指回到集合对象的指针。在每个链表中，（集合成员）对象可以以任意的次序出现。代表元素是链表中第一个对象的集合成员 The representative is the set member in the first object in the list 。
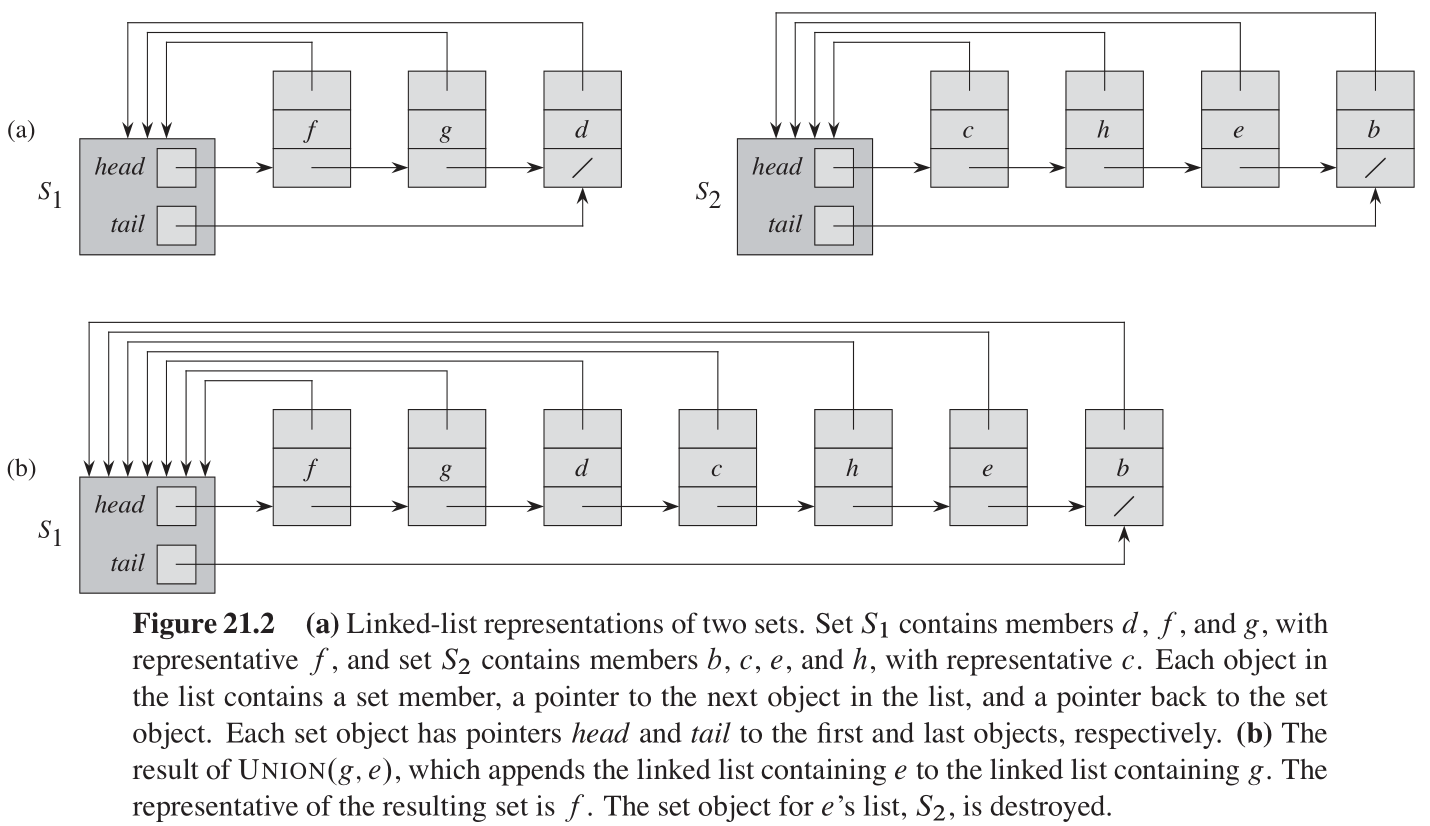
在这里插入图片描述
用这种链表表示，MAKE-SET 操作和 FIND-SET 操作都是非常方便的，只需 $O (1)$ 的时间。要执行 MAKE-SET(x) 操作，我们需要创建一个只有 $x$ 对象的新链表。对于 FIND-SET(x) ，仅沿着 $x$ 对象的返回指针回到它的集合对象，然后返回「 head 指向的对象」中的集合成员 the member in the object that head points to（即代表元素）。例如，在图21-2(a)中，调用 FIND-SET(g) 将返回 f 。

2.1 合并的一个简单实现

在使用链表集合表示的实现中，UNION 操作的最简单实现、明显比 MAKE-SET 或 FIND-SET 花费的时间多。如图21-2(b)所示，我们通过把 $y$ 所在的链表拼接到 $x$ 所在的链表、实现了 UNION(x, y) 。 $x$ 所在链表的代表元素成为结果集的代表元素。我们使用 $x$ 所在链表的 tail 指针，可以迅速地找到在哪里拼接 $y$ 所在链表。因为 $y$ 所在链表的所有成员加入了 $x$ 所在链表中，此时可以删除 $y$ 所在链表的集合对象。遗憾的是，对于 $y$ 所在链表的每个对象，我们必须更新指向集合对象的指针，这要花费的时间与 $y$ 所在链表长度呈线性关系。例如，在图21-2中，UNION(g, e) 促使 b, c, e, h 对象的指针被更新。

事实上，我们能轻松构建一个「在 $n$ 个对象上需要 $\Theta(n^2)$ 时间的 $m$ 个操作」的序列。假设有对象 $x_1, x_2, \dots, x_n$ 。如图21-3所示，执行 $n$ 个 MAKE-SET 操作，后面跟着执行 $n ? 1$ 个 UNION 操作，因为有 $m = 2 n ? 1$ 。执行 $n$ 个 MAKE-SET 操作需要 $\Theta(n)$ 的时间。由于第 $i$ 个 UNION 操作更新 $i$ 个对象，因此所有的 $n ? 1$ 个 UNION 操作更新的对象的总数为： $\sum^{n-1}_{i=1} i = \Theta(n^2)$
在这里插入图片描述
总的操作数为 $2 n ? 1$ ，这样每个操作平均需要 $\Theta(n)$ 的时间。也就是说，一个操作的摊还时间为 $\Theta(n)$ 。

2.2 一种加权合并的启发式策略

在最坏情况下，上面给出的 UNION 过程的每次调用平均需要 $\Theta(n)$ 的时间，这是因为需要把一个较长的表拼接到一个较短的表上，此时必须对较长表的每个成员、更新其指向集合对象的指针。现在换一种做法，假设每个表中还包含了表的长度（这是很容易维护的）、以及拼接次序可以任意，我们总是把较短的表拼接到较长的表中。使用这种简单的加权合并启发式策略 weighted-union heuristic ，如果两个集合都有 $\Omega(n)$ 个成员，则单个的 UNION 操作仍然需要 $\Omega(n)$ 的时间。

然而下面的定理表明，一个具有 $m$ 个 MAKE-SET, UNION, FIND-SET 操作的序列（其中有 $n$ 个是 MAKE-SET 操作）需要耗费 $n\log n)$ 时间。

定理21.1 使用不相交集合的链表表示和加权合并启发式策略，一个具有 $m$ 个 MAKE-SET 、UNION 和 FIND-SET 操作的序列（其中有 $n$ 个是 MAKE-SET 操作）需要的时间为 $n\log n)$ 。
证明：由于每个 UNION 操作合并两个不相交集，因此总共至多执行 $n ? 1$ 个 UNION 操作。现在来确定由这些 UNION 操作所花费的时间的上界。我们先确定「每个对象指向它的集合对象的指针」被更新次数的上界。

考虑某个对象 $x$ ，我们知道每次 $x$ 的指针被更新， $x$ 早先一定在一个规模较小的集合中。因此第一次 $x$ 的指针被更新时，结果集一定至少有 $2$ 个成员。类似地，下次 $x$ 的指针被更新时结果集一定至少有 $4$ 个成员。一直继续下去，注意到对于任意的 $\le n$ ，在 $x$ 的指针被更新 $\lceil \log k \rceil$ 次后，结果集一定至少有 $k$ 个成员。因为最大集合至多包含 $n$ 个成员，故每个对象的指针在所有的 UNION 操作中最多被更新 $\lceil \log n \rceil$ 次。因此，在所有的 UNION 操作中、被更新的对象的指针总数为 $\log n)$ 。当然，我们也必须考虑 tail 指针和表长度的更新，而它们在每个 UNION 操作中只花费 $\Theta(1)$ 时间，所以总共花在 UNION 操作的时间为 $O(n\log n)$ 。

整个具有 $m$ 个操作的序列所需的时间很容易求出。每个 MAKE-SET 和 FIND-SET 操作需要 $O (1)$ 时间，它们的总数为 $O (m)$ 。所以整个序列的总时间为 $\log n)$ 。 $\blacksquare$

3. 不相交集合森林

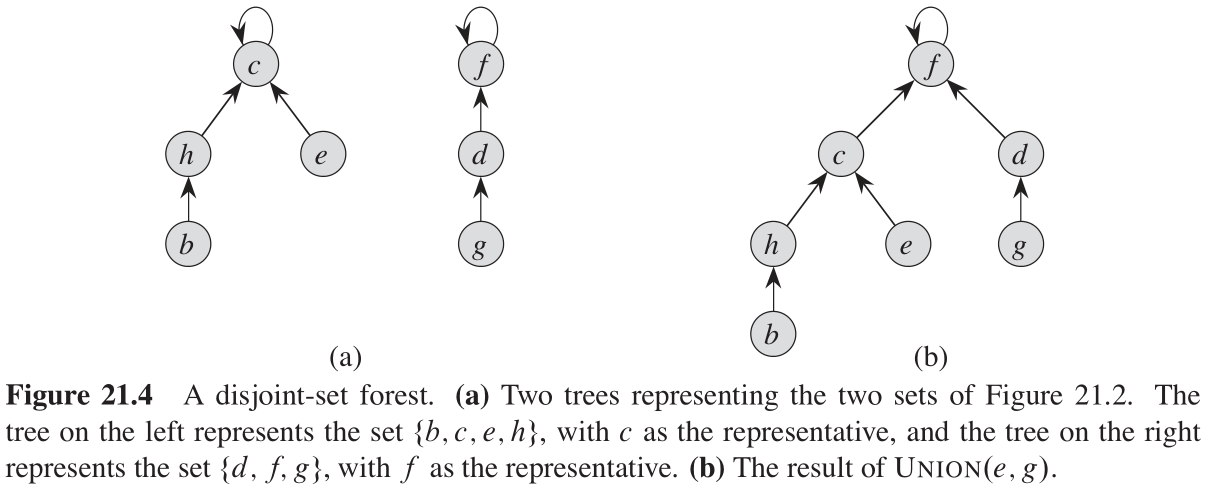
在一个不相交集合更快的实现中，我们使用有根树来表示集合，树中每个结点包含一个成员，每个成员仅指向它的父结点。在一个不相交集合森林 disjoint-set forest 中（如图21-4(a)所示），每棵树代表一个集合，每棵树的根包含集合的代表元素，并且是其自己的父结点。正如我们将要看到的那样，虽然使用这种表示的直接算法并不比使用链表表示的算法快，但通过引入两种启发式策略——按秩合并和路径压缩，我们能得到一个渐近最优的不相交集合数据结构。

我们执行以下三种不相交集合操作：MAKE-SET 操作简单地创建一棵只有一个结点的树，FIND-SET 操作沿着指向父结点的指针、找到树的根，这一通往根结点的简单路径上所访问的结点构成了查找路径 find path 。UNION 操作（如图21-4(b)所示）使得一棵树的根指向另外一棵树的根。
在这里插入图片描述

3.1 改进运行时间的启发式策略

到目前为止，我们还没有对使用链表的实现做出改进。一个包含 $n ? 1$ 个 UNION 操作的序列，可以构造出一棵恰好含有 $n$ 个结点的线性链的树。然而，通过使用两种启发式策略，我们能获得一个几乎与总的操作数 $m$ 呈线性关系的运行时间。

第一种启发式策略是按秩合并 union by rank ，它类似于链表表示中使用的加权合并启发式策略。显而易见的做法是，使具有较少结点的树的根、指向具有较多结点的树的根。不过，我们这里并不显式地记录以每个结点为根的子树的大小 the size of the subtree rooted at each node（即不按大小归并），而是采用一种易于分析的方法（即按高度归并）——对于每个结点，维护一个秩，它表示该结点高度（即到后代叶结点的最长简单路径长度）的一个上界 an upper bound on the height of the node 。在使用按秩合并策略的 UNION 操作中，我们可以让具有较小秩的根指向具有较大秩的根。
第二种启发式策略是路径压缩 path compression ，也相当简单和高效。如图21-5所示，在 FIND-SET 操作中，使用这种策略可以使查找路径中的每个结点直接指向根。路径压缩并不改变任何结点的秩。

3.2 实现不相交集合森林的伪代码

为了使用按秩合并的启发式策略来实现一个不相交集合森林，我们必须记录下秩的变化情况。对于每个结点 $x$ ，维护一个整数值 $x . r a n k$ ，它代表 $x$ 的高度（从 $x$ 到某一后代叶结点的最长简单路径上边的数目）的一个上界。

当 MAKE-SET 创建一个单元素集合 a singleton set 时，对应树中的单个结点有一个为 $0$ 的初始秩。
每个 FIND-SET 操作不改变任何秩。
UNION 操作有两种情况，取决于两棵树的根是否有相同的秩。如果根没有相同的秩，就让较大秩的根成为较小秩的根的父结点，但其秩本身保持不变；否则当两个根有相同的秩时，任意选择两个根中的一个作为父结点，并使它的秩加 $1$ .

下面把这种方法表示成伪码。用 $x . p$ 代表结点 $x$ 的父结点。LINK 过程是由 UNION 调用的一个子过程，以指向两个根的指针作为输入。带有路径压缩的 FIND-SET 过程也非常简单。

MAKE-SET(x)
	x.p = x
	x.rank = 0

UNION(x, y)
	LINK(FIND-SET(x), FIND-SET(y))

LINK(x, y)
	if x.rank > y.rank
		y.p = x
	else x.p = y
		if x.rank == y.rank
			y.rank = y.rank + 1

FIND-SET(x)
	if x != x.p
		x.p = FIND-SET(x, p)
	return x.p

FIND-SET 过程是一种两趟方法 two-pass method ：当它递归时，第一趟沿着查找路径向上、直到找到根。当递归回溯时，第二趟沿着搜索树向下更新每个结点，使其直接指向根。FIND-SET(x) 的每次调用在第三行返回 $x . p$ 。如果 $x$ 是根，则 FIND-SET 跳过第二行并返回 $x . p$ （也就是 $x$ ），这是递归到底的情形。否则，执行第二行，并且参数为 $x . p$ 的递归调用返回一个指向根的指针；第二行更新结点 $x$ 、让其父结点 $x . p$ 直接指向根结点，然后第三行返回这个指针。

3.3 启发式策略对运行时间的影响

如果单独使用按秩合并或路径压缩，它们每个都能改善不相交集合森林上操作的运行时间，而一起使用这两种启发式策略时，这种改善更大。单独来看，按秩合并产生的运行时间为 $O(m\log n)$ （算导练习21.4-4），并且这个界是紧的（算导练习21.3-3）。对于一个具有 $n$ 个 MAKE-SET 操作（因此最多有 $n ? 1$ 个 UNION 操作）和 $f$ 个 FIND-SET 操作的序列，单独使用路径压缩启发式策略，给出的最坏情况运行时间为 $\Theta(n + f \cdot (1 + \log_{2+ f / n } n))$ 。

当同时使用按秩合并和路径压缩时，最坏情况的运行时间为 ${\alpha} (n))$ ，这里 $\alpha(n)$ 是一个增长非常慢的函数，其定义在第四节给出。在任何一个可以想得到的不相交集合数据结构的应用中，都有 $\alpha(n) \le 4$ ；因此，我们可以认为在所有实际应用中，其运行时间与 $m$ 呈线性关系。然而严格来说，它是超线性的。下面将证明这个上界。

4. 带路径压缩的按秩合并的分析

如第三节（算导21.3节）提到的，对于 $n$ 个元素上的 $m$ 个不相交集合操作，联合使用按秩合并与路径压缩启发式策略后的运行时间是 $\alpha (n))$ 。本节中将考察 $\alpha$ 函数，看看 $\alpha$ 函数增长到底有多慢，然后使用摊还分析中的势方法来证明这一运行时间。

4.1 一个增长非常快的函数与其增长非常慢的逆函数

对于整数 $\ge 0$ 与 $\ge 1$ ，定义函数 $A_k (j)$ 为： $A_k (j) = \begin{cases} j + 1 \quad &如果k =0 \\ A^{ (j +1) } _{k - 1} (j ) \quad &如果k \ge 1 \end{cases}$ 其中表达式 $A^{ (j+1) }_{k-1} (j)$ 采用了（算导3.2节给出的）函数迭代记号。具体来说，对 $\ge 1$ 有 $\begin{aligned} &A^{ (0) }_{k-1}(j) = j\\ &A_{k-1} ^{ (i) } (j) = A_{k - 1} ( A_{k-1} ^{ (i - 1 ) } (j) )\end{aligned}$ 我们称参数 $k$ 为函数 $A$ 的级 level 。

函数 $A_k(j)$ 随着 $j$ 和 $k$ 严格递增。为了了解该函数增长有多快，先要得到 $A_1(j)$ 和 $A_2(j)$ 的闭形式表示 closed-form expressions 。

引理21.2 对于任意整数 $\ge 1$ ，有 $A_1(j)= 2j + 1$ 。
证明：先对 $i$ 使用归纳法来证明 $A_0^{(i)} (j) = j + i$ 。对于归纳基础，有 $A_0^{ (0) } (j) = j = j +0$ 。对于归纳步，假设 $A_0 ^{ (i-1) } (j) = j + (i - 1)$ 。然后 $A_0^{ (i) } (j)= A_0 (A_0^{(i-1)} (j)) = (j + (i - 1)) + 1 = j + i$ 。最后，我们有 $A_1 (j) = A_0^{ (j+1) } (j) = j + (j+1) = 2j + 1$ 。 $\blacksquare$

引理21.3 对于任意整数 $\ge 1$ ，有 $A_2(j)= 2^{j + 1} (j + 1)- 1$ 。
证明：先对 $i$ 使用归纳法来证明 $A_1^{ (i) } (j) = 2^i (j + 1) - 1$ 。对于归纳基础，有 $A_1^{ (0) } (j) = j = 2^0 (j +1) - 1$ 。对于归纳步，假设 $A_1^{ (i-1) } (j) = 2^{i-1} (j + 1) - 1$ 。然后 $A_1^{(i)} (j) = A_1 (A_1^{(i-1)} (j)) = A_1 (2^{i-1} (j+1) - 1) = 2\cdot (2^{i-1} (j + 1) - 1) + 1 = 2^i(j+1) - 2+1 = 2^i(j+1) - 1$ 。最后，我们有 $A_2(j) = A_1^{(j+1)} (j) = 2^{j + 1} (j+1 ) - 1$ 。 $\blacksquare$

现在对于级 $k = 0, 1, 2, 3, 4$ ，我们简单地考察 $A_k(1)$ 就能看到 $A_k(j)$ 增长得有多快了。根据 $A_0(k)$ 的定义、以及上面的引理，有 $A_0(1) = 1+1 = 2,\ A_1(1) = 2 \cdot 1 + 1 = 3,\ A_2(1) = 2^{1+1} \cdot (1 + 1) - 1 =7$ 。我们同样有： $A_3 (1) = A_2^{(2)} (1) = A_2 (A_2 (1)) =A_2(7)=2^8 \cdot 8 - 1 = 2^{11} - 1 = 2047$

并且有： $A_4(1) = A_3^{(2) } (1) = A_3 (A_3(1)) = A_3 (2047) = A_2^{(2048)} (2047) >> \\{} \\ A_2(2047) = 2^{2048} \cdot 2048 - 1 > 2^{2048} = (2^4)^{512} = 16^{512} >> 10^{80}$ $10^{80}$ 就是客观宇宙中所有原子的估计数目。

对于整数 $\ge 0$ ，我们定义函数 $A_k(n)$ 的逆函数如下：
$\alpha(n) = \min \{ k \mid A_k (1) \ge n \}$

也就是说， $\alpha(n)$ 是满足 $A_k(1)$ 至少为 $n$ 的最小的级 $k$ 。根据上面的 $A_k(1)$ 值，可以知道： $\alpha(n) = \begin{cases} 0 \quad &对0 \le n \le 2 \\ 1 \quad &对 n = 3 \\ 2 \quad &对 4 \le n \le 7 \\ 3 \quad &对 8 \le n \le 2047 \\ 4 \quad &对2048 \le n \le A_4 (1) \end{cases}$ 只有对于那些非常大的“天文数字”的 $n$ 值（比 $A_4(1)$ 还大的值，一个巨大的数），才会有 $\alpha(n) > 4$ ，所以对于所有实际的应用，都有 $\alpha(n) \le 4$ 。

4.2 秩的性质

在剩下的部分，我们证明使用按秩合并和路径压缩启发式策略的、不相交集合操作的运行时间界为 $\alpha(n))$ 。为了证明这个界，首先证明秩的一些简单性质。

引理21.4 对于所有的结点 $x$ ，有 $\le x.p.rank$ ，如果 $\ne x.p$ ，则此式是严格不等式。 $x . r a n k$ 的初始值为 $0$ ，并且随时间而增加，直到 $\ne x.p$ ；从此以后， $x . r a n k$ 的值就不再发生变化。 $x . p . r a n k$ 的值随时间单调递增。
证明：使用（算导21.3节中）MAKE-SET, UNION, FIND-SET 的实现，对操作数使用归纳法，其证明是直接的（算导练习21.4-1）。 $\blacksquare$

推论21.5 从任何一个结点指向根的简单路径上，结点的秩是严格递增的。 $\blacksquare$

引理21.6 每个结点的秩最大为 $n ? 1$ 。
证明：每个结点的秩从 $0$ 开始，并且只有执行了 LINK 操作，它才会增加。因为最多有 $n ? 1$ 个 UNION 操作，所以同样最多有 $n ? 1$ 个 LINK 操作。因为每个 LINK 操作或者不改变任何的秩、或者将某结点的秩加 $1$ ，所以所有的秩最大为 $n ? 1$ 。 $\blacksquare$

引理21.6提供了一个关于结点秩的较弱的界。事实上，每个结点的秩最大为 $\lfloor \log n \rfloor$ （算导练习21.4-2）。然而，引理21.6的这个较松的界已足够满足我们的要求。

4.3 时间界的证明

我们将利用摊还分析中的势方法（算导17.3节）来证明 $O(m\alpha (n))$ 的时间界。在进行摊还分析时，为了方便起见，我们假设不调用 UNION 操作、而是调用 LINK 操作。也就是说，因为 LINK 过程的参数是指向两个根的指针，故我们的行为就像是分别执行适当的 FIND-SET 操作。下面的引理说明，即使因调用 UNION 而导致额外的 FIND-SET 操作，其渐近运行时间仍然保持不变。

引理21.7 假设通过将每个 UNION 转换成两个 FIND-SET 操作、后再接一个 LINK 操作，我们可以把 $m^{'}$ 个 MAKE-SET, UNION, FIND-SET 操作的序列 $S^{'}$ 转换成 $m$ 个 MAKE-SET, LINK, FIND-SET 操作的序列 $S$ 。那么，如果操作序列 $S$ 的运行时间为 $\alpha( n))$ ，则序列 $S^{'}$ 的运行时间为 $\alpha (n))$ 。
证明：由于序列 $S^{'}$ 中的每个 UNION 操作被转换成 $S$ 中的三个操作，于是有 $\le m \le 3m'$ 。因为 $m = O (m^{'})$ ，所以如果转换后的序列 $S$ 的时间界为 $\alpha (n))$ ，就蕴含着原序列 $S^{'}$ 的时间界为 $\alpha( n))$ （？）。 $\blacksquare$

在本节剩下的部分，假设 $m^{'}$ 个 MAKE-SET, UNION, FIND-SET 操作的初始序列，被转换为 $m$ 个 MAKE-SET, LINK, FIND-SET 操作的序列。现在证明，转换后的序列的运行时间界为 $\alpha (n))$ ，并且应用引理21.7证明， $m^{'}$ 个操作的初始序列的运行时间界为 $\alpha(n))$ 。

4.4 势函数

我们使用的势函数在 $q$ 个操作之后，对不相交集合森林中的每个结点 $x$ 都指派了一个势 $\phi_q(x)$ 。把所有的结点的势加起来、就得到了整个森林的势： $\displaystyle \Phi_q = \sum_x \phi_q(x)$ 。其中 $\Phi_q$ 代表 $q$ 次操作之后森林的势。在第一次操作之前，森林是空的，任意置 $\Phi_q = 0$ 。势 $\Phi_q$ 从来不为负值。

$\phi_q(x)$ 的值取决于在第 $q$ 次操作之后， $x$ 是否是一棵树的根。如果是或者如果 $x . r a n k = 0$ ，那么 $\phi_q(x) = \alpha(n) \cdot x.rank$ 。现在假定第 $q$ 次操作之后， $x$ 不是一个树根且 $\ge 1$ 。此时在定义 $\phi_q(x)$ 之前，需要定义两个关于 $x$ 的辅助函数。先定义： $\max \{ k \mid x.p.rank \ge A_k (x.rank) \}$

也就是说， $l e v e l (x)$ 是 $A_k(x.rank)$ （即作用于 $x$ 的秩的函数）的一个最大级 $k$ ，并且 $A_k(x.rank)$ 不大于 $x$ 的父结点的秩。

我们断言： $\le level(x) < \alpha(n) \tag{21.1}$

成立。它可以如下推出： $\begin{aligned} x.p.rank &\ge x.rank + 1 \quad &根据引理21.4 \\ &= A_0 (x.rank) \quad &根据A_0(j)的定义\end{aligned}$ 这意味着 $\ge 0$ ，并且有：
$\begin{aligned} A_{ \alpha(n) } (x.rank)& \ge A_{\alpha(n) } (1) \quad &因为A_k(j)是严格递增的 \\ &\ge n \quad &根据\alpha(n)的定义 \\ &> x.p.rank \quad &根据引理21.6 \end{aligned}$ 这意味着 $\alpha(n)$ 。注意到，由于 $x . p . r a n k$ 是随时间单调递增的，这样 $l e v e l (x)$ 也随时间单调递增。

当 $\ge 1$ 时，第二个辅助函数是： $\max \{ i \mid x.p.rank \ge A_{ level(x) } ^{(i)} (x.rank) \}$ 也就是说， $i t e r (x)$ 是可以迭代地实施 $A_{ level(x) }$ 的最大次数，开始时将 $A_{ level(x)}$ 应用于 $x$ 的秩，直到在获得一个大于「 $x$ 的父结点的秩」的值之前、迭代停止。

当 $\ge 1$ 时，我们有： $\le iter(x) \le x.rank \tag{21.2}$ 成立，它可以如下推出：
$\begin{aligned} x.p.rank &\ge A_{level(x)} (x.rank) \quad&根据level(x)的定义 \\ &= A_{ level(x) }^{ (1) } (x.rank) \quad &根据函数迭代的定义 \end{aligned}$ 这意味着 $\ge 1$ ，并且有： $\begin{aligned} A^{ (x.rank +1) } _{level(x) } (x.rank) &= A_{level(x) + 1} (x.rank) \quad &根据A_k(j)的定义 \\ &> x.p.rank \quad &根据 level(x)的定义 \end{aligned}$ 这意味着 $\le x.rank$ 。注意到，由于 $x . p . r a n k$ 是随时间单调递增的，为了使 $i t e r (x)$ 能够减小， $l e v e l (x)$ 必须增加。只要 $l e v e l (x)$ 保持不变， $i t e r (x)$ 一定是增加或者保持不变。

使用本处定义的这些辅助函数，就可以来定义 $q$ 次操作之后结点 $x$ 的势：
$\phi_q(x) = \begin{cases} \alpha(n) \cdot x.rank \quad &如果x是一个树根或x.rank = 0 \\ ( \alpha(n) - level(x)) \cdot x.rank - iter(x) \quad &如果x不是一个树根并且x.rank \ge 1 \\ \end{cases}$

接下来给出结点势的一些有用的性质。

引理21.8 对于每个结点 $x$ 和所有操作的计数 $q$ ，我们有：
$\le \phi_q(x ) \le \alpha( n) \cdot x.rank$

证明：如果 $x$ 是一个树根或者 $x . r a n k = 0$ ，那么根据定义，有 $\phi_q(x) = \alpha(n) \cdot x.rank$ 。现在假设 $x$ 不是一个树根且 $\ge 1$ 。通过最大化 $l e v e l (x)$ 和 $i t e r (x)$ 来得到 $\phi_q(x)$ 的一个下界。根据界 $(21.1)$ ，有 $level(x)\le \alpha(n)- 1$ ；并且根据界 $(21.2)$ ，有 $\le x.rank$ 。所以有： $\begin{aligned} \phi_q(x) &= ( \alpha(n) - level(x)) \cdot x.rank - iter(x)\\ &\ge ( \alpha(n) - ( \alpha(n) - 1) ) \cdot x.rank - x.rank = x.rank - x.rank = 0\end{aligned}$ 类似地，通过最小化 $l e v e l (x)$ 和 $i t e r (x)$ 来获得 $\phi_q(x)$ 的一个上界。根据界 $(21.1)$ ，有 $\ge 0$ ；并且根据界 $(21.2)$ ，有 $\ge 1$ ，所以有： $\phi_q(x) \le ( \alpha(n) - 0) \cdot x.rank - 1 = \alpha(n) \cdot x.rank - 1 < \alpha(n) \cdot x.rank \qquad \qquad \blacksquare$

推论21.9 如果结点 $x$ 不是一个根结点，并且 $x . r a n k > 0$ ，则 $\phi_q(x) < \alpha(n) \cdot x.rank$ 。 $\blacksquare$

4.5 势的变化与操作的摊还代价

现在，我们准备来分析不相交集合操作是如何影响结点的势的。理解了每个操作引起的势的变化，就能确定每个操作的摊还代价。

引理21.10 设 $x$ 是一个非根结点，并且假设第 $q$ 个操作是 LINK 或 FIND-SET 。那么在第 $q$ 次操作之后， $\phi_q(x) \le \phi_{q - 1}(x)$ 。此外，如果 $\ge 1$ ，并且 $l e v e l (x)$ 或 $i t e r (x)$ 是由于第 $q$ 次操作而发生了改变，那么 $\phi_q(x) \le \phi_{q - 1}(x) - 1$ 。也就是说， $x$ 的势不可能增加，并且如果它有正的势，同时 $l e v e l (x)$ 或者 $i t e r (x)$ 发生改变，则 $x$ 的势至少下降 $1$ 。
证明：因为 $x$ 不是一个树根，所以第 $q$ 个操作并不改变 $x$ 的秩，又因为在前 $n$ 次 MAKE-SET 操作后， $n$ 并不发生改变，所以 $\alpha(n)$ 也同样不发生变化。因此在第 $q$ 个操作后， $x$ 的势公式的这些成分保持相同。如果 $x . r a n k = 0$ ，那么 $\phi_q(x) = \phi_{q-1} (x) = 0$ 。现在假设 $\ge 1$ 。

前面说过， $l e v e l (x)$ 随时间单调递增。如果第 $q$ 个操作使得 $l e v e l (x)$ 不发生改变，那么 $i t e r (x)$ 或者增加、或者保持不变。如果 $l e v e l (x)$ 和 $i t e r (x)$ 都不变，则 $\phi_q(x)= \phi_{q-1}(x)$ 。如果 $l e v e l (x)$ 没有变化，而 $i t e r (x)$ 增加了，则它至少增加 $1$ ，因而有 $\phi_q(x) \le \phi_{q-1} (x)- 1$ 。

最后，如果第 $q$ 个操作增加 $l e v e l (x)$ 的值，并且至少增加 $1$ ，那么 $(\alpha(n) - level(x)) \cdot x.rank$ 的值至少下降 $x . r a n k$ 。因为 $l e v e l (x)$ 的值增加了， $i t e r (x)$ 的值可能下降，但是根据界 $(21.2)$ ，下降最多只有 $x . r a n k ? 1$ 。于是，由 $i t e r (x)$ 的改变导致的势的增加量，少于由 $l e v e l (x)$ 的改变导致的势的减少量，因此可以得出结论： $\phi_q(x) \le \phi_{q-1} (x) -1$ 。 $\blacksquare$

下面的三个引理说明，每个 MAKE-SET, LINK, FIND-SET 的操作的摊还代价都是 $O(\alpha (n))$ 。回顾公式 $(17.2)$ 可知，每个操作的摊还代价是它的实际成本加上操作本身导致的势的增量。

引理21.11 每个 MAKE-SET 操作的摊还代价是 $O (1)$ 。
证明：假设第 $q$ 个操作是 MAKE-SET(x) ，这个操作创建秩为 $0$ 的结点 $x$ ，并使得 $\phi_q(x) = 0$ 。由于没有其他的秩或势的改变，所以 $\Phi_q = \Phi_{q-1}$ 。注意到，MAKE-SET 操作的实际成本是 $O (1)$ ，从而本定理得证。 $\blacksquare$

引理21.12 每个 LINK 操作的摊还代价为 $O(\alpha(n))$ 。
证明：假设第 $q$ 个操作是 LINK(x, y) 。LINK 操作的实际成本为 $O (1)$ 。不失一般性，假设这个 LINK 使 $y$ 成为 $x$ 的父结点。

为了确定 LINK 所导致的势的改变，我们注意到，势可能改变的结点只有 $x$ 、 $y$ 和操作前 $y$ 的子结点。下面证明，由于 LINK 导致的势增加的唯一结点是 $y$ ，并且它的增量最多为 $\alpha(n)$ ：

根据引理21.10，对于那些在 LINK 操作之前为 $y$ 的孩子的任何一个结点，其势都不会因为 LINK 操作而增加。
根据 $\phi_q(x)$ 的定义可知，由于 $x$ 是第 $q$ 次操作之前的一个根， $\phi_{q-1} (x) = \alpha(n)\cdot x.rank$ 。如果 $x . r a n k = 0$ ，那么 $\phi_q(x) = \phi_{q-1} (x) = 0$ ；否则， $\begin{aligned}\phi_q(x) &< \alpha(n) \cdot x.rank \quad 根据推论21.9 \\ &= \phi_{q-1}(x)\end{aligned}$ 所以 $x$ 的势减小了。
因为 $y$ 在这个 LINK 操作之前是一个根，所以 $\phi_{q - 1}(x) = \alpha(n)\cdot x.rank$ 。这个 LINK 操作使得 $y$ 成为一个根，并且它使得 $y$ 的秩不变或增加 $1$ 。因此 $\phi_q(y) = \phi_{q-1}(y)$ 或 $\phi_q(y) = \phi_{q-1}(y) + \alpha(n)$ 。

因此，由于这个 LINK 操作导致势至多增加 $\alpha(n)$ ，所以这个 LINK 操作的摊还代价是 $\alpha(n) = O(\alpha(n))$ 。 $\blacksquare$

引理21.13 每个 FIND-SET 操作的摊还代价为 $O(\alpha(n))$ 。
证明：假设第 $q$ 个操作是 FIND-SET ，并且查找路径包含 $s$ 个结点。这个 FIND-SET 操作的实际成本为 $O (s)$ 。下面将要证明，由于执行 FIND-SET 操作，没有结点的势会增加，并且在查找路径上最少有 $\max(0, s - ( \alpha (n) + 2))$ 个结点自身的势至少减少 $1$ 。

为了证明没有结点的势会增加，首先对除根以外的所有结点应用引理21.10。然后，如果 $x$ 是根，那么它的势是 $\alpha(n) \cdot x.rank$ ，其值不变。

现在证明，至少有 $\max (0, s - ( \alpha(n) + 2))$ 个结点的势至少下降 $1$ 。假设 $x$ 是查找路径上一个满足 $x . r a n k > 0$ 的结点，且在查找路径上的某处， $x$ 后跟某一个非根结点 $y$ ，它在 FIND-SET 操作之前有 $l e v e l (y) = l e v e l (x)$ （注意在查找路径上， $y$ 不需要紧跟在结点 $x$ 的后面）。在查找路径上，除了至多 $\alpha(n)+2$ 个结点以外，其他所有结点都满足关于 $x$ 的限制。那些不满足限制的是查找路径上的第一个结点（因为它的秩为 $0$ ）、最后一个结点（因为它是根）和路径上最后一个满足 $l e v e l (w) = k$ 的结点，这里 $\dots, \alpha(n) - 1$ 。

让我们固定这样一个结点 $x$ ，下面证明 $x$ 的势至少下降 $1$ 。假设 $k = l e v e l (x) = l e v e l (y)$ 。在由 FIND-SET 操作引起路径压缩之前，我们有： $\begin{aligned} x.p.rank &\ge A_k^{ (iter(x)) } (x.rank) \quad &根据iter(x)的定义 \\ y.p.rank &\ge A_k(y.rank) \quad &根据level(y)的定义 \\ y.rank &\ge x.p.rank \quad &根据推论21.5,并因为在查找路径上y跟在x的后面 \end{aligned}$

将这些不等式组合在一起，并设 $i$ 为路径压缩前 $i t e r (x)$ 的值，我们有： $\begin{aligned} y.p.rank &\ge A_k (y.rank) \\ &\ge A_k (x.p.rank) \quad &因为A_k(j)是严格递增的 \\ &\ge A_k (A_k^{ (iter(x)) } (x.rank)) \\ &= A^{ (i +1)} _k (x.rank) \end{aligned}$

因为路径压缩将使得 $x$ 与 $y$ 有相同的父结点，那么在路径压缩之后，有 $x . p . r a n k = y . p . r a n k$ ，并且路径压缩并不减少 $y . p . r a n k$ 。因为 $x . r a n k$ 并没有改变，在路径压缩之后就有 $\ge A_k^{ (i+1) } (x.rank)$ 。因此，路径压缩将致使 $i t e r (x)$ 增加（至少增加到 $i + 1$ ）或致使 $l e v e l (x)$ 增加（当 $i t e r (x)$ 至少增加到 $x . r a n k + 1$ 时才发生）。不管发生哪种情况，根据引理21.10，有 $\phi_q(x) \le \phi_{q-1}(x) - 1$ 。所以 $x$ 的势至少下降 $1$ 。

FIND-SET 操作的摊还代价是实际成本加上势的改变量。实际成本为 $O (s)$ ，并且我们已经证明势总共下降了至少 $\max (0, s - ( \alpha(n) + 2))$ 。因此，摊还代价最多为 $\alpha (n)+ 2)) = O(s) - s + O( \alpha(n)) = O(\alpha(n))$ ，后面等式是因为我们能放大势的单位、去消除在 $O (s)$ 中包含的内部常量。 $\blacksquare$

把上面的引理综合在一起，就可以产生下面的定理。

定理21.14 一组 $m$ 个 MAKE-SET, UNION, FIND-SET 操作的序列，其中 $n$ 个是 MAKE-SET 操作，它能在一个不相交集合森林上使用按秩合并与路径压缩、在最坏情况时间 $\alpha(n))$ 内处理完。
证明：根据引理21.7、引理21.11、引理21.12、引理21.13，即可得证。 $\blacksquare$