目录
💓第一题 P2524 Uim的情人节礼物·其之弐
记录 prev_permutation 和 next_permutation + 康托展开💒题目描述
🌟解题报告
看到这个数据范围,我的想法其实是直接暴力的。
因为题目需要的是确定当前的序列是第几个最小的,那么可以从当前的序列开始,去找它的前一个比它小的序列,直到找不到为止,因此就可以考虑使用STL中prev_permutation来实现。
关于prev_permutation和next_permutation而言,两者都是找全排列的,细节上不同:
prev_permutation找的是比当前序列的字典序小的上一个序列,直到找不到为止,比如当前的这个问题:
{231}的上一个序列是{213};
{213}的上一个序列是{132};
{132}的上一个序列是{123},到了{123}这里了,也没有比它的字典序更小的序列了,函数就停止了。
next_permutation找的是比当前序列字典序大的下一个序列,直到找不到为止,比如对于当前这个问题:
{231}的下一个序列是{312};
{312}的下一个序列是{321};
我自己想到的是直接暴力,倒是我看到题解很多都是说的康托展开,也没有学过这个东西,现学一下吧🌻参考代码(C++版本)
解法一:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
int a[10];
int main()
{
cin >> n;
int cnt = 1;
//可以使用字符的方式存储
// for(int i = 0; i < n;i++)
// {
// char tmp;
// cin >> tmp;
// a[i] = tmp - '0';
// }
//也可以就使用常规的存储方式,然后反转
int x;
cin >> x;
int i = 0;
int xx = x;
while(xx)
{
a[i++] = xx % 10;
xx /= 10;
}
//反转
reverse(a,a+n);
while(prev_permutation(a,a+n)) cnt++;
cout << cnt<< endl;
return 0;
}
解法二:
康托展开的定义好像挺晦涩的,
直接放它的作用吧:
康托展开的作用是求n个数的全排列中某一个序列在所有排列中的次序(该排列次序(亦称之为排名)以字典序从小到大排序)。
那么现在就只用考虑,怎么实现这个康拓展开的计算式了。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int fac[]={1,1,2,6,24,120,720,5040,40320,362880};//定义康托展开函数中的阶乘
char s[32];
int n;
int Contor(char s[],int n)
{
int ans=0;
for(int i = 0;i < n;i++)
{
int smaller=0;//统计当前位置的右侧的数据中,比当前位置的数据小的个数
for(int j= i+1 ;j<n;j++)
if(s[i] > s[j])smaller++;
//带入康拓展开计算式
ans += smaller*fac[n-i-1];
}
return ans+1;
}
int main()
{
cin>>n;
cin>>s;
cout<<Contor(s,n);
return 0;
}

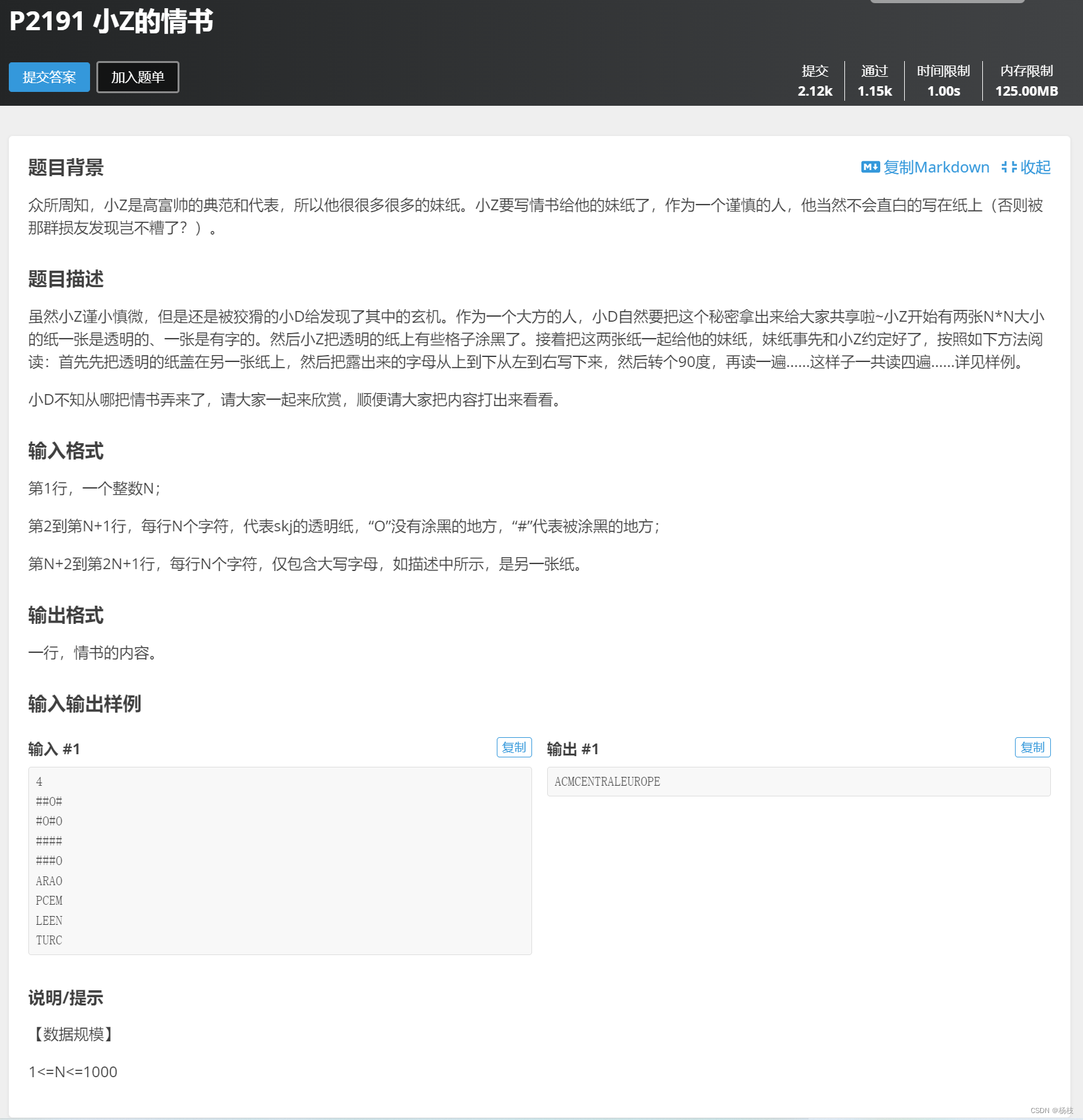
💓第二题 P2191 小Z的情书
💒题目描述
🌟解题报告
这个题,好像是可爱大水题了~
直接按照题目要求,进行模拟,题目要我们输入,那我们就输入,要我们转90度,我们就按照要求转换90度就好。🌻参考代码(C++版本)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010;
char g_paper[N][N],g_word[N][N],g_tmp[N][N];
//模拟旋转
void swapSt(char g_paper[N][N],int n)
{
for(int i = 0; i < n;i++)
for(int j = 0; j < n;j++)
g_tmp[j][n-i-1] = g_paper[i][j];
for(int i = 0; i <n;i++)
for(int j = 0; j < n; j++)
g_paper[i][j] = g_tmp[i][j];
}
//常规的模拟
int main()
{
int n;
cin>>n;
//输入透明纸的状态
for(int i = 0; i < n;i++)
for(int j = 0; j < n;j++)
cin >> g_paper[i][j];
//输入字母表
for(int i = 0; i < n;i++)
for(int j = 0; j < n;j++)
cin >> g_word[i][j];
//枚举四次转换+统计结果
for(int i = 0; i < 4; i++)
{
for(int j = 0; j <n;j++)
for(int k = 0; k < n;k++)
if(g_paper[j][k] == 'O') cout << g_word[j][k];
//90度抓换
swapSt(g_paper,n);
}
return 0;
}

💓第三题 700. 二叉搜索树中的搜索
💒题目描述
🌟解题报告
利用搜索二叉树的性质:
左子树的所有结点数值都小于根结点的数值
右子树的所有结点数值都大于根节点的数值
那么,整体来说,遇到相同就按照题目要求,返回这个结点以及其带的子树,假如是没有搜索到根据当前的val和根节点的root->val做比较,大于根节点信息,递归进右子树查找,否则递归进左子树了。🌻参考代码(C++版本)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
//根据二叉树的性质来吧
//特使情况处理
if(root == nullptr) return nullptr;
//返回结果
if(root->val == val) return root;
//递归进去继续找
return (val < root->val ? searchBST(root->left,val):searchBST(root->right,val));
}
};

💓第四题 230. 二叉搜索树中第K小的元素
二叉搜索树(BST)的中序遍历是升序的💒题目描述
🌟解题报告
二叉搜索树(BST)的中序遍历是有序的是搜索二叉树问题中的核心,题目要求 BST 中第 k 小的元素,等价于求按照中序遍历走,判断当前的这个根是不是第k个元素了。
先序、中序、后序遍历方式的区别是在于把具体的执行操作放在两个递归函数的位置的不同。
对于递归而言,我们需要着重理解的其实是两个部分:决定递归结束的基线条件+执行具体逻辑的部分。那么,套在我们这个题上,我们递归结束的条件是判断传入递归函数的根节点是否还存在,具体执行的逻辑了,是判断当前的结点是否是第k个,倘若是就记录答案。
只是这个题是放在一个中序遍历的背景下进行的,因为二叉树搜索树是左子树中的数据最小,其次是当前的根,最后是右子树中的信息。
所以就需要先递归进左子树,再执行判断当前的结点是否满足要求,再递归进右子树。至于递归进左子树以及递归进右子树的,也是按照同样的逻辑,判断当前结点是否存在,再判断当前的结果是不是第k小的。🌻参考代码(C++版本)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int ans = -1;
void dfs(TreeNode* root, int &k)
{
if(!root) return;
dfs(root->left,k);
k --;
if(k == 0) ans = root->val;
dfs(root->right,k);
}
int kthSmallest(TreeNode* root, int k) {
dfs(root,k);
return ans;
}
};

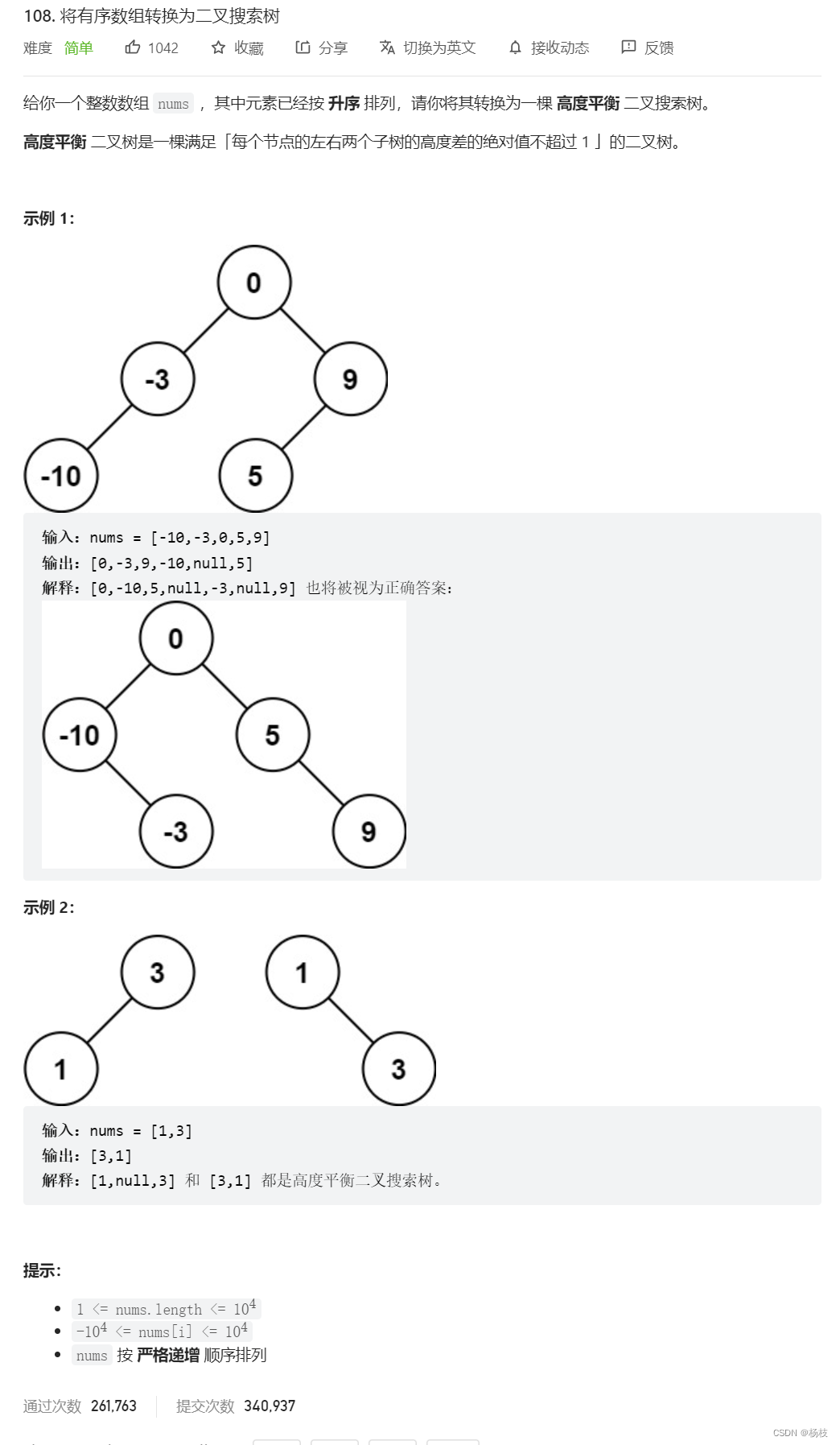
💓第五题 108. 将有序数组转换为二叉搜索树
递归 + 搜索二叉树的性质💒题目描述
🌟解题报告
递归的落实,自顶向下的搜索操作的结点,自底向上的将按照咱给定逻辑执行的若干个子解答回溯了汇聚起来,最后分别汇聚为暂定的根节点
root_node的左边的左子树的全部解以及右边的右子树的全部解。🌻参考代码(C++版本)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* dfs(vector<int> &nums,int l ,int r)
{
//持续找中点值,中点的左边是左子树,右边是右子树
if(l > r) return nullptr;
int mid = (l+r) >> 1;
//将中点处理为一个结点
TreeNode* root_node = new TreeNode(nums[mid]);
//中点左边的数据归结为左子树的内容,递归进去按照类似的逻辑处理
root_node->left = dfs(nums,l,mid-1);
root_node->right = dfs(nums,mid+1,r);
return root_node;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
int n = nums.size();
int l = 0,r = n - 1;
return dfs(nums,l,r);
}
};

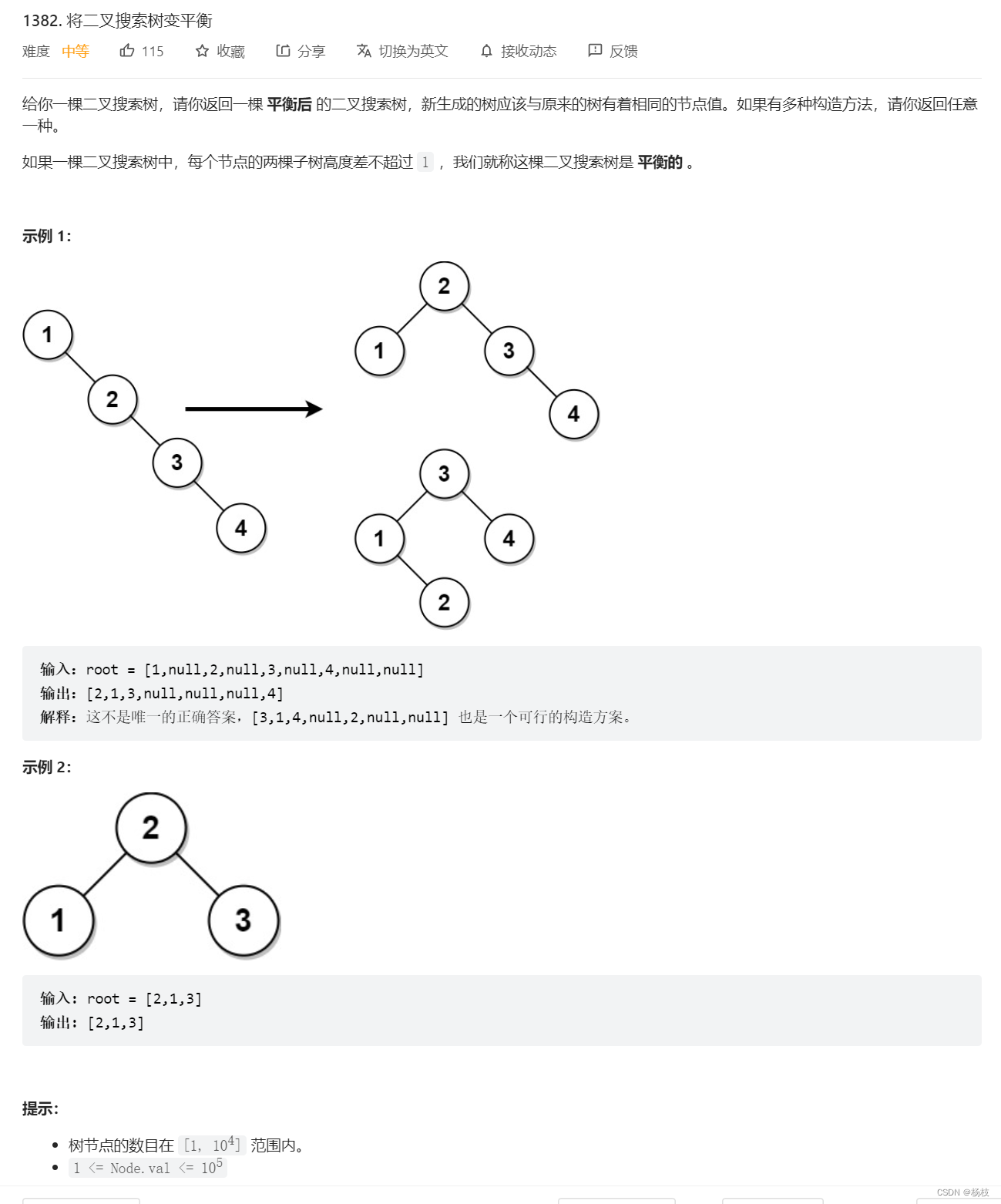
💓第六题 1382. 将二叉搜索树变平衡
💒题目描述
🌟解题报告
上一个题的变型,需要自己提前将树按照可以体现搜索二叉树形式的中序比那里存储到数组中,再按照上一题中,类似的方式,将数组存储的搜索二叉树按照你性质进行平衡
🌻参考代码(C++版本)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> tmp;
TreeNode* dfs(vector<int> &nums,int l,int r)
{
if(l > r) return nullptr;
int mid = (l + r) >> 1;
TreeNode* node = new TreeNode(nums[mid]);
//递归去加载平衡二叉树的左子树和右子树
//比当前中点小的是左子树,比当前中点大的是右子树
node->left = dfs(nums,l,mid-1);
node->right = dfs(nums,mid+1,r);
return node;
}
void to_arr(TreeNode *node)
{
if(!node) return;
to_arr(node->left);
tmp.push_back(node->val);
to_arr(node->right);
}
TreeNode* balanceBST(TreeNode* root) {
//先把当前的树的信息存放到数组中
tmp.clear();
TreeNode* m = root;
to_arr(m);
//现在就是和上一题一样的操作了
int n = tmp.size();
int l = 0 , r = n-1;
return dfs(tmp,l,r);
}
};

💓 总结
① 递归不要想太多,清楚当前这步,或者说当前这层函数想干嘛,具体想当前,再结合大局观去看这个递归的执行,就很好明白自顶向下的递归,和自底向上的回溯。
② 知道什么是搜索二叉树,搜索二叉树的特征是什么:
左子树的所有结点数值都小于根结点的数值
右子树的所有结点数值都大于根节点的数值
③ 搜索二叉树和中序遍历几乎是配合一起用的
二叉搜索树(BST)的中序遍历是升序
④ 树的递归,大多数要结合前序、中序、后序一起走