[数据结构与算法] 数据结构—

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 数据结构——图论 -> 正文阅读

[数据结构与算法]数据结构——图论

文章目录

https://vjudge.net/contest/492558

图论入门计蒜客 - T1325

问题描述

假设用一个 n×n 的数组 a 来描述一个有向图的邻接矩阵：

（1）编写一个函数确定一个顶点的出度
（2）编写一个函数确定一个顶点的入度
（3）编写一个函数确定图中边的数目

输入格式

第一行：节点总数 n、指定节点 m；下面 n 行：有向图的邻接矩阵

输出格式

第一行包括三个数据：节点编号 m、m 的出度、m的入度（之间用一个空格隔开）。
第二行包括一个数据：图中边的总数。

数据范围：1≤n, m, a[i][j]≤1000。

输入样例：

输出样例：

3 2 3
15

参考程序

#include<iostream>
using namespace std;
const int N=1e3+10;
int a[N][N];
int n,m; 
int in_degree(int j){
    int ans=0;
    for(int i=1; i<=n; i++){
        if(a[i][j]!=0) ans++;
    }
    return ans;
}
int out_degree(int i){
    int ans=0;
    for(int j=1; j<=n; j++){
        if(a[i][j]!=0) ans++;
    }
    return ans;
}
int number_sides(){
    int ans=0;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            if(a[i][j]!=0) ans++;
        }
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            cin>>a[i][j]; 
        }
    }
    cout<<m<<" "<<out_degree(m)<<" "<<in_degree(m)<<endl<<number_sides()<<endl;
    return 0;
}

p节点计蒜客 - T1421

问题描述

给出一颗有根树，总共 n 个节点，
如果一个节点的度不小于它所有的儿子以及他的父亲的度（如果存在父亲或者儿子），
那么我们称这个点为 p 节点，现在给你一棵树你需要统计出 p 节点的个数。

这里的度数指树上的度数，即一个节点的子节点数。

输入格式

输入的第一行包含一个整数 t（1≤t≤100），表示数据组数。
接下来 t 组数据，每组数据第一行一个数 n（1≤n≤1000），表示树的节点数。
然后 n-1 行，每行两个数 x，y（0<x,y<n），代表 y 是 x 的儿子节点。

输出格式

输出 t 行，每一行一个整数，代表 p 节点的个数。

输入样例

输出样例：1

参考程序

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
const int N=1e5+10;
int f[N]; // f[i] 表示 i的父节点 
vector<int> G[N];
int main(){
    ios::sync_with_stdio(false);
    int t; cin>>t;
    while(t--){
        memset(f, 0, sizeof(f));//多组数据，要初始化
        for(int i=1; i<N; i++) G[i].clear();
        int n,x,y; cin>>n;
        for(int i=1; i<n; i++){
            cin>>x>>y;
            G[x].push_back(y);
            f[y] = x; 
        }
        int ans=0;
        for(int i=1; i<=n; i++){
            bool flag=1;
            if(G[i].size()<G[f[i]].size()) continue;
            for(int j=0; j<G[i].size(); j++){
                if(G[i].size()<G[G[i][j]].size()){
                    flag = 0;
                }
            }
            if(flag) ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

A Knight’s Journey POJ - 2488

问题描述

整天待在一个方块里, 骑士感到特别的无聊, 于是, 他决定来一场所走就走的旅行
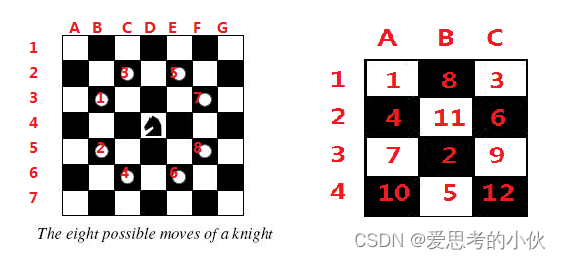
但他只能走日字, 并且世界是一个不大于 8*8 的棋盘.你能帮勇敢的骑士制定一个旅行计划吗?
请找出一条路使得骑士能够走遍整个棋盘.骑士可以在任一方块出发或结束。

输入格式

第一行输入一个正整数n, 代表数据组数
对于每组数据, 含有两个正整数 p 和 q (1 <= p*q <= 26), 表示一个 p*q 的棋盘.
每个方块的位置用两个字符表示, 第一个从A开始,代表列, 第二个从1开始,代表行。

输出格式

每组数据的结果首先是一行"Scenario #i:“, i是数据序号, 从1开始
然后输出一行, 是字典序第一的可以走遍棋盘的路径, 接着有一个空行
路径应该是连续的依次所走方块的位置
如果不存在这样的路径, 输出"impossible”

输入样例

输出样例：

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

在这里插入图片描述

参考程序

#include<iostream>
#include<string>
#include<cstring>
#include<cstdio>
using namespace std;
const int N=110;
int n,m,dis[][2]= {-1,-2, 1,-2, -2,-1, 2,-1, -2,1, 2,1, -1,2, 1,2};
int vis[N][N], s[N][2], flag=0;
void dfs(int x,int y,int step) {
   s[step][0]=x, s[step][1]=y, vis[x][y]=1;
   if(step==n*m) {
      flag=1; return;
   }
   for(int i=0; i<8; i++) {
      int tx = x+dis[i][0];
      int ty = y+dis[i][1];
      if(flag||vis[tx][ty]||tx<1||tx>n||ty<1||ty>m) continue;
      vis[tx][ty]=1;
      dfs(tx, ty, step+1);
      vis[tx][ty]=0;
   }
}
int main() {
//   freopen("data.in", "r", stdin);
   int t; scanf("%d", &t);
   for(int i=1; i<=t; i++) {
      scanf("%d%d",&n,&m);
      memset(vis, 0, sizeof(vis));
      flag=0;
      dfs(1,1,1);
      printf("Scenario #%d:\n",i);
      if(flag) {
         for(int i=1; i<=n*m; i++) {
            printf("%c%d",s[i][1]-1+'A',s[i][0]);
         }
      } else printf("impossible");
      printf("%s", i==t ? "\n":"\n\n");
   }
   return 0;
}

Avoid The Lakes POJ - 3620

问题描述
农夫约翰的农场在最近的一场风暴中被洪水淹没，而他的奶牛极度怕水的消息更是加剧了这一事实。
然而，他的保险公司只会根据他农场上最大的“湖”的大小来偿还他。

农场表示为一个包含 N 行和 M 列的矩形栅格。网格中的每个单元格要么是干燥的，要么是浸没的，其中K个单元格被浸没。正如人们所料，湖泊有一个中央细胞，其他细胞通过共享一条长边（而不是一个角）与之相连。任何与中央单元共享长边或与任何连接单元共享长边的单元都将成为连接单元，并且是湖泊的一部分。

输入格式
第1行：三个空格分隔的整数：N、M和K（1≤ N，M≤ 100，1≤ K≤ N×M）
第2…K+1行：第i+1行用两个空格分隔的整数描述了一个浸没位置，这两个整数是其行和列：R和C

输出格式
第1行：最大湖泊包含的单元数。

输入样例

输出样例：4

参考程序

#include<iostream> 
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e4+10;
int n,m,k,a,b,dis[][2]= {-1,0, 0,-1, 1,0, 0,1};
int ans=0,cnt=0,s[N][N];

void dfs(int x,int y){
    s[x][y]=0, cnt++;
    for(int i=0; i<4; i++){
        int tx=x+dis[i][0];
        int ty=y+dis[i][1];
        if(!s[tx][ty]||tx<1||tx>n||ty<1||ty>m) continue;
        dfs(tx,ty);
    }
}
int main(){
//    freopen("data.in", "r", stdin);
    scanf("%d%d%d", &n,&m,&k);
    for(int i=1; i<=k; i++) {
        scanf("%d%d",&a,&b); s[a][b]=1; 
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            if(s[i][j]==1){
                cnt=0;  dfs(i,j);
                ans=max(ans,cnt);
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

Dungeon Master POJ - 2251

问题描述

你进入了一个3D的宝藏地宫中探寻宝藏到了宝藏，
你可以找到走出地宫的路带出宝藏，或者使用炉石空手回家。
地宫由立方体单位构成，立方体中不定会充满岩石。
向上下前后左右移动一个单位需要一分钟。
你不能对角线移动并且地宫四周坚石环绕。
请问你是否可以走出地宫带出宝藏？如果存在，则需要多少时间？

输入格式

每个地宫描述的第一行为L，R和C（皆不超过30）。
L表示地宫的层数，R和C分别表示每层地宫的行与列的大小。
随后L层地宫，每层R行，每行C个字符。每个字符表示地宫的一个单元。
‘#‘表示岩石单元，’.‘表示空白单元。你的起始位置在’S’，出口为’E’。
每层地宫后都有一个空行。L，R和C均为0时输入结束。

输出格式

每个地宫对应一行输出。
如果可以带出宝藏，则输出 Escaped in x minute(s). x为最短脱离时间。
如果无法带出，则输出 Trapped!

输入样例

3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

参考程序

#include<iostream>// TLE
#include<cstdio>
#include<queue>
using namespace std;
const int N=110;
int dis[][3]= {0,0,1, 0,0,-1, 0,1,0, 0,-1,0, 1,0,0, -1,0,0};
int l,r,c,sx,sy,sz,ex,ey,ez;
char s[N][N][N]; 
struct T {
    int x,y,z,step;
    T() {}
    T(int a,int b,int c,int d) {
        z=a, x=b, y=c, step=d;
    }
};
int bfs() {
    queue<T> que; que.push(T(sz,sx,sy,0));
    while(!que.empty()) {
        T temp = que.front(); que.pop();
        s[temp.z][temp.x][temp.y]='#';
        for(int i=0; i<6; i++) {
            int tx = temp.x+dis[i][0];
            int ty = temp.y+dis[i][1];
            int tz = temp.z+dis[i][2];
            if(tx<0||tx>=r||ty<0||ty>=c||tz<0||tz>=l) continue;
            if(s[tz][tx][ty]=='E') return temp.step+1;
            if(s[tz][tx][ty]!='#') que.push(T(tz,tx,ty,temp.step+1));
        }
    }
    return -1;
}
int main() {
//    freopen("data.in", "r", stdin);
    while(~scanf("%d%d%d\n",&l,&r,&c)) {
        if(l==0&&r==0&&c==0) break;
        for(int i=0; i<l; i++) {
            for(int j=0; j<r; j++) scanf("%s\n",s[i][j]);
            for(int j=0; j<r; j++) {
                for(int k=0; k<c; k++) {
                    if(s[i][j][k]=='S') {
                        sz=i, sx=j, sy=k; break;
                    }
                }
            }
        }
        int ans=bfs();
        if(ans!=-1) printf("Escaped in %d minute(s).\n", ans);
        else printf("Trapped!\n");
    }
    return 0;
}