1. 5.最长回文子串
1.题目描述

2.题目解析
回文子串是指正着读反着读都一样的子串,所以可以
- 将字符串反过来,然后再比对两个字符串的最长相同长度即可;
- 中心扩散法:对每一位置,以该点为中心往两边扩散:首先分别往左右单边扩散,找到与中心点相同的字符,然后同时往两边扩散,得到两端点相同字符,最后记录最长的结果即为所求;
- 动态规划:
中心扩散:
其实可以进行优化,把记录max的右端点的变量去除,因为可以用长度和左端计算出来。一定注意每次循环都要把长度设置为1。
class Solution {
public String longestPalindrome(String s) {
if(s.length()==0||s.equals(""))return "";
int ss=s.length();
int ml=0;
int mr=0;
int max=0;
int len=1;
for(int mid=0;mid<ss;mid++){
int left=mid-1;
int right=mid+1;
while(left>=0&&s.charAt(mid)==s.charAt(left)){
left--;
len++;
}
while(right<ss&&s.charAt(right)==s.charAt(mid)){
right++;
len++;
}
while(left>=0&&right<ss&&s.charAt(left)==s.charAt(right)){
left--;
right++;
len=len+2;
}
if(max<len){
max=len;
ml=left+1;
mr=right-1;
}
len=1;
}
return s.substring(ml,mr+1);
}
}
动态规划:
使用boolean dp[i][j] 判断s的i到j子串是否为回文子串;
初始状态:dp[i][i]为true;
当s[i]==s[j]时,如果距离小于等于2或者dp[i+1][j-1]为true则该位置为true;
循环:从第二个字符开始,以每个字符为终点,然后再以该字符之前的每个字符为起点,进行判断。
class Solution {
public String longestPalindrome(String s) {
if(s==null||s.length()<2){
return s;
}
int ss=s.length();
int max=1;
int maxl=0;
int maxr=0;
boolean dp[][]=new boolean [ss][ss];
for(int r=1;r<ss;r++){
for(int l=0;l<r;l++){
if(s.charAt(r)==s.charAt(l)&&((r-l)<=2||dp[l+1][r-1])){
dp[l][r]=true;
if(max<r-l+1){
max=r-l+1;
maxl=l;
maxr=r;
}
}
}
}
return s.substring(maxl,maxr+1);
}
}
2. 6.Z字形变换
1.题目描述
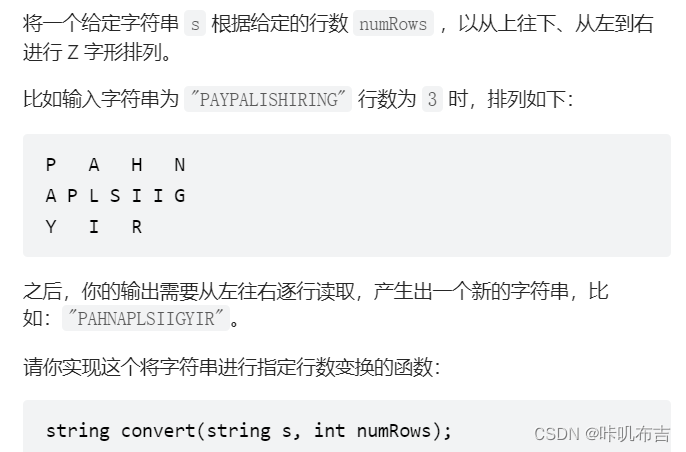
2. 题目解析
这道题不在热题100中,但是写都写了,接着写完吧。
z字变换其实就是先在第一行放一个字符,再在第二行,直至第numRows行,然后倒回去。所以可以用numRows个字符数组,来回存放其中即可。
class Solution {
public String convert(String s, int numRows) {
if(numRows < 2) return s;
List<StringBuilder> rows = new LinkedList<StringBuilder>();
for(int i = 0; i < numRows; i++) rows.add(new StringBuilder());
int i = 0, flag = -1;
for(int j=0;j<s.length();j++) {
rows.get(i).append(s.charAt(j));
if(i == 0 || i == numRows -1) flag = - flag;
i += flag;
}
StringBuilder res = new StringBuilder();
for(StringBuilder row : rows) res.append(row);
return res.toString();
}
}
3. 10.正则表达式匹配
1.题目描述

2.题目解析
先想人进行匹配的时候,先看p,再看s,一个字符一个字符地进行匹配,如果p是字母,则s必须有字母与之对应,如果p是. 则可以直接去除一个s字符,因为它永远适配,如果p是*,则可以匹配0次(s中一个不去掉)或者匹配无数次()。
空间存储:使用f[i][j]表示s的前i个与p的前j个字符是否匹配;boolean 数组的默认值为false
初始状态:f[0][0]为true;
转移方程:
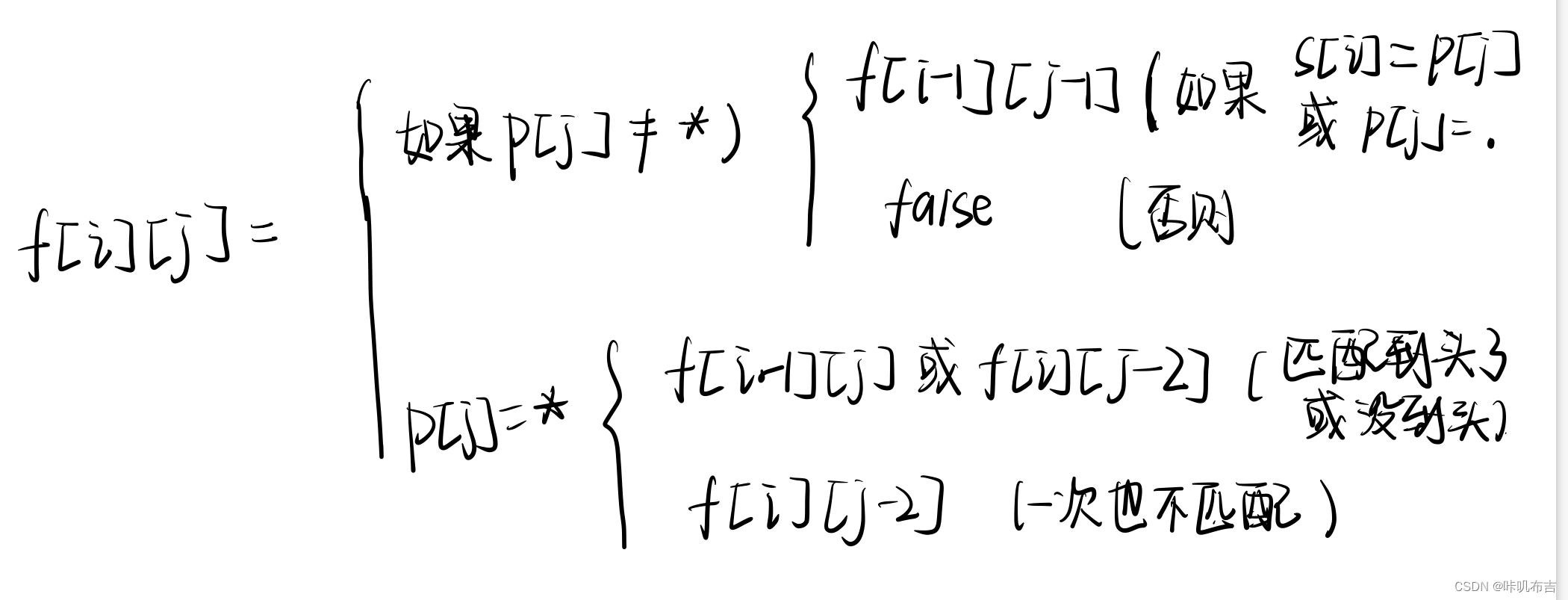
f[0][0]=true;其他i=0的f[0][j]=false,因为默认值为false,所以不用再次赋值;
然后在0-m与1-n的范围内进行遍历,分两种情况:p[j-1]是否为*(其实就是第j个字符);
如果为*,则f[i][j]=f[i][j-2],如果p的第j-1个字符与s的第i个匹配,则可以为f[i-1][j]或f[i][j-2];
如果不为*,则看s的第i个字符与p的第j个字符是否匹配。
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (i!=0&&(p.charAt(j-2)=='.'||p.charAt(j-2)==s.charAt(i-1))) {
f[i][j] = f[i][j-2] || f[i - 1][j];
}
} else {
if (i!=0&&(p.charAt(j-1)=='.'||p.charAt(j-1)==s.charAt(i-1))) {
f[i][j] = f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
}
4. 11.盛最多水的容器
1.题目描述

2. 题目解析
思路是题解中获取的,我用自己的语言梳理了一下:
这个问题是数组中找两个值,求其中较小的值与距离的最大乘积。
但是如何求呢,首先距离最大就是数组大小了,值最大就是数组中的最大值,但肯定取不到;
我们从两端开始,距离一直在缩减,那值呢?但看这两个小的值往里缩,可能最后的面积会增加或者减小,大的值往里缩会减小,所以每一次往里缩缩小值。
class Solution {
public int maxArea(int[] height) {
int j=height.length-1;
int i=0;
int res=0;
while(i<j){
if(height[i]<height[j]){
//i是小值,缩i,
res=Math.max(res,(j-i)*height[i++]);
}
else{
res=Math.max(res,(j-i)*height[j--]);
}
}
return res;
}
}
