AVL树是一种自平衡二叉搜索树。
在AVL树中,任何节点的两个子树的高度最多相差 1 个。
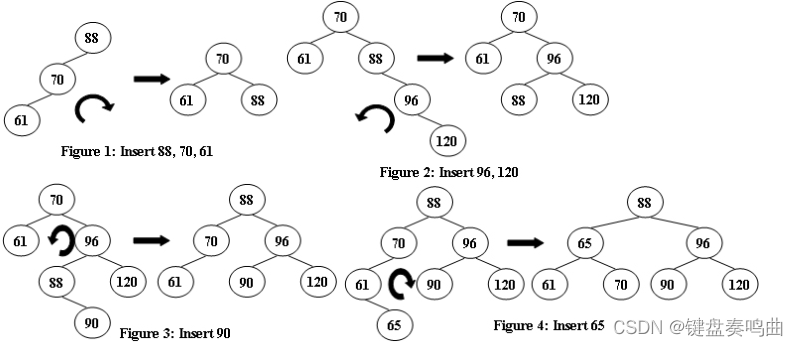
如果某个时间,某节点的两个子树之间的高度差超过 1,则将通过树旋转进行重新平衡以恢复此属性。
图 1?4 说明了旋转规则。
?
现在,给定插入序列,请你输出得到的AVL树的层序遍历,并判断它是否是完全二叉树。
输入格式
第一行包含整数 N,表示插入序列中元素个数。第二行包含 N 个不同的整数表示插入序列。
输出格式
第一行输出得到的AVL树的层序遍历序列。第二行,如果该AVL树是完全二叉树,则输出 YES,否则输出 NO。
数据范围
1≤N≤20
输入样例1:
5
88 70 61 63 65
输出样例1:
70 63 88 61 65
YES
输入样例2:
8
88 70 61 96 120 90 65 68
输出样例2:
88 65 96 61 70 90 120 68
NO
我的解法:
#include <bits/stdc++.h>
using namespace std;
const int N = 30;
int l[N], r[N], h[N], idx;
int v[N], q[N], pos[N];
int n;
int get_balance(int u){
return h[l[u]] - h[r[u]];
}
void update(int u){
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
void R(int &u){
int p = l[u];
l[u] = r[p];
r[p] = u;
update(u);
update(p);
u = p;
}
void L(int &u){
int p = r[u];
r[u] = l[p];
l[p] = u;
update(u);
update(p);
u = p;
}
void insert(int &u, int w){
if(!u){
u = ++idx;
v[u] = w;
}
else if(w <= v[u]){
insert(l[u], w);
if(get_balance(u) == 2){
if(get_balance(l[u]) == 1){
R(u);
}
else{
L(l[u]), R(u);
}
}
}
else{
insert(r[u], w);
if(get_balance(u) == -2){
if(get_balance(r[u]) == -1){
L(u);
}
else{
R(r[u]), L(u);
}
}
}
update(u);
}
bool bfs(int root){
q[0] = root;
pos[root] = 1; // 对应到完全二叉树中的1节点,pos用来判断是否是完全二叉树,我们可以先假设它是
bool res = true;
int hh = 0, tt = 0;
while(hh <= tt){
int t = q[hh ++]; // 出队
if(pos[t] > n) res = false;
if(l[t]) q[++tt] = l[t], pos[l[t]] = 2*pos[t]; // 出队
if(r[t]) q[++tt] = r[t], pos[r[t]] = 2*pos[t] + 1; // 出队
}
return res;
}
int main(){
cin >> n;
int root = 0;
for(int i = 0; i < n; i ++ ){
int w;
cin >> w;
insert(root, w);
}
bool res = bfs(root);
for(int i = 0; i < n; i ++ ){
cout << v[q[i]] << " ";
}
puts("");
if(res) puts("YES");
else puts("NO");
return 0;
}收获:
avl的操作看似复杂,其实很好背,熟练记忆后考场上直接默写
判断一棵树是不是完全二叉树,可以先假设这是一颗完全二叉树,然后层序遍历该二叉树,在遍历的过程中,引入pos[]来记录每个节点的位置,根据pos[ l[ t ] ] = pos[ t ]*2,pos[ r[ t ] ] = pos[ t ] * 2 + 1的性质给pos赋值,如果出现比n(节点数)要大的pos值,则证明假设不成立,该树不是一颗完全二叉树