题目

几乎每一个人都用乘法表。但是你能在乘法表中快速找到第k小的数字吗？

给定高度m 、宽度n 的一张 m * n的乘法表，以及正整数k，你需要返回表中第k 小的数字。

官方样例

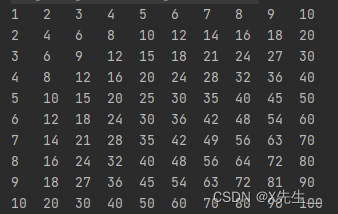
在这里插入图片描述

自测样例

在这里插入图片描述

题解思路（自测样例为数据）

将第k小的数字转化为有多少个数不超过 x 的个数
那么 x 的取值范围：[1,m*n] 即:[1,100]
为了加快速度，可以采用二分查找，取得 x 的值
我们通过发现，每一行的数据，其实都是 m 的倍数，最大的倍数 n 倍
那么，第一次 x = 50
1. 遍历第一行，50是1的50倍，最大的倍数 10 倍，即：个数为：10
2. 遍历第二行，50是2的25倍，最大的倍数 10 倍，即：个数为：10
3. 。。。
4. 遍历第六行，50是6的8倍，最大的倍数10倍，即：个数为：8
5. 。。。
综上所诉，通项公式即是： $\sum_{i=1}^{m} min(x / i,n)$
如果还要精益求精，则可以将通项公式化简
1. 如果 x / i ≥ n ，则 x 大于 n * i，个数为：x/n * n (PS:一定要进行取整)
2. 如果 x / i < n ，则 x 小于 n * i，个数为：x / i
3. 可能这个时候，有的人要问了，x / i = n 为什么不能直接返回 x ，那是因为：x 可能不在乘法表里面

AC代码·暴力版

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int left = 1;
        int right = m * n;

        while (left < right) {
            int x = (left + right) / 2;
            int count = 0;
            for (int i = 1; i <= m; i++) {
                count += Math.min(x / i,n);
            }
            if(count >= k){
                right = x;
            } else {
                left = x + 1;
            }
        }
        return left;
    }
}

AC代码·精益求精版

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int left = 1;
        int right = m * n;

        while (left < right) {
            int x = (left + right) / 2;
            int count = (x / n) * n;
            for (int i = x / n + 1; i <= m; i++) {
                count += x / i;
            }
            if(count >= k){
                right = x;
            } else {
                left = x + 1;
            }
        }
        return left;
    }
}