着色问题是很经典的一个问题,就是地图上的着色,首先有一个图用颜色着色,着色的要求就是任何的一条边,它的两个顶点是不能够才用同一个颜色的,要采用不同的颜色,图是无向的连通图(从一个顶点可以到达另外一个顶点,不存在过不去的情况),这里面的每一条边将两个顶点连起来,这个时候找所有的着色方案。
一、问题描述
输入:无向连通图G和m 种颜色的集合用这些颜色给图的顶点着色,每个顶点一种颜色. 要求是:G 的每条边的两个顶点着不同颜色.
输出:所有可能的着色方案。 如果不存在着色方案,回答“No”
二、实例
左边是有7个顶点的连通图,现在有三种颜色能将每个顶点涂上不同的颜色,第1个顶点涂成红色,第2个顶点涂成蓝色,……任何一条边两端的颜色都不一样,这就是一个着色方案。
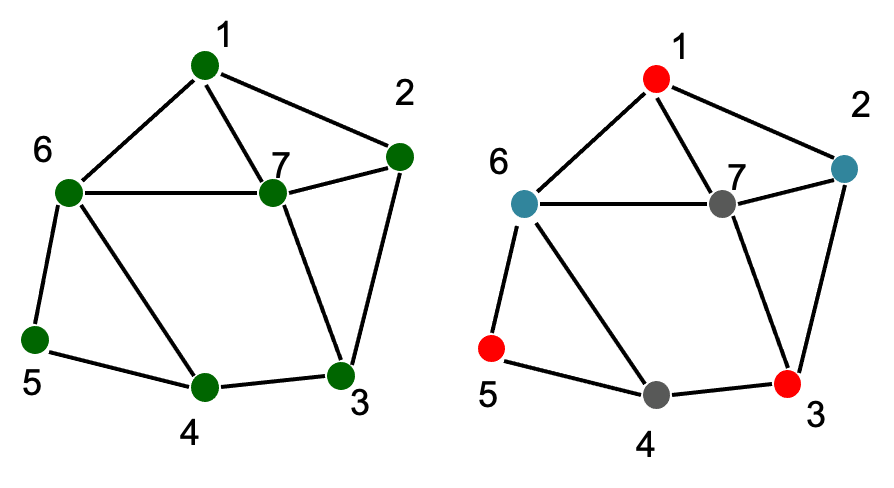
n=7, m=3
三、解向量
回溯算法第一步就是研究解,这个解其实是一个向量,因为每个顶点都要着色,所以它是一个跟顶点个数相同的一个向量。
设G=(V,E),V={1,2, … , n}
1、颜色编号:1, 2, … , m
2、解向量:
<
x
1
,
x
2
,
.
.
.
,
x
n
>
,
x
1
,
x
2
,
…
,
x
n
∈
1
,
2
,
.
.
,
m
<x1, x2, ..., xn>, x1, x2, …, xn∈{1,2, .., m }
<x1,x2,...,xn>,x1,x2,…,xn∈1,2,..,m
结点的部分向量
<
x
1
,
x
2
,
…
,
x
k
>
x
1
,
x
2
,
…
,
x
k
,
1
≤
k
≤
n
,
<x1, x2 , … , xk> x1, x2, …, xk, 1 ≤k ≤n,
<x1,x2,…,xk>x1,x2,…,xk,1≤k≤n,
表示只给顶点1,2,…,k着色的部分方案
四、算法设计
1、搜索树:m叉树
向量的每一个分量上赋一种颜色编号,颜色编号的可选集合在m中去选择,编号每个分量的范围是1…m,要求的向量的长度是n,最后要求得的是m叉树,每个顶点可能有m中选择,这个顶点着完色以后就对它的下一个顶点进行着色,下一个顶点着色的时候,有m-1种选择,这样继续遍历,直到找到一条路径能够到达叶结点。
也就是说,对所有的顶点都找到一个着色的方案,达到最后找到一个路径,每个路径的顶点都找到一个着色的方案,每个路径的上面都有编号,把这些编号连接起来就是着色方案。
2、约束条件
在结点<x1, x2, … , xk>处,顶点k+1 的邻接表中结点已用过的颜色不能再用
如果邻接表中结点已用过m种颜色,则结点k+1没法着色,从该结点回溯到其父结点, 满足多米诺性质
注:
在着色的时候需要记录这个点的邻接点,从上面往下遍历,一种可能:走到一个点和它相连的一些点很可能已经有颜色了(着过色了),着过色的这些点里面的颜色总数已经有m种了,那么对它而言没有办法再着色了

另外一种可能,前面和它相连的点已经有m-1种颜色,那这个点就只有一种选择。唯一的一种选择去放进去,再往下搜索观察和它相临的那些点的着色。

3、搜索策略
深度优先
4、时间复杂度
O ( n m n ) O(n m^n) O(nmn)
五、总结
在NP完全性角度,着色问题、装载问题是判定问题,0-1背包或者完全背包问题,装的总value达到最大越好,在活动的安排上,一个接一个,安排的最大的相容集,尽可能满足大部分人的需要,一些活动安排妥当,使得各个客户得到满足,一类问题是回答yes or no的问题,另外一类问题就是能不能找到最大的装入背包的物品的价值,能不能找到最大的安排的序列,满足最大的客户的需要,这是两种不同的回答,所有的优化问题是可以转化为判定问题的,
背包问题可以设定一系列的阈值,将阈值设定为100,有没有可能有一种装法让最终的总价值超过100,回答yes or no,超过了100有没有可能有一种装法让最终的总价值超过200,回答yes or no,超过了200有没有可能有一种装法让最终的总价值超过300,回答yes or no,…不停的设阈值,直到回答no,然后在把阈值向下减。最后只要回答yes or no,就能猜到心中的那个数,这种优化问题经过设置不同的阈值是可以装花城判定问题的。判定问题的输出只有0和1,回答yes or no。
研究单独的问题的时候,就像泛函中学的,从算法复杂性的角度来看,从问题角度哪些问题可以归为一类,然后再从更高层面来研究问题本身的属性,这就是NP的研究。
