1. 朴素模式匹配算法

（1）定义：
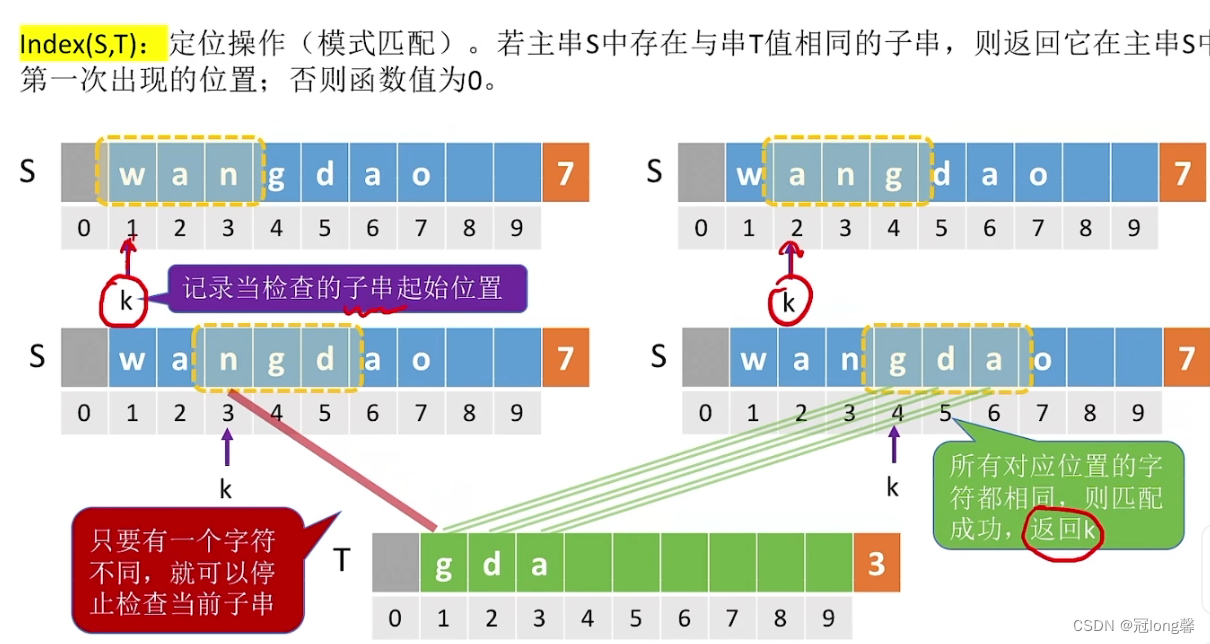
在主串中找到与模式串匹配的子串，并返回字串的位置。

思想：

从主串的第一位开始，逐个判断子串是否匹配模式串。
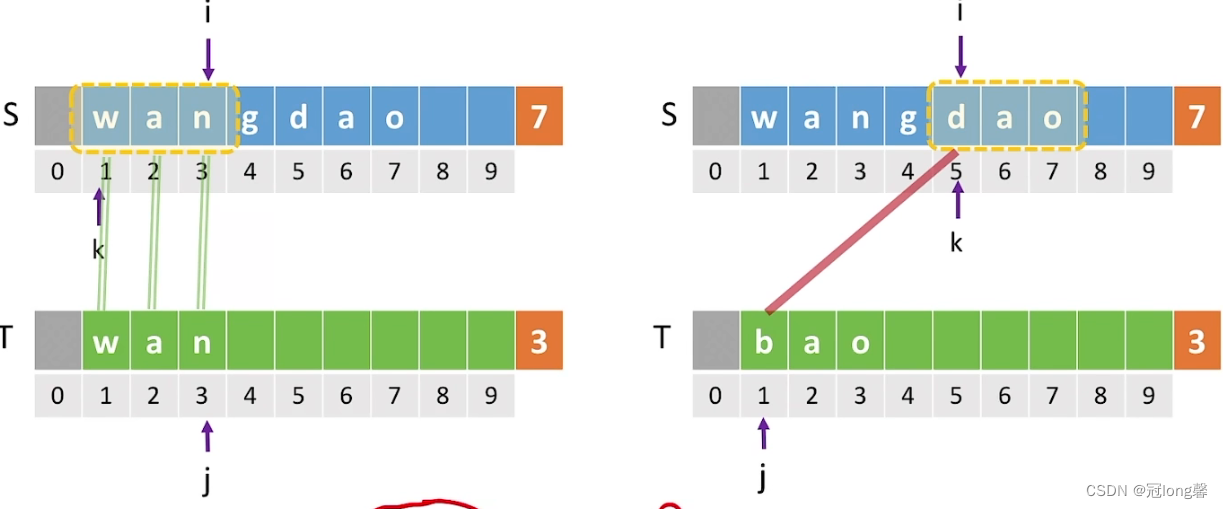
①当子串所有对应位置字符都和模式串相同时，查找成功，返回子串起始位置k。
②如果有一个字符不匹配，停止检查当前子串。

（2）代码
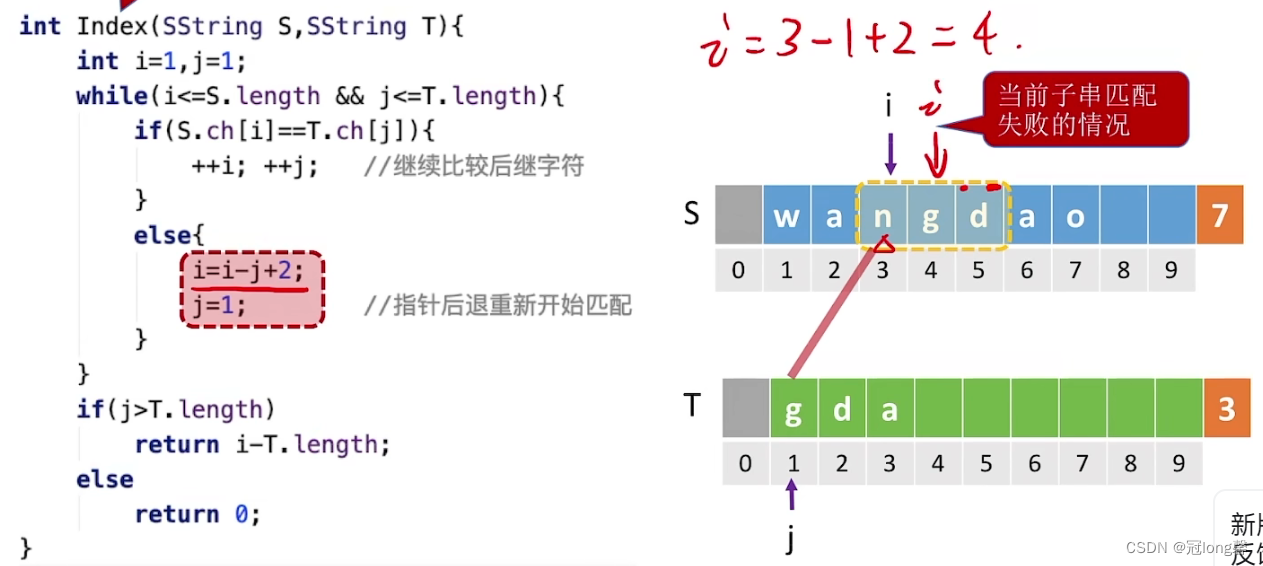
若当前子串查找失败，需要回溯到下一个子串开始的位置，因此可以令 $i = k + 1$ 或者 $i = i ? j + 1$ （子串起始位置以1为单位从左往右增大，此时字符串的起始位置是0）。当遍历完整个主串仍未获得匹配子串时，匹配失败。

int Index(string S, string T) {
	int i =0, j =0, k =0;
	while(i <S.size() && j <T.size()) {
		if(S[i] == T[j]) {
			i++;	
			j++;
		}
		else {
			k++;
			i = k;
			j = 1;
		}
	}
	if(j >=T.size())			// 查找成功
		return k;
	else return 0;
}

在这里插入图片描述

（3）性能分析
假设主串长为n，模式串长为m。主串中有n-m+1个候选匹配子串。

较好的情况：每个子串的第一个字符与模式串不匹配。
①匹配成功最好时间：O(m)
②匹配失败最好时间：O(n-m+1)=O(n)
匹配成功/失败最多需要：O((n-m+1)*m)=O(mn)

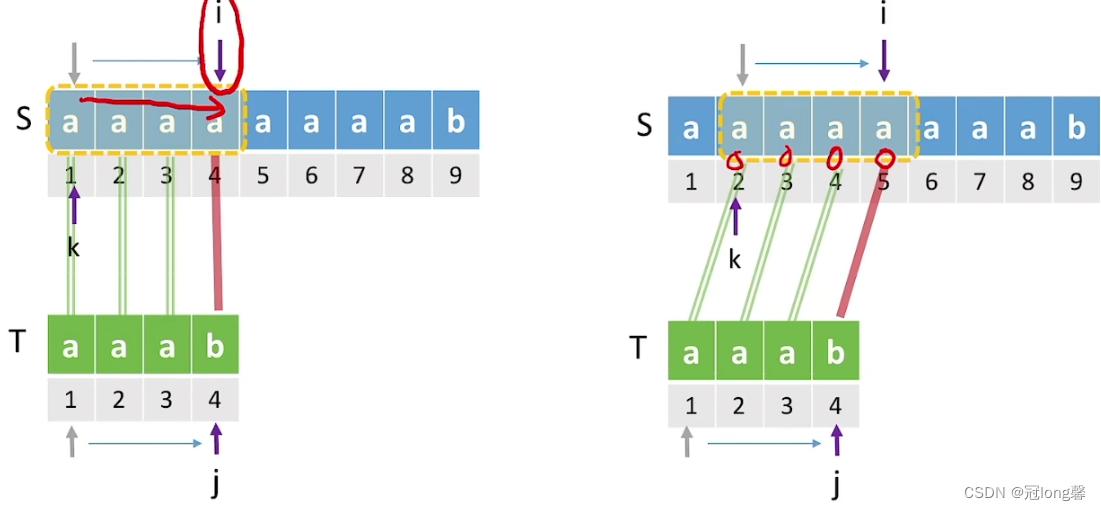
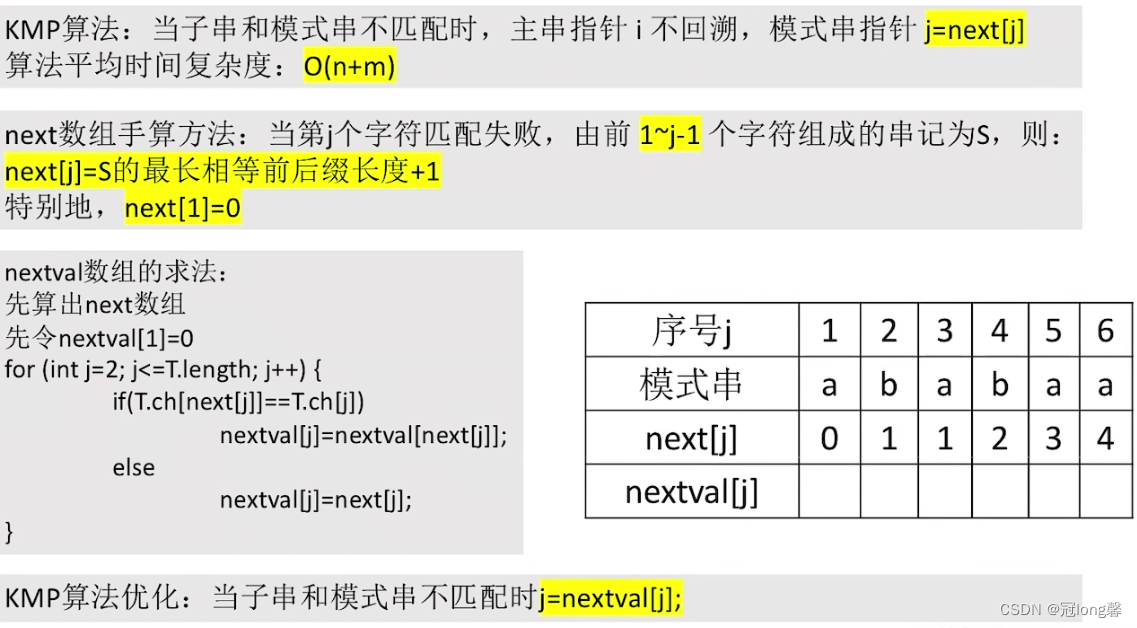
2. KMP算法

在朴素模式匹配算法中，子串匹配失败后模式串右移一位，主串指针回溯到下一个字符。这种回溯在存在部分匹配时是很低效的。如果第i个字符匹配失败，则前i-1个字符是匹配成功的。简单的向前回溯，会导致多次无用的查询。
考虑到人脑是具有记忆能力的，我们不会机械的每次仅从主串的下一个位置开始考虑。而是会从可能形成匹配的子串位置开始考虑。这样能够避免大量的回溯操作。那么机器如何实现这样的思想呢？
（1）思想

仅模式串指针需要回溯，主串不必回溯。
定义一个next数组，保存所在位置字符匹配失败后模式指针的指向变化。
①当j=-1时，表示主串中第i个字符与目标串首字符不匹配，主串指针后移一位。
②当 $s [i]! = t [j]$ 时，令 $j = n e x t [j]$ 使目标串右移到合适位置。

int Index_KMP(string s, string t, int next[]) {
	int i=0, j=0;
	while(i <s.size() && j <t.size()) {
	// 当j=-1时表示当前子串第一个字符与目标串不匹配。
		if(j==-1 || s[i] == t[j]) {
			i++;
			j++;
		}
		else
			j = next[j];		// 模式串向右移动
	}
	if(j >=t.size())
		return i;
	else 
		return 0;
}

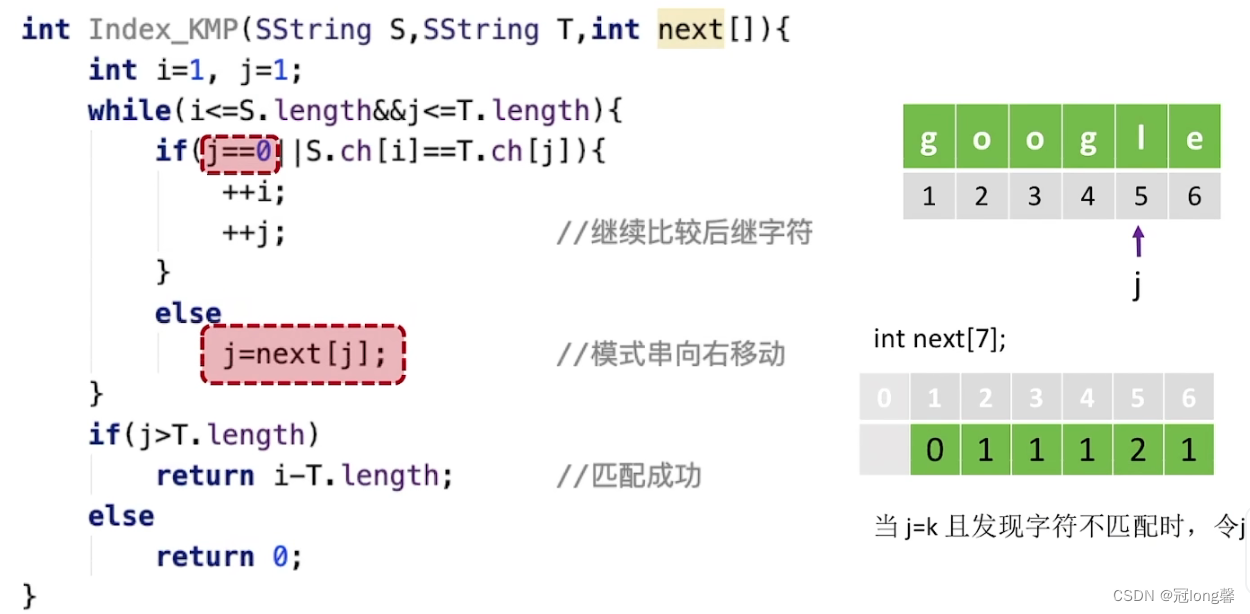
在这里插入图片描述
现在问题转换为了如何求next数组？这也是KMP算法的难点所在。

2.1 求模式串的next数组

在讲解如何求next数组前，我们先介绍几个概念：
优先选择上下匹配长度最大的位置

串的前缀：包含第一个字符，且不包含最后一个字符的子串。
串的后缀：包含最后一个字符，且不包含第一个字符的子串。
部分匹配值：当目标串的第j个字符匹配失败时，由1-j-1个字符组成串S，串S是当前子串的部分匹配值。

假设有部分匹配值‘ababab’，我们可以看出它有的最长相同前后缀为‘abab’。所以在下一次判断我们希望将目标串指针移植最长相同前后缀长度+1的位置，因为这是最早的可能匹配的位置。这种方法相对于朴素匹配算法能够减少无效匹配次数，同时也是对从不匹配位置从新开始匹配方法的修正（这样会丢失部分前缀信息，导致查找失败）。
因为next数组是根据相同前后缀获取的，因此可以直接通过目标串t获得。

（1）思想
假设i表示目标串的第i个字符（也可以理解为后缀末尾位置），j表示相同前缀末尾位置。整个算法是一个相同前后缀匹配的过程。

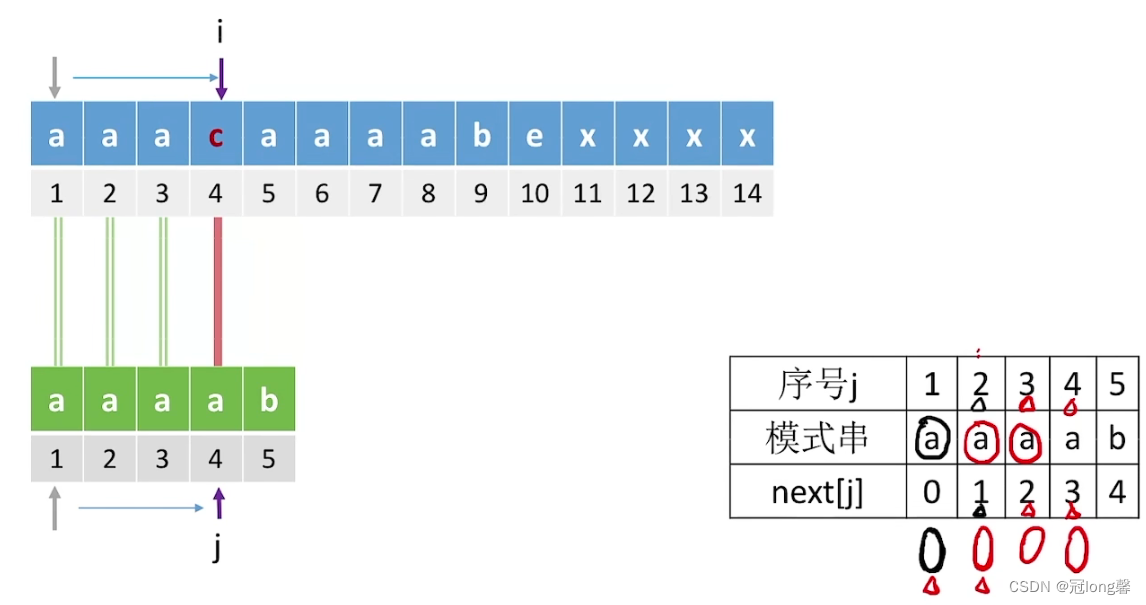
距离：求字符串’abababce’的next数组。
①i=0, j=-1时，获得i=1, j=0, next[1] = 0.因为字符b前最长相等前后缀长度为0，当字符b匹配失败后，目标指针会回到0位置，从a开始重新比较而无法利用过往的匹配信息。
②i=1, j=0时，获得j=next[0]=-1。接着i=2, j=0，获得next[2] = 0。因为字符a最长前后缀匹配长度为0，因此返回首位置a重新匹配。
③i=2, j=0时，获得i=3, j=1, next[3] = 1。因为b的最长相同前后缀长度为1’a’，所以字符b匹配失败后可以回到1位置开始匹配。
④…
⑤i=6, j=4时，因为’a!=c’获得j=next[4]=2。又因为’a!=c’获得j=next[2]=0。又因为’a!=c’获得j=next[0]=-1。因为j=-1，i=7,j=0,next[7]=0。表示对于字符e如果匹配失败因为相同前后缀长度为0，会从目标字符的首个元素开始判断。
通过上面的模拟我们可以得知：
算法通过i, j获得next[i+1]的值。i为后缀末位索引，j为前缀末位索引。当t[i]=t[j]时，对于字符i+1而言，表示在它的前面i个字符中，是有相同前后缀的。因此当i+1字符匹配失败后，可以从后缀的后一位移动到相等前缀的后一位，也就是j++。当j=-1时，表示了当前字符与目标首字符不相同，所以跳过当前字符i。

void get_next(string t, int next) {
	int i =0, j=-1;
	next[0] = -1;
	while(i < t.size()) {
		// 通过j~i确定第i+1个字符的next值 next[i+1]
		if(j==-1 || t[i] == t[j]) {
			i++;
			j++;
			next[i] = j;	
		}
		// 向前找匹配前后缀直到从首元素开始判断。
		else 
			j = next[j];
	}
}

（3）性能分析
平均时间复杂度：O(m+n)。

2.2 优化next数组

通过2.1中的实例分析我们可以发现如果在模式串中的i位置字符匹配失败，会跳转到next[i]进行比较。但是当 $t [n e x t [i]] = = t [i]$ 即跳转后字符与跳转前字符相等，则又会继续跳转，造成很多无效比较。因此我们希望将跳转前后的相同字符回到最早出现的位置。
在这里插入图片描述
（1）思想

获得next数组以后，从第二个字符开始遍历整个数组。如果 $t [j] = t [n e x t [j]]$ ，则令 $n e x t [j] = n e x t [n e x t [j]]$ 。这样就可以对相同字符的多次无效比较。

void get_nextval(string t, int next[], int nextval[]) {
	nextval[0] = -1;
	for(int j=1; j<t.size(); j++) {
		if(t[j] == t[next[j]])
			nextval[j] = nextval[next[j]];
		else 
			nextval[j] = next[j];
	}
}