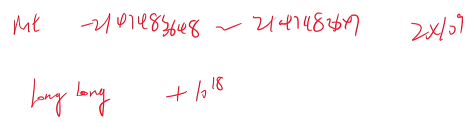如何判断一个算法能不能用?怎么判断一个算法的时间复杂度是否达标?
C++ 的评测姬 1 秒之内大概可以运行 1 亿次,就会达到上限,也就是 10^8 次,如果一个算法时间复杂度小于 10^7 或者 10^8 就是 ok 的,可以在 1 秒之内算出来,如果时间复杂度超过 10^8,就会导致超时
计算机中的 logn 一般指的是 log 以 2 为底的 n,数学上的 logn 一般指的是 log 以 10 为底的 n
如果题目的数据范围 n ≤ 30,可以使用指数级别的时间复杂度,暴搜、状态压缩 dp
如果题目的数据范围 n ≤ 10w,O( n^2 ) 就会超时 (10^5)^2 = 10^10 > 10^8,如果数据范围为 10w,时间复杂度要控制在 O( nlogn ) 或者 O( n )
如果题目的数据范围 n ≤ 10^7,基本上只能用 O( n ),10^7 × log2 10^7 = 2.3 × 10^8,log2 10^6 = 20
如果题目的数据范围 n ≤ 10^9,指的是 n 不超过 int 的范围,只能用 O( √ n ) 的时间复杂度
如果题目的数据范围 n ≤ 10^18,指的是 n 不超过 long long 的范围

不同变量的范围如下:
递归
写一个函数,在函数其中的某一个部分调用自己,例如求斐波那契数列:动态规划DP_小雪菜本菜的博客-CSDN博客

递归就是自己调用自己
输入一个 n,返回一个斐波那契数列:如果首项是 1,第二项是 2,从第三项开始每一项是前两项的和
//cin/cout
#include <iostream>
//scanf()/printf()
#include <cstdio>
//memset()
#include <cstring>
using namespace std;
int f(int n)
{
//两个边界
//第一种情况
if(n == 1) return 1;
//第二种情况
if(n == 2) return 2;
return f(n - 1) + f(n - 2);
}
int main()
{
int n;
//输入一个n
cin >> n;
//返回一个斐波那契数列
cout << f(n) << endl;
return 0;
}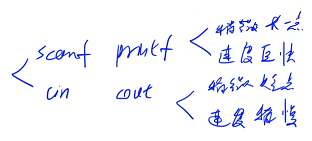
scanf 和 cin 的区别?
输入数的规模是小于 10^5,用 cin 和 scanf 时间上差不多;输入数的规模是大于等于 10^5,推荐使用 scanf,大概会快一倍左右
数据规模为 10^5,上面是 cin,下面是 scanf,所以读入数据规模比较大的时候,所以推荐使用 scanf

输出对比:上面是 printf,下面是 cout

递归的执行顺序
所有的递归都可以转换成一棵递归搜索树
下面想求 f( 6 ) 的递归搜索树
6 既不等于 1,也不等于 2,如果想求出 f( 6 ),必须要先求出 f( 5 ) 和 f( 4 )
c++ 在执行的时候,一定是一行一行来执行的,判断 n == 1,不成立,判断 n == 2,不成立,然后判断 return f( n - 1) + f( n - 2 ),在第 3 句代码中有可能从左到右算,有可能从右到左算,以从左到右算为例,会先执行 f( n - 1),先会递归到 f( n - 1) 里面去,算 f( 5 ),在 f( 5 ) 里面做判断,f( 5 ) 也既不是第一种情况( n != 1 ),也不是第二种情况( n != 2 ),因此继续把 f( 5 ) 分解成 f( 4 ) 和 f( 3 ). . .继续分解,在 f( 3 ) 里面继续分解,把 ( 3 ) 分解成 f( 2 ) 和 f( 1 ),f( 2 ):当 n = 2 的时候返回 2,因此 f( 2 ) 的值就是 2 ,f( 1 ):当 n = 1 的时候返回 1,f( 2 ) 和 f( 1 ) 执行完之后,相当于是 f( 3 ) 执行完了,返回的就是 f( 2 ) + f( 1 ) 的结果,因此 f( 3 ) = 3,因此 f( 3 ) 就执行完了,应该返回到 f( 4 ),在 f( 4 ) 里面已经算完第一项是 f( 3 ),会计算第二项 f( n - 2 ) 也就是 f( 2 ),f( 3 ) 和 f(2) 执行完之后,最终 f(4) 返回. . .
每个值都可以在边界的时候被算出来
任何一个递归的函数都可以对应这样一棵递归搜索树
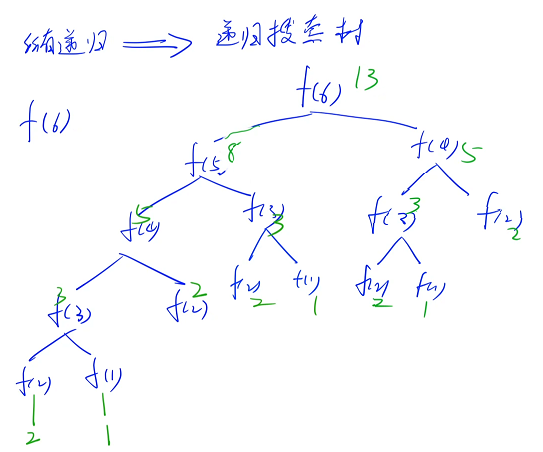
这个递归写法比较慢,最坏情况下每个点都可以分成两个分支,一共有 n 步,每一步分成两个分支,时间复杂度是 2^n 级别
递归搜索中的剪枝就是砍掉树的一个分支

下面的两道题涵盖了大部分递归的形式
递归实现指数型枚举
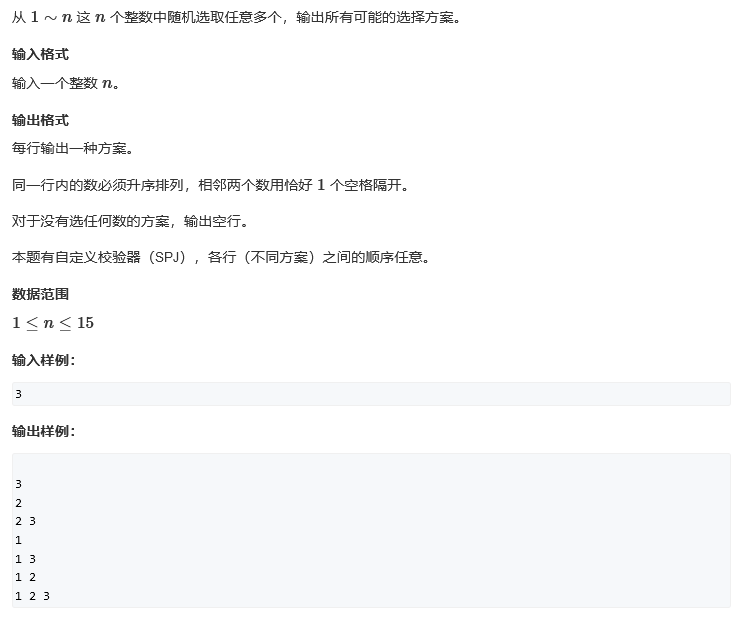
数据范围:n = 15,时间复杂度可以为 O( 2^n ) 或者 O( n × 2^n ),15 × 2^15 = 15 × 32768 = 15 × 3w = 45w
常见的 2^n 如下:
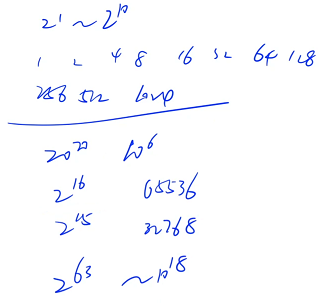
从 n 个数中随机选任意多个,然后输出所有可能的方案
1 ~ n 共有 n 个数,每个数有选和不选两种情况,总共的方案数就是 2^n
一共有 2^n 种情况,把所有的方案输出,每个方案长度是 n,时间复杂度就是 n × 2^n
答案不一定要按顺序输出,前后两行交换一下也是可以的
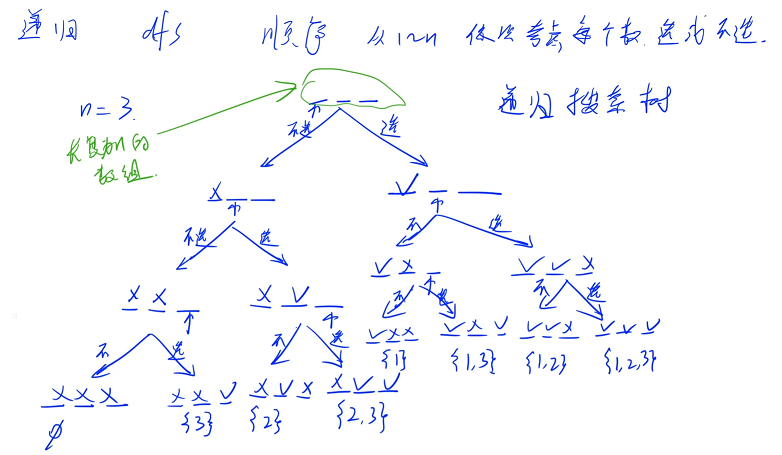
递归做法:最重要的是顺序,需要想一个顺序把不重复不漏地把所有的方案找出来
从前往后( 1 ~ n )依次考虑每一个数选或者不选,假设 n = 3 画出递归搜索树,一共有 8 种方案
一开始的时候,每一个数都没有考虑,需要从前往后考虑每一个位置,先考虑第一个位置,对于第一个位置来说有两种方案:选或不选,先递归第一个分支,再考虑第一个分支的第二个位置
注意空和不选和选是有区别的
下面考虑如何用代码来实现?
①需要记录递归搜索树的状态,当前每个位置是选、不选、还是没有考虑过,一共有 3 种状态,需要把它记录下来,因此可以开一个长度是 n 的数组来记录
当我们已经枚举完最后一个位置的时候,递归到下一层就已经在边界了,枚举完 u 之后,u 就会往后挪一位,边界的位置应该是 n
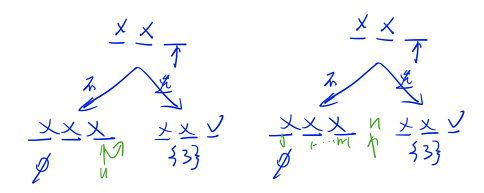
假设当前处在某个节点,在这个节点里面会分成两种情况来做,第一种情况是如果不选它的话,st[ u ] = 2,然后递归到下一个位置,如果不选它相当于把这个位置标成了 2,递归完之后(从这个位置搜完了),要往前回溯的话,应该把变之后的状态恢复成变之前的状态,(往左边分支搜索是初始状态,往右边分支搜索也应该是初始状态,对于所有儿子来说,都应该是公平的),因此我们需要恢复现场
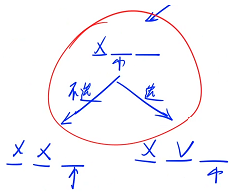
注意:递归一定要注意恢复现场,不管从当前点向哪个儿子走过去,都要保证当前的状态是一样的,不能让儿子去影响我的决策,所以需要恢复现场,怎么变过去的就要怎么变回来
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 16;
int n;
//定义一个数组记录每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它
int st[N];
//u表示当前在做第几位
void dfs(int u)
{
//判断边界:当n等于多少的时候是边界呢?
if(u > n)
{
//在返回之前,需要先把这个方案输出,这个方案是什么呢?
//从前往后遍历每一位,看一下这一位有没有选
for(int i = 1;i <= n;i++)
//如果当前位置是1的话,表示选了它就把他输出否则不输出
if(st[i] == 1)
printf("%d ",i);
printf("\n");
//到边界位置不能继续递归,需要返回
return;
}
//分支的过程
st[u] = 2; //第一个分支:不选
dfs(u + 1); //递归到下一个位置
st[u] = 0; //恢复现场
st[u] = 1; //第二个分支:选
dfs(u + 1); //递归到下一个位置
st[u] = 0; //恢复现场
}
int main()
{
//读入n
cin >> n;
//当前枚举到第几位,从1开始,枚举到第n位
dfs(1);
return 0;
}如果想把方案记录下来而不是中间输出的话,可以先把它存储下来
需要记录每个方案的个数,每个方案的个数并不一定是 n,(不一定把所有数都选掉,可以选任意多个数),需要记录每个方案的个数
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 16;
int n;
//定义一个数组来表示每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它
int st[N];
//开一个二维数组记录所有方案 一共有2^15次方个方案 每一个方案有15个数,下标从1开始
int ways[1 << 15][16];
//表示当前方案的数量
int cnt;
void dfs(int u)
{
//判断边界:当n等于多少的时候是边界呢? 当n枚举完最后一个位置的时候
if(u > n)
{
//在返回之前,需要先把这个方案输出这个方案是什么呢?
//从前往后遍历每一位看一下这个方案有没有选
for(int i = 1;i <= n;i++)
if(st[i] == 1)
//如果当前位置是1的话
ways[cnt][i] = i;
//方案数加1
cnt ++ ;
//到边界位置不能继续递归,需要返回
return;
}
st[u] = 2;
dfs(u + 1); //第一个分支:不选
st[u] = 0; //恢复现场
st[u] = 1; /* 会覆盖st[u] = 0 */
dfs(u + 1); //第二个分支:选
st[u] = 0; //恢复现场
}
int main()
{
//读入n
cin >> n;
//当前枚举到第几位
dfs(1);
for(int i = 0;i < cnt;i++)
{
for(int j = 1;j <= n;j++)
{
//特判如果是0的话就不输出
if(ways[i][j] == 0)
continue;
printf("%d ",ways[i][j]);
}
puts("");
}
/* puts():输出一个字符串加上一个回车 字符串为空等价于只输出回车 */
return 0;
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 16;
int n;
//定义一个数组来表示每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它
int st[N];
//每个方案用vector存储
vector<vector<int>> ways;
void dfs(int u)
{
//判断边界:当n等于多少的时候是边界呢? 当n枚举完最后一个位置的时候
if(u > n)
{
//定义一个当前的方案
vector<int> way;
//在返回之前,需要先把这个方案输出这个方案是什么呢?
//从前往后遍历每一位看一下这个方案有没有选
for(int i = 1;i <= n;i++)
if(st[i] == 1)
//如果当前位置是1的话,在当前方案里面插入i
way.push_back(i);
ways.push_back(way);
//到边界位置不能继续递归,需要返回
return;
}
st[u] = 2;
dfs(u + 1); //第一个分支:不选
st[u] = 0; //恢复现场
st[u] = 1; /* 会覆盖st[u] = 0 */
dfs(u + 1); //第二个分支:选
st[u] = 0; //恢复现场
}
int main()
{
//读入n
cin >> n;
//当前枚举到第几位
dfs(1);
for(int i = 0;i < ways.size();i++)
{
for(int j = 0;j < ways[i].size();j++) printf("%d ",ways[i][j]);
puts("");
}
/* puts():输出一个字符串加上一个回车 字符串为空等价于只输出回车 */
return 0;
}vector 存储比直接输出慢两倍左右

递归实现排列型枚举?
数据范围:9
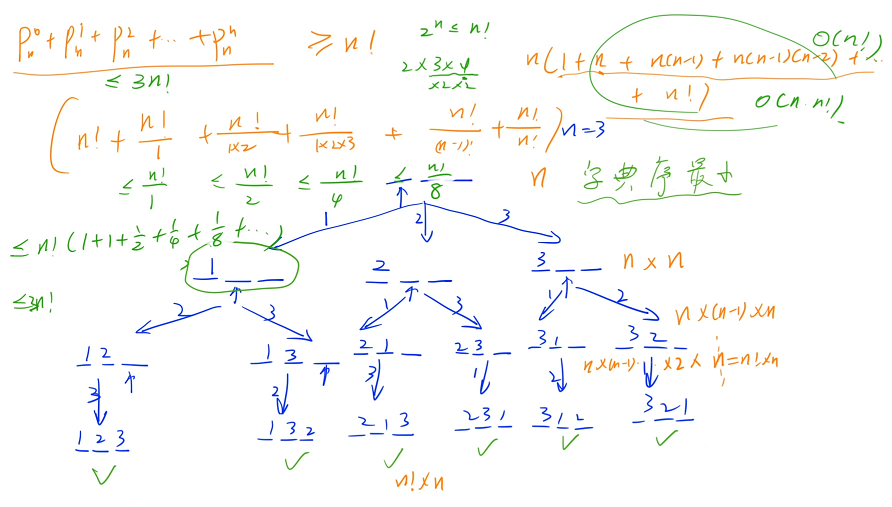
9! = 326880,时间复杂度为 n × n!,输入一个 n,输出 n 所有可能的排列,要按照字典序来输出
什么是字典序?
对于两个序列或者两个字符串来说,第一个字符串为:a1,a2,. . . an,第二个字符串为:b1,b2,. . . bn?
它们的字典序怎么比较呢?

先比较 a1 和 b1,如果相同的话,再比较 a2 和 b2,只要相同就一直往后比较,出现不同的情况:如果 ai < bi,说明序列 A? < 序列 B;如果 ai > bi,说明序列 A > 序列B;如果比较完最后一位,都发现 a 序列和 b 序列的每一个 i 都相等,就说明序列 A = 序列 B
如果 ai 不存在,但是 bi 存在,就认为 ai < bi
什么是全排列?
如果 n = 3,全排列有如下 6 种
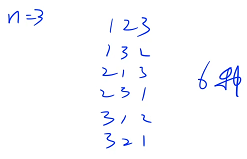
对于任意一个 n 来说,怎么把它的所有全排列输出出来呢?
可以用递归来做,需要先想一个顺序,可以不重不漏地把所有方案枚举出来
这道题目的顺序有很多种枚举方式
顺序 1:1、2、3 有 3 个数需要放在 3 个位置,先枚举 1 放到哪个位置,再枚举 2 放到剩余的哪个位置,最后枚举 3 放到剩余的哪个位置
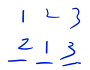
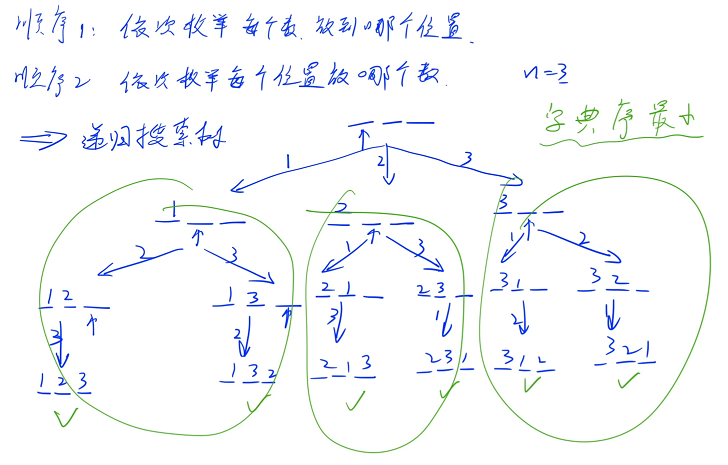
顺序 2:先枚举第一个位置放哪个数,再枚举第二个位置放哪个数. . .下面以顺序 2 为例,给出题目要求 n = 3 的递归搜索树
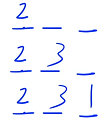
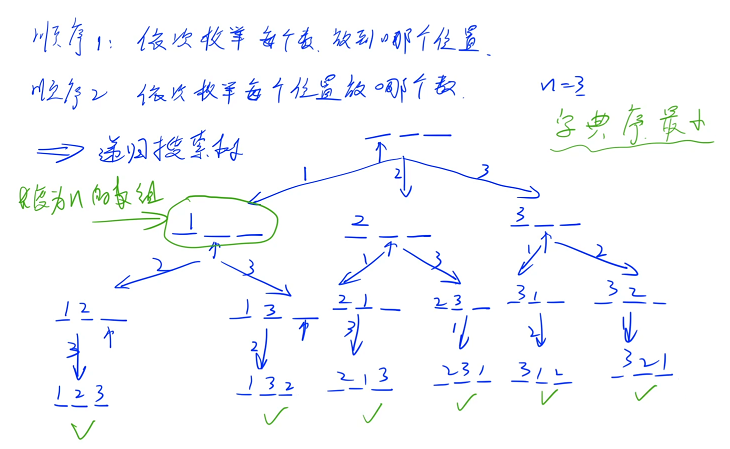
一开始 3 个位置都是空的,依次枚举每个位置放哪个数,第一个位置有 3 种放法,分别可以放 1、2、3,然后枚举第 2 个位置,对于第一个分支来说,1 已经用过了,只剩下 2、3 两个数可以枚举了(可以枚举 2 或者 3),如果枚举 2 的话,就是 1、2、空,接着看第 3 个位置,最后一个位置只有 1 种选法
要输出一个字典序最小的一个方案:
输出字典序最小是什么意思呢?出题人比较懒,如果我们输出任意一个方案,他都要写一个专门的程序来判断这个方案是不是正确的,为了省事,就要求输出字典序最小的方案,方案的顺序就是唯一的,其实我们在做题的时候,只需要注意从小到大枚举每个数,得到的方案就一定是字典序最小的,一般情况下,不需要特殊关注字典序最小这个限制
下面来简单证明一下为什么是正确的:
最终可以通过这样的方式枚举出来一共可以放 6 个分支,每个分支的最后一个节点对应的就是一个方案,一共有 6 种方案
由于是深度优先搜索,在第一个分支里面第一个数是 1 的所有方案的字典序一定小于是 2 的,第一个分支是 2 的所有方案的字典序一定小于是 3 的
在第一个分支里面按照 1、2、3 的顺序来枚举,一定先枚举字典序最小的一部分,再枚举中间的一部分,最后枚举最大的一部分,每一步都是按照这个顺序来枚举,因此我们走到叶节点的顺序也一定是按字典序从小到大走到的
定义一个长度为 n 的数组来记录每个位置当前的状态
变量如果定义成全局变量的话,那么它的初值一定是 0,如果定义成局部变量的话,初值是随机值
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
//N的范围是9 下标从1开始
const int N = 10;
int n;
//st表示当前的状态 0表示还没放数 1~n表示放了哪个数
int state[N];
//在搜索的时候还要保证每个数只用一次 在搜索的时候还要判断当前这个位置可以用的数有哪些 used表示每一个数有没有被用过
//true表示用过 false表示还未用过
bool used[N];
void dfs(int u)
{
//边界
//当u大于n表示枚举完最后一位:当前已经把所有的坑都填满啦
if(u > n)
{
//打印方案
//只需要把每个坑里面的萝卜挨个输出出来就可以了
for(int i = 1;i <= n;i++) printf("%d ",state[i]);
puts("");
return;
}
//枚举当前位置可以填哪些数:每一个分支分别做 从小到大依次枚举每个分支
for(int i = 1;i <= n;i++)
//首先要找出来所有没有用过的数
//如果当前这个数是没有用过的说明当前这个位置可以填这个数
if(!used[i])
{
//当前u位置填这个数
state[u] = i;
//更新状态:true表示这个数被用过了
used[i] = true;
//递归到这个分支里面去处理
dfs(u + 1);
//回来的时候要保证状态已经恢复:恢复现场
state[u] = 0;
used[i] = false;
}
}
int main()
{
scanf("%d",&n);
//当前枚举到第几位
dfs(1);
return 0;
}分析代码的时间复杂度:n × n!
一共会递归 n 层,在第一层的时候有一个 O( n )? 的 for 循环,第二层一共有 n 个分支,每一个分支里面都有一个 for 循环,第三层有 n × (n - 1) 个分支,每一个分支里面都有一个 for 循环. . .以此类推,每一个节点都需要输出一个方案,输出方案也是 O( n ) 的时间复杂度
总共的时间复杂度:n(1 + n + n(n - 1) + n(n - 1)(n - 2) +. . . + n!),下面计算这个括号中的式子大概是什么样的级别( 放缩 )