开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【算法学习】最小生成树 -> 正文阅读

[数据结构与算法]【算法学习】最小生成树

参考算导第三版第23章最小生成树

在电子电路设计中，我们常常需要将多个组件的针脚连接在一起。要连接 $n$ 个针脚，我们可以使用 $n ? 1$ 根连线，每根连线连接两个针脚。显然，我们希望使用的连线长度最短。

可以将上述的布线问题，用一个连通无向图 $G = (V, E)$ 来表示，这里的 $V$ 是针脚的集合， $E$ 是针脚之间的可能连接，并且对于每条边 $\in E$ ，我们为其赋予权重 $w (u, v)$ 作为连接针脚 $u$ 和针脚 $v$ 的代价（也就是连线的长度）。我们希望找到一个无环子集 $T\subseteq E$ ，既能够将所有的结点（针脚）连接起来，又具有最小的权重，即 $\displaystyle \sum_{ (u, v) \in T} w(u, v)$ 的值最小。由于 $T$ 是无环的，并且连通所有的结点，因此 $T$ 必然是一棵树（自由树性质）。我们称这样的树为（图 $G$ 的）生成树，因为它是由图 $G$ 所生成的。我们称求取该生成树的问题为最小生成树问题（这是“最小权重生成树”的简称；例如，我们并不打算将 $T$ 中的边的条数减到最少，因为根据自由树性质，生成树必须恰好有 $∣ V ∣ ? 1$ 条边）。图23-1描述的是一个连通图及其最小生成树的例子。
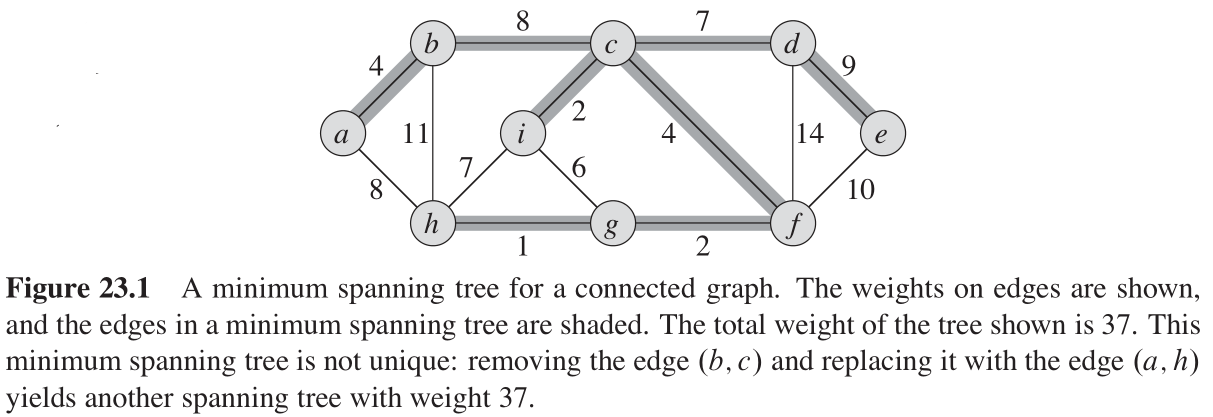
在这里插入图片描述
在这节，我们详细讨论解决最小生成树问题的两种算法：Kruskal 算法和 Prim 算法。如果使用普通的二叉堆，那么可以很容易地将这两个算法的时间复杂度限制在 $\log V)$ 的数量级内。但如果使用斐波那契堆，Prim 算法的运行时间将改善为 $V\log V)$ ，此运行时间在 $∣ V ∣$ 远远小于 $∣ E ∣$ 的情况下、较二叉堆有很大改进。

这里讨论的两种最小生成树算法都是贪心算法。（如算导第16章讨论的）贪心算法的每一步必须在多个可能的选择中选择一种。贪心算法推荐选择在当前看来是最好的选择。这种策略一般并不能保证找到一个全局最优的解决方案。但是，对于最小生成树问题来说，我们可以证明，某些贪心策略确实能找到一棵权重最小的生成树（即算导第16章介绍的理论思想的一种经典应用）。

因为树是图的一种，为了精确起见，在定义树时不仅要用到边，还必须用到结点。虽然这里在讨论树时关注的是它的边，但我们必须留意的是，树 $T$ 中的结点是指由 $T$ 中的边所连接的结点。

1. 最小生成树的形成

假定有一个连通无向图 $G = (V, E)$ 和权重函数 $E\to \R$ ，我们希望找出图 $G$ 的一棵最小生成树，这里讨论的两种算法、都使用贪心策略来解决这个问题，但它们使用贪心策略的方式却有所不同。

这个贪心策略可以用下面的通用方法来表述。该通用方法在每个时刻生长最小生成树的一条边，并在整个策略的实施过程中，管理一个遵守下述循环不变式的边集合 $A$ ：在每遍循环之前， $A$ 是某棵最小生成树的一个子集。

在每一步我们要做的事情是，选择一条边 $(u, v)$ 、将其加入到集合 $A$ 中，使得 $A$ 不违反循环不变式，即 $\cup \{ (u, v) \}$ 也是某棵最小生成树的子集。由于我们可以安全地将这种边加入到集合 $A$ 、而不会破坏 $A$ 的循环不变式，因此称这样的边为集合 $A$ 的安全边 safe edge 。

GENERIC-MST(G, w)
	A = ?
	while A does not form a spanning tree
		find an edge(u, v) that is safe for A
		A = A ∪ {(u, v)}
	return A

我们使用循环不变式的方式如下：

初始化：在算法第 $1$ 行之后，集合 $A$ 直接满足循环不变式（空集是任何集合的子集）。
保持：算法第 $\sim 4$ 行的循环，通过只加入安全边来维持循环不变式。
终止：所有加入到集合 $A$ 中的边都属于某棵最小生成树，因此，算法第 $5$ 行返回的集合 $A$ 必然是一棵最小生成树。

当然，这里的奥妙是算法的第 $3$ 行：找到一条安全边。这条安全边必然存在，因为在执行算法第 $3$ 行时，循环不变式告诉我们存在一棵生成树 $T$ ，满足 $\subseteq T$ 。在第 $\sim 4$ 行的 while 循环体内，集合 $A$ 一定是 $T$ 的真子集。因此，必然存在一条边 $\in T$ ，使得 $\notin A$ ，并且 $(u, v)$ 对于集合 $A$ 是安全的。

在剩下的篇幅里，我们将介绍辨认安全边的规则（定理31.1）。下一节则讨论、使用这条规则来快速找到安全边的两个算法。

我们首先需要一些定义。无向图 $G = (V, E)$ 的一个切割 cut $(S, V ? S)$ 是集合 $V$ 的一个划分，如图23-2所示。如果一条边 $\in E$ 的一个端点位于集合 $S$ ，另一个端点位于集合 $V ? S$ ，则称该条边横跨 cross 切割 $(S, V ? S)$ 。如果集合 $A$ 中不存在横跨该切割的边，则称该切割尊重 respects 集合 $A$ 。在横跨一个切割的所有边中，权重最小的边称为轻量级边 light edge 。注意，轻量级边可能不是唯一的。一般，如果一条边是满足某个性质的所有边中权重最小的，则称该条边是满足给定性质的一条轻量级边。

用来辨认安全边的规则，由下面的定理给出。

定理23.1 设 $G = (V, E)$ 是一个在边 $E$ 上定义了实数值权重函数 $w$ 的连通无向图。设集合 $A$ 为 $E$ 的一个子集，且 $A$ 包括在图 $G$ 的某棵最小生成树中，设 $(S, V ? S)$ 是图 $G$ 中尊重集合 $A$ 的任意一个切割，又设 $(u, v)$ 是横跨切割 $(S, V ? S)$ 的一条轻量级边。那么边 $(u, v)$ 对于集合 $A$ 是安全的。
证明：设 $T$ 是一棵包括 $A$ 的最小生成树，并假定 $T$ 不包含轻量级边 $(u, v)$ ；否则，我们已经证明完毕。现在来构建另一棵最小生成树 $T^{'}$ ，我们通过剪切和粘贴 a cut-and-paste technique 来将 $\cup \{ (u, v) \}$ 包括在树 $T^{'}$ 中，从而证明 $(u, v)$ 对于集合 $A$ 来说是安全的。

边 $(u, v)$ 与「 $T$ 中从结点 $u$ 到结点 $v$ 的简单路径 $p$ 」形成一个环路，如图23-3所示。由于结点 $u$ 和结点 $v$ 分别在切割 $(S, V ? S)$ 的两端， $T$ 中至少有一条边属于简单路径 $p$ 、并且横跨该切割。设 $(x, y)$ 为这样的一条边，因为切割 $(S, V ? S)$ 尊重集合 $A$ ，所以边 $(x, y)$ 不在集合 $A$ 中。由于边 $(x, y)$ 位于 $T$ 中从 $u$ 到 $v$ 的唯一简单路径上，将该条边删除会导致 $T$ 被分解为两个连通向量。将 $(u, v)$ 加上去可将这两个连通分量连接起来、形成一棵新的生成树 $\{ (x, y) \} \cup \{ (u, v) \}$ 。
在这里插入图片描述
下面证明 $T^{'}$ 是一棵最小生成树。由于边 $(u, v)$ 是横跨切割 $(S, V ? S)$ 的一条轻量级边、并且边 $(x, y)$ 也横跨该切割，我们有 $\le w(x, y)$ 。因此， $\le w(T)$

但是， $T$ 是一棵最小生成树，所以有 $\le w(T')$ ；因此， $T^{'}$ 一定也是一棵最小生成树。

下面还需要证明，边 $(u, v)$ 对于集合 $A$ 来说是一条安全边。因为 $\subseteq T$ 并且 $\notin A$ ，所以有 $\subseteq T'$ ；因此 $\cup \{ (u, v) \} \subseteq T'$ 。由于 $T^{'}$ 是最小生成树， $(u, v)$ 对于集合 $A$ 是安全的。 $\blacksquare$

定理23.1能够帮助我们更好地理解、连通图 $G = (V, E)$ 上算法 GENERIC-MST 的工作原理。随着该算法的推进，集合 $A$ 总是保持在无环状态；否则，包含 $A$ 的最小生成树将包含一个环路，这将与树的定义相矛盾。在算法执行的任意时刻，图 $G_A = (V, A)$ 是一个森林， $G_A$ 中的每个连通分量则是一棵树（某些树可能仅包含一个结点，如在算法开始时，集合 $A$ 为空，而森林中包含 $∣ V ∣$ 棵树，每棵树中只有一个结点）。而且，由于 $\cup \{ (u, v) \}$ 必须是无环的，所有对于集合 $A$ 为安全的边 $(u, v)$ 所连接的是 $G_A$ 中不同的连通分量。

GENERIC-MST 算法的第 $\sim 4$ 行的 while 循环，执行的总次数为 $∣ V ∣ ? 1$ 次，因为该循环的每次迭代，都找出最小生成树所需 $∣ V ∣ ? 1$ 条边中的一条。在初始时，当 $\varnothing$ 时， $G_A$ 中有 $∣ V ∣$ 棵树，每次循环将树的数量减少 $1$ 棵。当整个森林仅包含一棵树时，该算法就终止。

（算导23.2节的）下面两个算法将使用定理23.1的下列推论。

推论23.2 设 $G = (V, E)$ 是一个连通无向图，并有定义在边集合 $E$ 上的实数值权重函数 $w$ 。设边集合 $A$ 为 $E$ 的一个子集，且该子集包括在 $G$ 的某棵最小生成树里，并设 $C = (V_C, E_C)$ 为森林 $G_A=(V, A)$ 中的一个连通分量（树）。如果边 $(u, v)$ 是连接 $C$ 和 $G_A$ 中某个其他连通分量的一条轻量级边，则边 $(u, v)$ 对于集合 $A$ 是安全的。
证明：切割 $V_C, V - V_C)$ 尊重集合 $A$ ，边 $(u, v)$ 是横跨该切割的一条轻量级边，因此边 $(u, v)$ 对于集合 $A$ 是安全的。 $\blacksquare$

2. Kruskal 算法和 Prim 算法

这里讨论最小生成树问题的两个经典算法，这两种算法都是前一节讨论的通用算法的细化，每种算法都使用一条具体的规则来确定 GENERIC_MST 算法第三行描述的安全边。

在 Kruskal 算法中，边集合 $A$ 是一个森林，其结点就是给定图的结点（即 $G_A = (V, A)$ ）。每次加入到集合 $A$ 中的安全边，永远是权重最小的、连接两个不同分量的边。
在 Prim 算法中，边集合 $A$ 则是一棵树（同样也有 $G_A = (V, A)$ ），每次加入到 $A$ 中的安全边，永远是连接 $A$ 和 $A$ 之外某个结点（可看作是 $G_A$ 中的另一个连通分量）的边中权重最小的边。

2.1 Kruskal 算法

Kruskal 算法找到安全边的办法是，在所有连接森林的两棵不同树的边中，找到权重最小的边 $(u, v)$ 。设 $C_1, C_2$ 为边 $(u, v)$ 连接的两棵树。由于边 $(u, v)$ 一定是连接 $C_1$ 和其他某棵树的一条轻量级边，推论23.2蕴含：边 $(u, v)$ 是 $C_1$ 的一条安全边。很显然，Kruskal 算法属于贪心算法，因为它每次都选择一条权重最小的边加入到森林。

Kruskal 算法的实现，与（算导21.1节讨论的）计算连通分量的算法类似。我们使用一个不相交集合数据结构来维护几个互不相交的元素集合，每个集合代表当前森林中的一棵树。操作 FIND-SET(u) 用来返回「包含元素 $u$ 的集合」的代表元素。我们可以通过测试 FIND-SET(u) 是否等于 FIND-SET(v) 来判断结点 $u$ 和结点 $v$ 是否属于同一棵树。Kruskal 算法使用 UNION 过程来对两棵树进行合并。

MST-KRUSKAL(G, w)
	A = ?
	for each vertex v in G.V
		MAKE-SET(v)
	sort the edges of G.E into nondecreasing order by weight w
	for each edge(u, v) in G.E, taken in nondecreasing order by weight
		if FIND-SET(v) != FIND-SET(v)
			A = A ∪ {(u, v)}
			UNION(u, v)
	return A

图23-4描述的是 Kruskal 算法的工作过程。算法第 $\sim 3$ 行将集合 $A$ 初始化为一个空集合，并创建 $∣ V ∣$ 棵树，每棵树仅包含一个结点。算法第 $\sim 8$ 行的 for 循环，按照权重从低到高的次序，对每条边逐一进行检查。对于每条边 $(u, v)$ 来说，该循环将检查端点 $u$ 和端点 $v$ 是否属于同一棵树。如果是，该条边不能加入到森林中（否则将形成环路）。如果不是，则两个端点分别属于不同的树，算法第 $7$ 步将把这条边加入到集合 $A$ 中，第 $8$ 行则将两棵树中的结点进行合并。

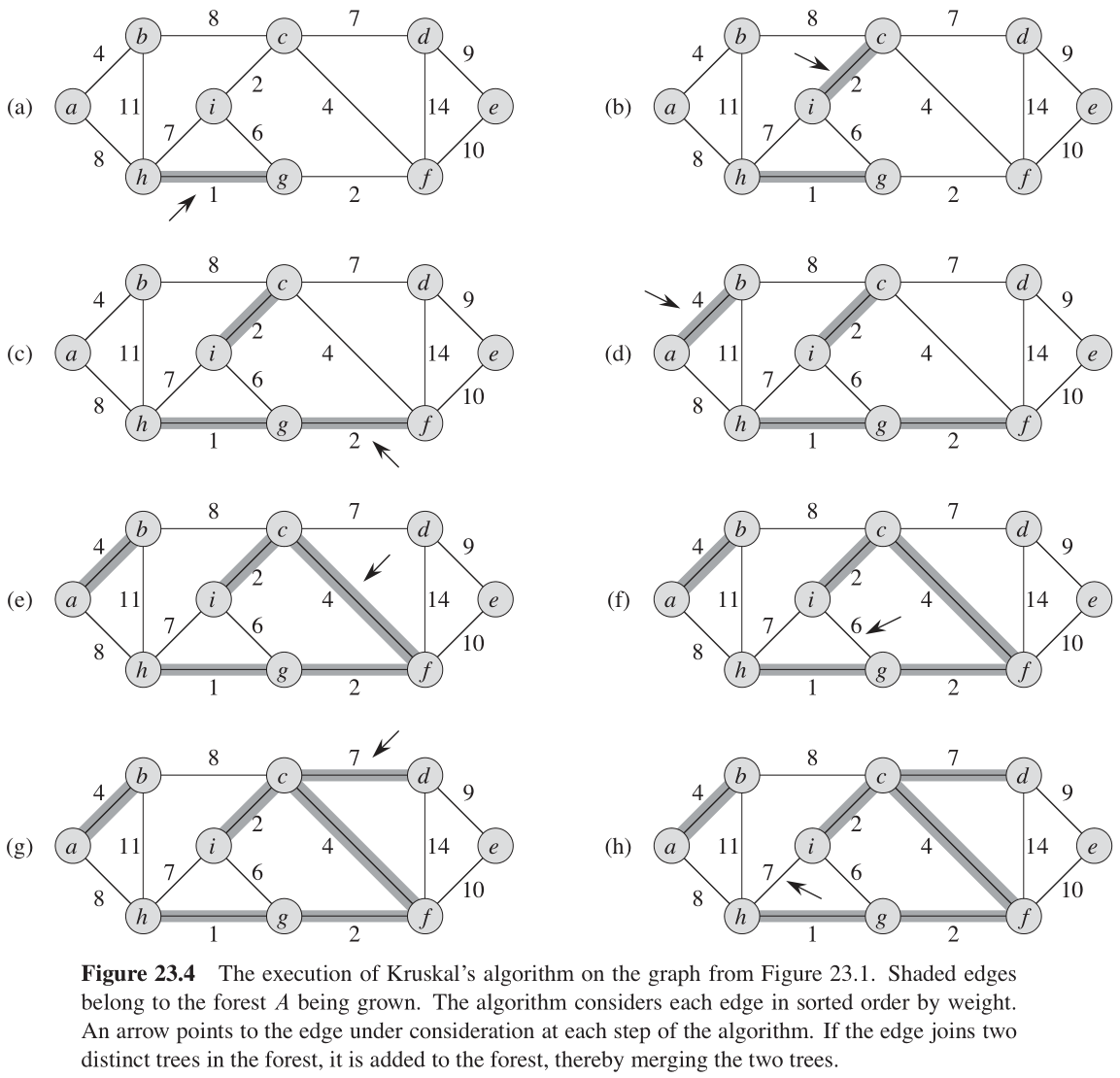
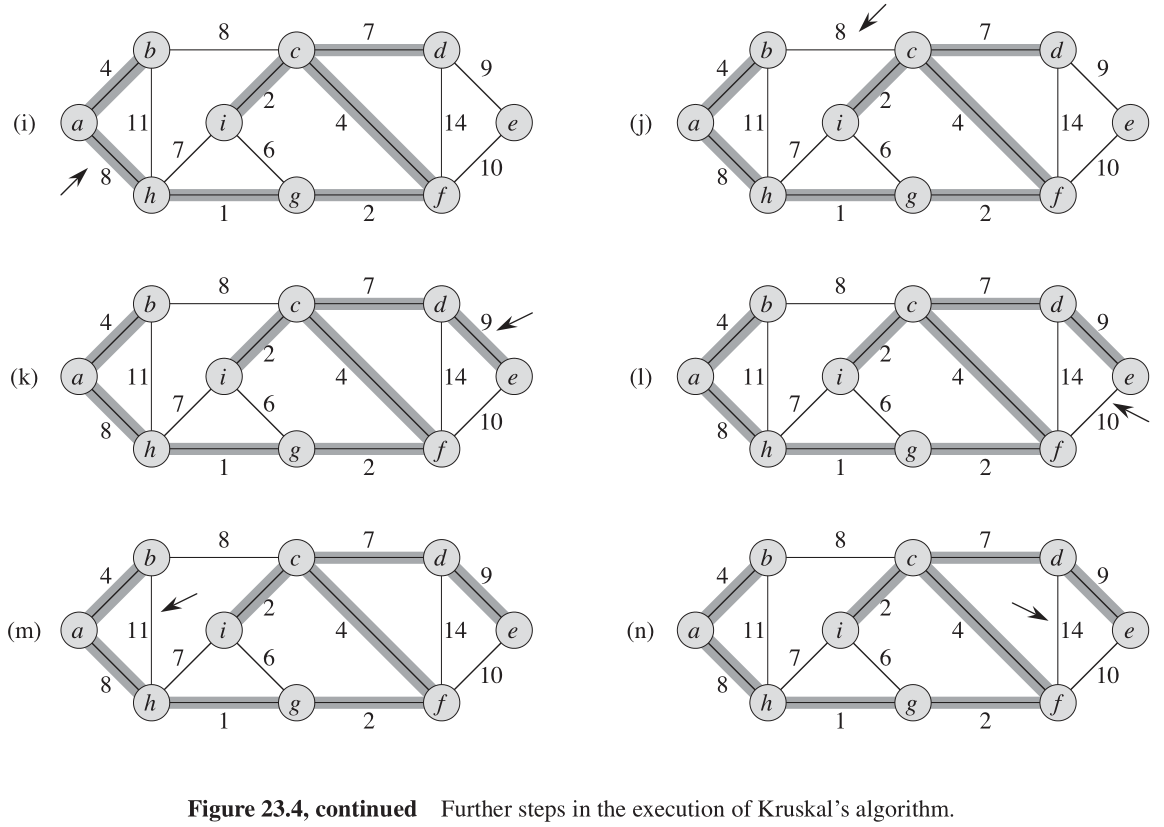
对于图 $G = (V, E)$ ，Kruskal 算法的运行时间依赖于不相交集合数据结构的实现方式。假定使用（算导21.3节讨论的）不相交集合森林实现，并增加按秩合并和路径压缩的功能，因为这是目前已知的渐近时间最快的实现方式。在这种实现模式下，

算法第 $1$ 行对集合 $A$ 的初始化时间为 $O (1)$ ，第 $4$ 行对边进行排序的时间为 $\log E)$ （稍后讨论算法第 $\sim 3$ 行 for 循环中的 $∣ V ∣$ 个 MAKE-SET 操作的代价）。
算法第 $\sim 8$ 行的 for 循环执行 $O (E)$ 个 FIND-SET 和 UNION 操作。与 $∣ V ∣$ 个 MAKE-SET 操作一起，这些操作的总运行时间为 $\alpha(V))$ ，这里 $\alpha$ 是（算导21.4节定义的）一个增长非常缓慢的函数。
由于假定图 $G$ 是连通的，因此有 $\ge |V| - 1$ ，所以不相交集合操作的时间代价为 $\alpha(V))$ 。而且，由于 $\alpha( |V| ) = O(\log V) =O(\log E)$ ，Kruskal 算法的总运行时间为 $\log E)$ 。如果再注意到 $E| < |V|^2$ ，则有 $\log |E| = O(\log V)$ ，因此，我们可以将 Kruskal 算法的时间重新表述为 $\log V)$ 。

2.2 Prim 算法

与 Kruskal 算法类似，Prim 算法也是（算导23.1节讨论的）通用最小生成树算法的一个特例。Prim 算法的工作原理与 Dijkstra 最短路径算法（算导24.3节）相似。Prim 算法具有的一个性质是，集合 $A$ 中的边总是构成一棵树。如图23-5所示，这棵树从一个任意的根结点 $r$ 开始，一直长大到覆盖 $V$ 中的所有结点时为止。
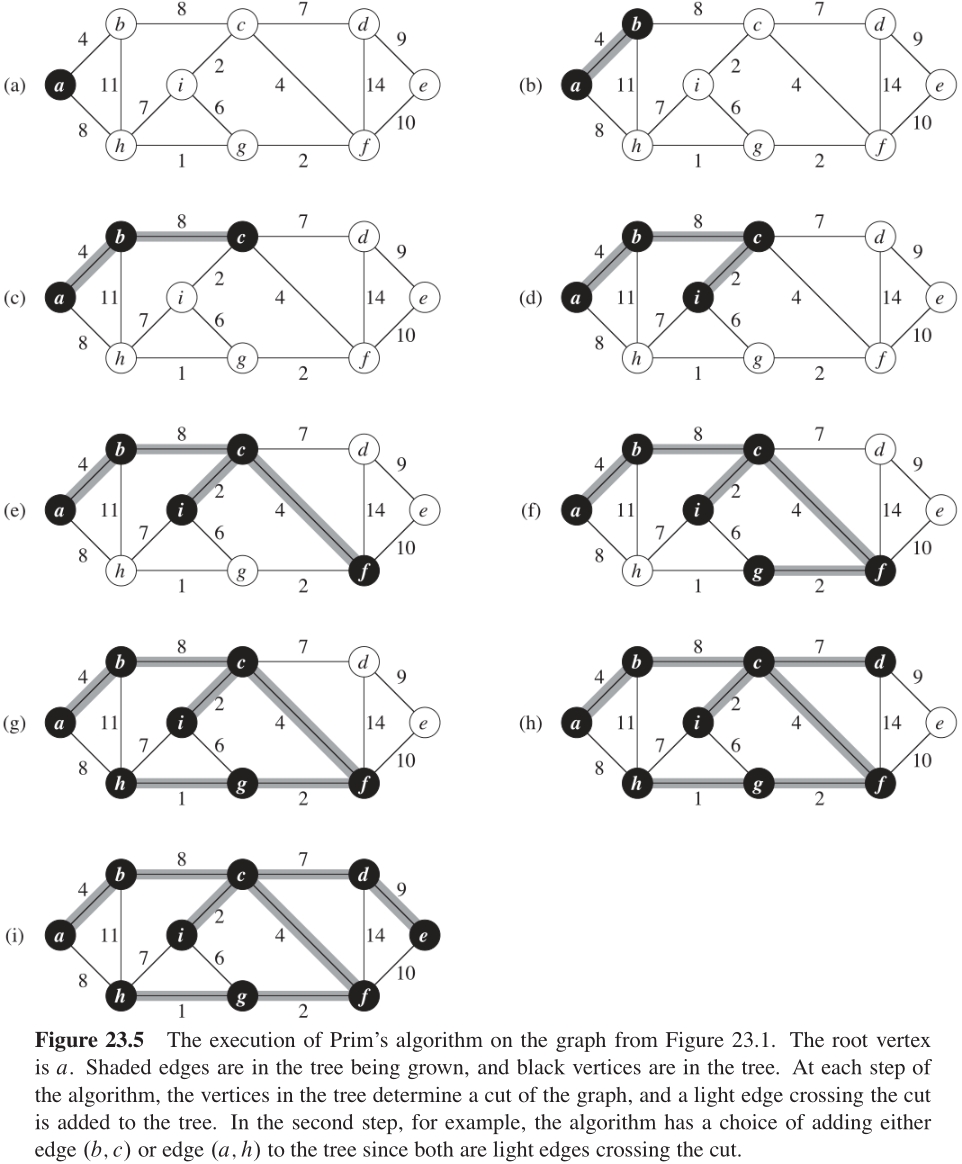
在这里插入图片描述

算法每一步在「连接集合 $A$ 和 $A$ 之外的结点的所有边」中，选择一条轻量级边加入到 $A$ 中。根据推论23.2，这条规则加入的边都是对 $A$ 安全的边。因此，当算法终止时， $A$ 中的边形成一棵最小生成树。本策略也属于贪心策略，因为每一步加入的边都必须是使树的总权重增加量最小的边。

为了有效地实现 Prim 算法，需要一种快速的方法来选择一条新的边，以便加入到由集合 $A$ 中的边构成的树中。在下面的伪码中，连通图 $G$ 和最小生成树的根结点 $r$ 、将作为算法的输入。在算法的执行过程中，所有不在树 $A$ 中的结点，都存放在一个基于 $k e y$ 属性的最小优先队列 $Q$ 中。对于每个结点 $v$ ，属性 $v . k e y$ 保存的是「连接 $v$ 和树中结点的所有边」中最小边的权重。我们约定，如果不存在这样的边，则 $\infin$ 。属性 $v.\pi$ 给出的是结点 $v$ 在树中的父结点。Prim 算法将 GENERIC-MST 中的集合 $A$ 维持在 $\{ (v, v.\pi) \mid v \in V - \{ r \} - Q\}$ 的状态下。

当 Prim 算法终止时，最小优先队列 $Q$ 将为空，而 $G$ 的最小生成树 $A$ 则是：
$\{ ( v, v.\pi) \mid v \in V - \{ r \} \}$

MST-PRIM(G, w, r)
	for each u in G.V
		u.key = INF
		u.π = NULL
	r.key = 0
	Q = G.V
	while Q != ?
		u = EXTRACT-MIN(Q)
		for each v in G.Adj[u]
			if v in Q and w(u, v) < v.key // visited[v]==false
				v.π = u
				v.key = w(u, v)

图23-5描述的是 Prim 算法的工作过程。算法第 $\sim 5$ 行将每个结点的 $k e y$ 值设置为 $\infin$ （除根结点 $r$ 以外，根结点 $r$ 的 $k e y$ 值设置为 $0$ ，以便使该结点成为第一个被处理的结点），将每个结点的父结点设置为 NULL ，并对最小优先队列 $Q$ 进行初始化，使其包含图中所有的结点。该算法维持的循环不变式由三个部分组成，具体阐述如下。

在算法第 $\sim 11$ 行的 while 循环的每次迭代之前，我们有：

$\{ (v, v.\pi) \mid v \in V - \{ r \} - Q\}$
已经加入到最小生成树的结点为集合 $V ? Q$ 。
对于所有的结点 $\in Q$ ，如果 $v.\pi \ne \textrm{NULL}$ ，则 $\infin$ 并且 $v . k e y$ 是连接结点 $v$ 和最小生成树中某个结点的轻量级边 $v.\pi)$ 的权重。

算法第 $7$ 行将找出结点 $\in Q$ ，该结点是某条「横跨切割 $(V ? Q, Q)$ 的轻量级边」的一个端点（第 $1$ 次循环时例外，此时因为算法的第 $4$ 行，所以有 $u = r$ ）。接着将结点 $u$ 从队列 $Q$ 中删除，并将其加入到集合 $V ? Q$ 中，也就是将边 $u.\pi)$ 加入到集合 $A$ 中。算法第 $\sim 11$ 行的 for 循环，将每个与 $u$ 邻接、但却不在树中的结点 $v$ 的 $k e y$ 和 $\pi$ 属性进行更新，从而维持循环不变式的第 $3$ 部分成立。

Prim 算法的运行时间取决于最小优先队列 $Q$ 的实现方式。如果将 $Q$ 实现为一个二叉最小优先队列（参考算导第 $6$ 章）：

我们可以用 BUILD-MIN-HEAP 来执行算法第 $\sim 5$ 行，时间成本为 $O (V)$ 。
while 循环中的语句一共要执行 $∣ V ∣$ 次，由于每个 EXTRACT-MIN 操作需要的时间成本为 $O(\log V)$ ，EXTRACT-MIN 操作的总时间为 $O(V\log V)$ 。
由于所有邻接链表的长度之和为 $2 ∣ E ∣$ ，算法第 $\sim 11$ 行的 for 循环的总执行次数为 $O (E)$ 。在 for 循环里面，我们可以在常数时间内、完成对一个结点是否属于队列 $Q$ 的判断，方法就是对每个结点维护一个标志位、来指明该结点是否属于 $Q$ ，并在将结点从 $Q$ 中删除时、对该标志位进行更新。算法第 $11$ 行的赋值操作，涉及一个隐含的 DECREASE-KEY 操作，该操作在二叉最小堆上执行的时间成本为 $O(\log V)$ 。
因此，Prim 算法的总时间代价为 $\log V+ E\log V) = O(E \log V)$ 。从渐近意义上说，它与 Kruskal 算法的运行时间相同。

如果使用斐波那契堆来实现最小优先队列 $Q$ ，Prim 算法的渐近运行时间可得到进一步改善。（算导第19章告诉我们）如果斐波那契堆中有 $∣ V ∣$ 个元素，则 EXTRACT-MIN 操作的时间摊还代价为 $O(\log V)$ ，而 DECREASE-KEY 操作（实现算法第 $11$ 行的操作）的摊还时间代价为 $O (1)$ 。因此，如果使用斐波那契堆来实现最小优先队列 $Q$ ，则 Prim 算法的运行时间将改进到 $V\log V)$ 。