🚀 优质资源分享 🚀
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| 🧡 Python实战微信订餐小程序 🧡 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| 💛Python量化交易实战💛 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
动态规划解0-1背包问题
动态规划解0-1背包问题是一个十分典型案例,我从网上查询好多相关资料,但是大部分都深奥难懂,并不适合初学算法的小白,其中涉及的递推关系式、填表,以及最后的二维表简化为一维表的优化过程,好多都是一笔带过,所以,今天就尽我所能,来叙述一下对于0-1背包问题使用动态规划来求解。
要解决0-1背包问题,首先咱们要解决的是什么是动态规划。
动态规划
先说一说什么是动态规划。
动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
这里又涉及到分治算法,那就简单概述一下分治算法。
分治算法简而言之就是将一个大问题分成若干个小问题,通过求解小问题的最优解,进而推出所求解问题的最优解。
这么乍一看,可能会觉得分治算法与动态规划相类似,实际上,他们有一个最本质的区别,那就是子问题的类型不同。
分治算法的子问题是相互独立的,子问题与子问题之间并没有什么关联。而动态规划的子问题就有意思了,他们是重叠的子问题。这么单纯的用文字来描述可能有点难以理解,我们借用一张图来声明
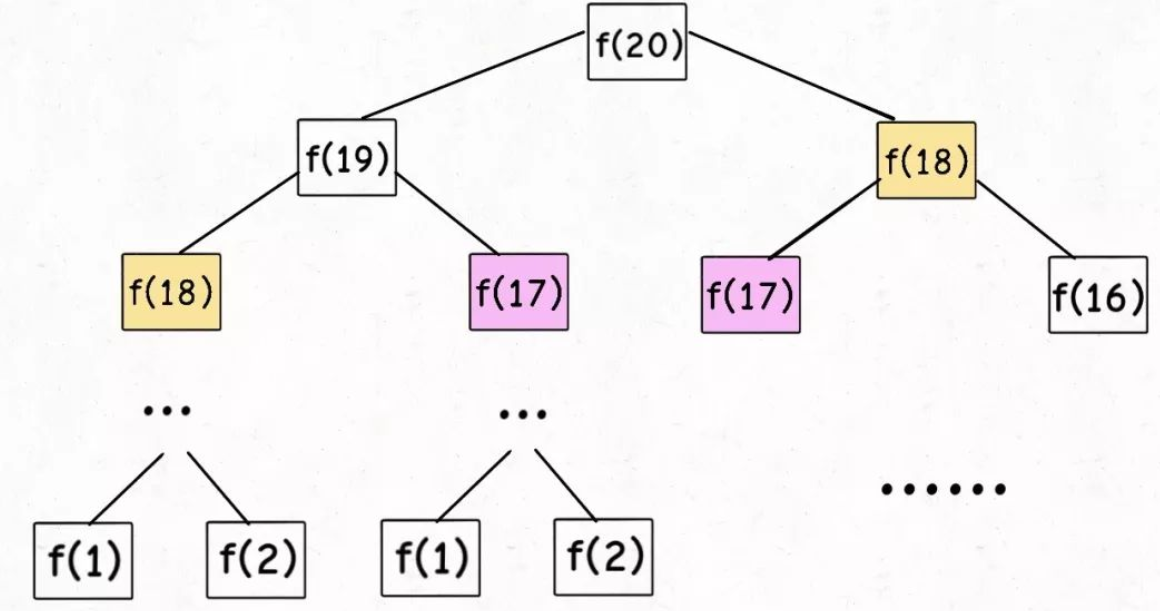
从这张图我们可以看出,当我们对所求问题进行子问题划分时,会产生很对相同的子问题,这些子问题在计算机中我们已经求得结果一次,再另一个子问题中,我们如果再让计算机求解相同的子问题,显然有点不太地道。
而这种一遍一遍求解相同子问题,如果当问题为n时,显然我们付出的时间是相当大的。
为了解决这个问题,动态规划表示,可以用一张数组来记录下我们之前已经求解的子问题结果,当我们再次调用时,只需先从数组中查询是否有所求子问题的结果,如果有,皆大欢喜,直接把答案调出来使用,如果没有,就将该问题的解存储进去,为了下一次查询提供结果。
这么看来,我们就是在用空间换时间,实际上就是如此。
简单来说,求解动态规划的核心是穷举,因为要求最值,所以要把所有可行的答案穷举出来,然后在其中找最值。而在我们穷举的过程中,我们会把碰到的解相同的子问题用一个数组记录下来。
通过上述所言,我们讲清楚了什么是动态规划。
进而,我们可以总结出,要想使用动态规划,我们的问题必不可少两个基本要素是:
- 最优子结构性质
- 重叠子问题
当我们的问题具备这两个基本要素后,我们便可以考虑使用动态规划来求解问题。
0-1背包问题
实现我们来了解一下什么是0-1背包问题。
在学习到动态规划算法之前,相想必我们也接触过贪心算法。
而在贪心算法中,我们也肯定接触过一个经典案例,那就是用贪心算法求解背包问题。
没接触过也没有关系,我们只是用贪心算法解背包问题来类比一下,所以我们只需要了解用贪心算法解决背包问题的大体思路
用贪心算法解背包问题的基本步骤: 首先计算每种物品单位重量的价值v[i]/w[i],然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直地进行下去,直到背包装满为止。
贪心算法解决背包问题,无疑是一种十分方便的方法,但是在0-1背包问题中,我们增加了一条限制,就是我们并不能取得平均价值,比如说一个苹果重5斤,价值是5,平均价值是1,但是当背包还剩下2斤的容量时,我们不可能装下2/5个苹果,所以,就衍生出来了我们的0-1背包问题:
有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?

那么我们就来解决一下这个不可分割的背包问题。
解题之前先要梳理思路,该题的思路是一般动态规划的解题思路,就是将大问题化成子问题,然后动态填表的过程。而该题的核心是如何动态填表。
背包问题抽象化
把背包问题抽象化,Vi表示第 i 个物品的价值,Wj表示第 i 个物品的体积(重量),设dp[i][j]为背包为j时前i个物品的总价值。
也就是说,dp[1]2]的值就是我们背包为2时,装入第一个物品时的总价值。
在这里不得不说一句,我们的i,j最好是从1开始取值,因为在我们的递推方程中,我们可以看到[j-1],[i-1],这时如果我们从0开始取值,我们就会发现出现数组越界的现象。
在这里可能会很难看出我们的状态转移方程,我们不妨打表来推出我们的dp数组。(dp就是我们的递推数组,i表示物品,j表示背包容量,dp值为总价值)
这样我们就可以通过打表:
首先初始化边界,dp(0,j)=dp(i,0)=0由于我们会用到dp[i-1][j-1],如果我们的i,j从0开始迭代,就容易出现越界,所以这里我们通常迭代从1开始。

W0-W4是物品编号,M0-M8是背包的容量,表中绿色区域表示dp值,即该背包容量下,前n个物品可装入的最大价值。

通过打表,当我们打到M3,W2时,我们发现一个问题,就是在dp[2][3],我们有两种选择:即容量为3,我们可以选W2,也可以选择W1,因为dp为可装入物品的价值的最大值,这是我们需要比较W1与W2的价值,选择价值大的一个,如果价值W2>W1,则dp[2][3]=W2的价值,否则dp的值是W1的价值,在此时,我们可以看到W2>W1,所以我们填入W2的价值。
如此继续打表

我们可以看到,当我们的背包容量不足以装下新的物品时,实际上它的值是相同背包容量下,前n-1个物品的最大价值。即dp[i][j]=dp[i-1][j];
当可以装下新加入的物品时,得到新的dp递推公式。
但是在得到递推公式之前我们需要知道,我们的dp[i][j]值是最大值,也就是说。我们需要比较,即max(dp[i][j-wi]+新物品的价值,dp[i-1][j]),取最值。
这样,通过打表的方式,我们得到了递推公式。
做到这里,我们就已经将0-1背包问题解决。
接下来我们来实现代码
int W[30],C[30];//w是物品重量,C是物品价值,测试数量不能超过30
int main()
{
int,m,n;//m为背包容量,n为物品数量
scanf("%d%d",&m&n);
for(int i=0;iscanf("%d%d",&w[i]&c[i]);
}
for(int i = 1;i<=n;i++){
for(int j =1;j<=m;j++){
if(j>w[i]){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+c[i]);
}
}
}
}
代码优化
通过代码,我们实现了动态规划解决0-1背包问题。但是我们不难发现,这样通过一个二维表十分的浪费空间,我们可不可以优化代码呢。
我们来看递推公式,不难发现,实际上,
dp二维表可以化为一维表。
j > w[i]时,dp[i]=dp[i-1]
j < w[i]时,dp[j] = dp[j - w[i]] + v[i];
#include
int main() {
//动态规划解0-1背包问题
//递推公式:dp[j]=dp[j-w[i]]+v[i]
int m, n;//m为背包容量,n为物品数量,n小于20;
int w[20], v[20],dp[20];//w[i]为第i件物品的重量,v[i]是第i件物品的价值,dp[]为递推数组
scanf("%d %d", &m, &n); //m为背包容量,n为物品数量,n小于20;
for (int j = 0; j<= m; j++) {
dp[j] = 0; //dp置零
}
for (int i = 1; i <= n; i++) {
scanf("%d %d", &w[i], &v[i]);
}
for (int i = 1; i <= n; i++) {
for (int j = m; j >= 0; j--) {
if (j >= w[i]) {
dp[j] = dp[j - w[i]] + v[i];
}
}
}
printf("%d", dp[m]);
return 0;
}
由此我们用动态规划将0-1背包问题讲了个大概。
