开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 分支限界及其应用 -> 正文阅读

[数据结构与算法]分支限界及其应用

分支限界是回溯方法的一种改进，从另一个角度来看背包问题可以理解为它是一个组合优化的问题，在搜索解空间中找到满足约束条件的解，使得目标函数达到极大极小，这个地方在搜索的时候，其实是可以考虑对回溯的空间做一个约束。

一、组合优化问题

除了满足约束以外，还可以做一点事情：对求最大和求最小这种优化问题（前提必须是优化问题，如果是判定问题不适用于分支限界），在做分支的时候，往下进行空间展开的时候，可以做早先的判定，判定可能性和潜力。

以背包问题为例，背包问题是要找到一个价值的最大化，背包问题和剩余的空间量有关，什么是代价函数，什么是潜力。

在背包里面装物体的时候，背包现在剩余的空间，也就是说，这些空间是装还有没有装到的物品，剩余的空间如果全部拿来装入单位价值重量最大的那个，这就是一个潜力的问题。

用这个空间来乘单位最大物品的价值，这个东西我们称之为潜力，也就是它的可能性，也就是可能性有多大，潜力只能小于等于它，背包问题里面，可以早一点的去判定，这个背包最多剩下的空间能够达到最大的可能性是多大，可以把它找出来，找到这个潜力以后，把这个东西称为代价函数（当然每个教科书上有不同的叫法）。

代价函数意味着这个点还往下搜索吗？还往下找的可能必要性在于往下找能找到一个更好的，找到一个更好的解，更好的价值，更大的空间（装法），但是现在早一点判定，没有办法去找一点更大的，因为潜力已经到这里了。

潜力的含义是：当这个背包，剩余空间如果全部拿来装剩下的物品里面的单位重量最大价值的物品，塞进去以后这个值一定是剩下的可能性的最大，因此把代价函数计算出来之后和已知的解对比，搜索一个解之后记录下来当前的最大价值，接下来搜索另一个分支，判断这个分支走到这个地方的时候，潜力是多大，如果这个潜力没有已经找到的那个解好，那么这个时候还有没有必要继续搜索这一部分空间，还是用回溯算法来讲解，回溯算法在寻找这个空间的时候，优化问题有些空间的搜索，不仅仅是满足约束这么简单，还可以考虑它的潜力有多大，如果潜力已经挖掘到极限了，没有办法达到更大了，也不再搜索了，也就是把它去掉，从挖掘潜力的角度（另外一个角度），来规避掉删除缩小搜索空间，这个是另外一种从代价函数的角度，这个叫做分支限界。

分支限界说的事情就是目标函数达到最大最小，当然是个优化问题，针对这一类的问题，可以在搜索空间的结点对每个结点做一个潜力值，这个潜力值可以把它称之为代价，在不同的问题里有不同的计算方式，但是代表的含义就是这个含义，也就是说下面的这些路径搜索，它的最大的可能性或者最好的可能性有没有可能超过已知的解，在回溯的过程中，一开始是没有找到一个解的，但是运气好，在搜索过程找到一个解，结束了把解记录下来了，这个解就是一种装法，比如说背包问题，已经找到一种装法，这种装法已经有一个价值了，接下来要做的事情，看一看这边不同的搜索分支，每一个搜索分支的潜力，有没有可能超过它，这个潜力有多大，如果有可能超过它来做搜索，如果没可能就不做搜索，那这个可能是如何计算的呢？在背包问题里是很好算的，因为背包问题比较特殊，容易计算。其他的问题也可以类似的去设计，背包问题，背包总的重量，当装入物品后就会有剩余空间，剩余空间，剩余重量，来装哪些？去装哪些还可以再装的物品，还可以再装物品里面的单位重量最大价值的那个物品，把这个物品全部装进去，这个地方本身就是一种不可能，物品也不能可能是随意多的，比如0-1背包就一个，但是强调可以去估计最大值，就可以理想化，（1）就认为这个物品，是可以切的，（2）认为这个物品是无限多的，所以在估计潜力的时候，就可以用最大的值来做计算。

前提：在用代价函数做计算，首先对单位重量的价值做一个排序，钻石黄金比普通的钢铁石头要有价值，这个说的是单位重量来衡量价值更大一些，所以一开始为了估计剩余的可能性，先装单位重量价值大的，后装单位重量价值小的物品。

二、实例

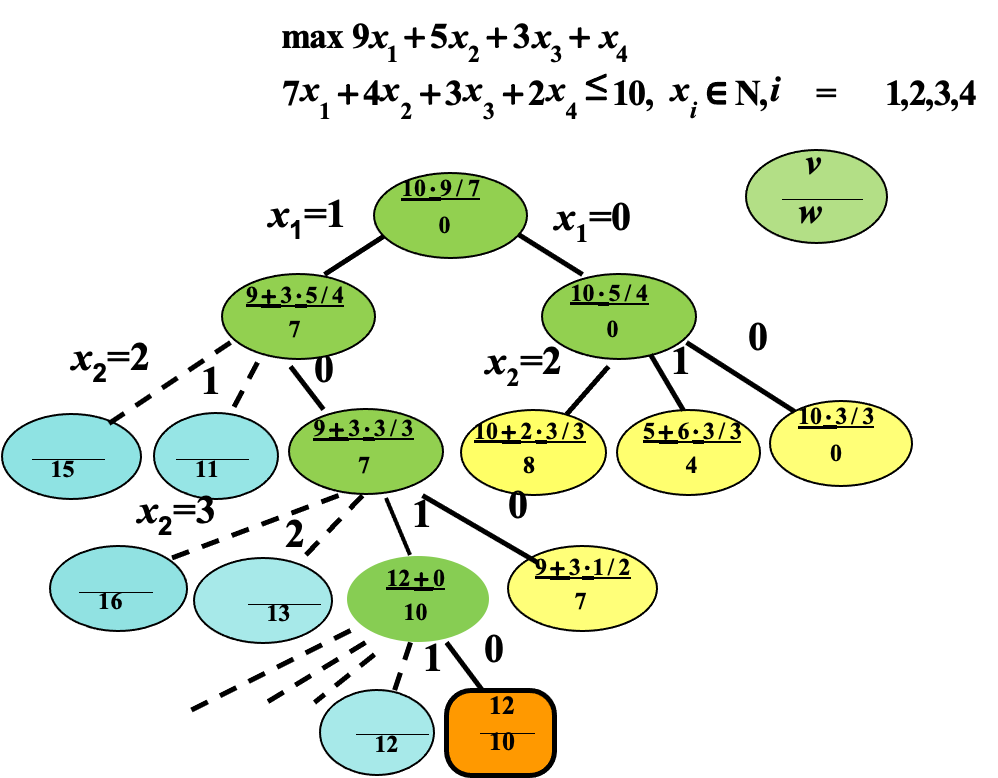
在这里插入图片描述

先考虑贵重的物品，再考虑廉价的物品，这样子便于做估计，这个问题和普通的背包不一样的地方在于首先对物品排序，先将每个物品单位重量价值大的排在前面，也就是用value / weight，接下来排完序以后，对单位重量价值最大的物品对它先装（其实也是一个搜索的过程），刚开始背包没有任何重量没有装任何物品、总重量是零，它的value的可能性，因为总的约束是10，用10 * （7/9）注：7/9对于所有物品而言，这个7/9就是钻石，单位重量价值最大的 假如这个钻石是可以切成粉末的往里面塞，这样的一种估计，估计完之后往里面装，装进去以后，背包目前已经占据7个空间，因为这个一个物品装进去了，装进去之后它的价值是9，在算一下可能性，由剩余的背包的容量是3 *（5/4），接下来再考虑在这种可能下一种物品能不能往里面装的问题。可以看出横线的上方始终是有一个值的，这个值以前是不存在的，算可能性的目的，将物品1、3装进去发现一个可行解这个地方就是9+3

最开始其实在做搜索，在搜索的时候不考虑空间装或者不装（0-1背包），这个背包当你装入一些物品以后，那么肯定会有一些剩余量（剩余空间），剩余的空间肯定是装剩下的物品的，用剩余的空间量来乘剩下的物品，最金贵的物品（单位价值量最大的物品），估计剩余空间潜力。

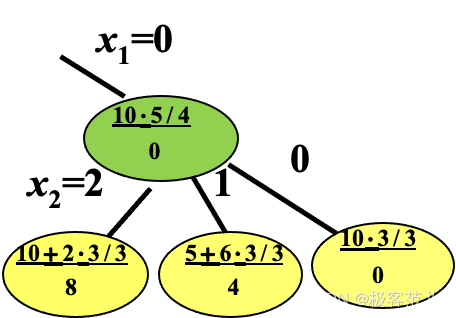
在这里插入图片描述

剩余的重量乘单位价值最重的物品，把剩余的潜力估计出来，估计出来就写在横线上面，接下来再做搜索，发现这个地方第一个物品如果不装，这个路径在搜素的时候发现这个地方有一个值10 * （5/4）这个值超过你算出来的这个可能性接下来就不再搜索，再往下搜索的结点最大的可能性已经小于12了。小于已经找到的那个路径，一个可行解，这个解还不确定是不是最优的，但是已经找到一个了，找到以后这就作为一个基准，如果后面的可能性不会超过它，后面的东西都统统删掉，不可能再去搜索了。