信号模型
线性调频信号具有一个优势,那就是不减小脉宽的情况下,同样能够提高雷达的分辨力。
现代雷达普遍采用线性调频体制,了解线性调频雷达信号很重要。
一般情况下,线性调频雷达信号,定义为
s
~
(
t
)
=
r
e
c
t
(
t
τ
)
e
x
p
[
j
2
π
(
f
c
t
+
1
2
μ
t
2
)
]
(1)
\tilde{s}(t)=rect(\frac{t}{\tau})\mathrm{exp}[j2\pi (f_ct+\frac{1}{2}\mu t^2)] \tag{1}
s~(t)=rect(τt?)exp[j2π(fc?t+21?μt2)](1)
式(1)中,
r
e
c
t
(
t
)
rect(t)
rect(t)为矩形脉冲,其归一化为
r
e
c
t
(
t
τ
)
=
{
1
0
≤
t
≤
1
0
t
>
1
,
t
<
0
(2)
rect(\frac{t}{\tau})=\begin{cases} 1 \qquad 0\le t \le 1 \\ 0 \qquad t>1,t<0 \end{cases} \tag{2}
rect(τt?)={10≤t≤10t>1,t<0?(2)
f
c
f_c
fc?为雷达信号的载频,、
μ
\mu
μ为调频斜率,
μ
=
B
/
τ
\mu =B/\tau
μ=B/τ,
B
B
B为雷达信号的带宽。
复数形式的信号模型
在雷达信号处理中,经常采用复数形式,这是因为雷达接收机往往采用的是IQ解调。雷达信号往往是窄带的,复数形式的线性调频信号可以表示为:
s
~
(
t
)
=
r
e
c
t
(
t
τ
)
e
x
p
[
j
2
π
(
f
c
t
+
1
2
μ
t
2
)
]
=
r
e
c
t
(
t
τ
)
e
x
p
(
j
π
μ
t
2
)
e
x
p
(
j
2
π
f
c
t
)
=
s
(
t
)
e
x
p
(
j
2
π
f
c
t
)
(3)
\tilde{s}(t)=rect(\frac{t}{\tau})\mathrm{exp}[j2\pi (f_ct+\frac{1}{2}\mu t^2)] \\ = rect(\frac{t}{\tau})\mathrm{exp}(j\pi \mu t^2)\mathrm{exp}(j2\pi f_c t)\\ \tag{3} =s(t)\mathrm{exp}(j2\pi f_c t)
s~(t)=rect(τt?)exp[j2π(fc?t+21?μt2)]=rect(τt?)exp(jπμt2)exp(j2πfc?t)=s(t)exp(j2πfc?t)(3)
式(3)中
s
(
t
)
s(t)
s(t)被称为复包络,注意这个
s
s
s上面没有波浪线了,
e
x
p
(
j
2
π
f
c
t
)
\mathrm{exp}(j2\pi f_c t)
exp(j2πfc?t)被称为复载频。由于复载频是不包含有信息的,因此在信号处理中我们可以把它忽略掉。
信号仿真
编程实现一下,可以加深理解,巩固已有的概念,同时也是在强迫自己输出。
仿真参数如下:
- 采样率 f s = 30 f_s=30 fs?=30MHz;
- 脉宽 τ = 10 μ s \tau=10\mu s τ=10μs;
- 脉冲重复周期 P R I = 100 μ s PRI=100\mu s PRI=100μs;
- 带宽B=10MHz;
下面是matlab仿真代码:
%% 线性调频信号仿真
% 2022.5.26
clear all; close all; clc;
%% 仿真参数设置
T = 100e-6; % 仿真时长
PRI = 100e-6;% 脉冲重复周期100us
tau = 10e-6; % 脉冲宽度为10us
fs = 30e6; % 采样率30MHz
B = 10e6; % 信号带宽为10MHz
%% 计算参数
dutyCy = tau/PRI; % 脉冲占空比
fr = 1/PRI; % 脉冲重复频率
dt = 1/fs; % 采样间隔
t = 0:dt:T-dt; % 时间刻度向量
mu = B/tau; % 调频斜率
%% 线性调频信号
s = exp(j*pi*mu*t.*t); %线性调频信号
%% 脉冲调制
x=square(2*pi*fr*t,dutyCy*100)./2+0.5; % 未调制的脉冲信号
sHat = x.*s;
%% 绘图
plot(t,x.*s)

我们可以只仿真脉冲内的信号,调整一下仿真时长即可,仿真时间长度就等于脉冲宽度,并且也不需要将线性调频信号和门函数相乘。
%%仅仅仿真了脉冲宽度内的调频信号
% 2022.5.27
clear all; close all; clc;
%% 仿真参数设置
T = 10e-6; % 仿真时长等于脉冲宽度10us
PRI = 100e-6;% 脉冲重复周期100us
tau = 10e-6; % 脉冲宽度为10us
fs = 30e6; % 采样率30MHz
B = 10e6; % 信号带宽为10MHz
%% 计算参数
dutyCy = tau/PRI; % 脉冲占空比
fr = 1/PRI; % 脉冲重复频率
dt = 1/fs; % 采样间隔
t = 0:dt:T-dt; % 时间刻度向量
mu = B/tau; % 调频斜率
N = length(t); %序列长度
%% 线性调频信号
s = exp(j*pi*mu*t.*t); %线性调频信号
% %% 脉冲调制
% x=square(2*pi*fr*t,dutyCy*100)./2+0.5; % 未调制的脉冲信号
%% 频域分析
S = (fft(s))*2/N; %进行fft
amplitudeS = abs(S); % 幅度谱
normAmpliS = amplitudeS./max(amplitudeS); % 幅度谱进行归一化
%% 绘图
figure
plot(t,real(s))
xlabel('时间/us');
ylabel('归一化幅度');
figure
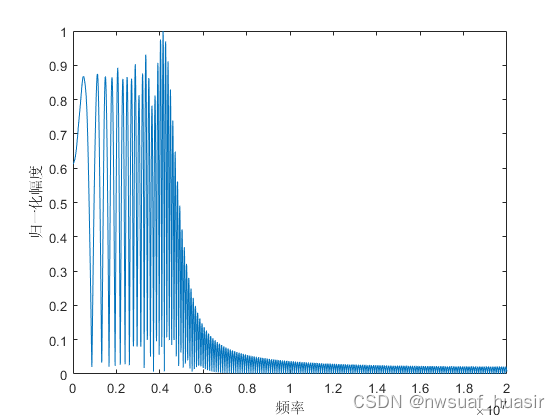
plot(0:(fs/N):(fs/2-fs/N),normAmpliS(1:floor(N/2)))
xlabel('频率/MHz');
ylabel('归一化幅度');

频域分析:

线性调频信号仿真探究
看到一些仿真,是将信号载频 f c f_c fc?当作中频对待,那么基带信号的顺时频率便是 ( ? B / 2 , B / 2 ) (-B/2,B/2) (?B/2,B/2)。这时候该怎么仿真呢?只需要将线性调频信号的时间 t t t设置为 ( ? T / 2 , T / 2 ) (-T/2,T/2) (?T/2,T/2)即可。
%% 线性调频信号仿真
%%仿真了线性调频信号
%%fc为中频
% 2022.5.26
clear all; close all; clc;
%% 仿真参数设置
T = 100e-6; % 仿真时长等于脉冲宽度100us
PRI = 100e-6;% 脉冲重复周期100us
tau = 10e-6; % 脉冲宽度为10us
fs = 40e6; % 采样率30MHz
B = 10e6; % 信号带宽为10MHz
JSR = 20; % 干信比为20 dB
%% 计算参数
dutyCy = tau/PRI; % 脉冲占空比
fr = 1/PRI; % 脉冲重复频率
dt = 1/fs; % 采样间隔
tt = 0:dt:T-dt; % 整个脉冲周期PRI
t = -tau/2:dt:tau/2-dt; % 脉冲宽度时间刻度向量,从负到正
matchFt = 0:dt:tau-dt;
mu = B/tau; % 调频斜率
N = length(tt); % 序总列长度
Npri = length(t); % 线性调频信号脉冲内的长度
%% 线性调频信号
s = exp(j*pi*mu*t.*t); % 线性调频信号(仅脉冲内)
x = zeros(1,N); % 一个完整的PRI信号预设变量
x(1:Npri) = s; % 添加脉冲内的线性调频信号
%% 脉冲调制
% 匹配滤波器单位冲击响应
h = exp(-j*pi*mu*t.*t); %匹配滤波器单位冲击响应
so = conv(x,h); % 卷积实现匹配滤波
%% 频域分析
S = real(x);
S = ((fft(S)))*2/N; %进行fft
amplitudeS = abs(S); % 幅度谱
normAmpliS = amplitudeS./max(amplitudeS); % 幅度谱进行归一化
%% 绘图
figure
plot(real(s)./max(real(s)))
xlabel('时间/us');
ylabel('归一化幅度');
figure
plot(real(x))
xlabel('时间/us');
ylabel('归一化幅度');
figure
plot(0:(fs/N):(fs/2-fs/N),normAmpliS(1:floor(N/2))) %幅度谱
xlabel('频率/MHz');
ylabel('归一化幅度');