地球的正常重力场
定义
在地球的大地水准体描述中,水准体表面是地球实际重力场的一个等位面,每一点的重力方向均与该点所在等位面相垂直,实际的重力方向一般称为天文垂线,或称真垂线。由于实际地球内部密度分布不均匀,并且表面凹凸不平,大地水准面不规则﹐所以实际水准面上重力的大小和方向也不规则。与地球的几何形状描述类似,也希望使用一个简单的数学函数来拟合地球重力场,这个简单函数表示的重力场就称为正常重力场。
图解
如下图所示,地球上某一点的重力是地球万有引力与离心力共同作用的结果
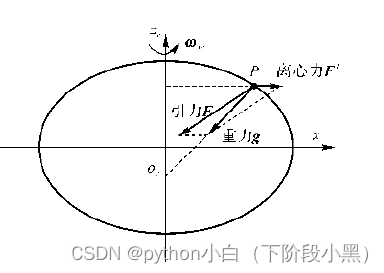
圆球假设下的地球重力
若将地球视为圆球体并且认为密度均匀分布﹐那么地球引力指向地心,可推导得公式:
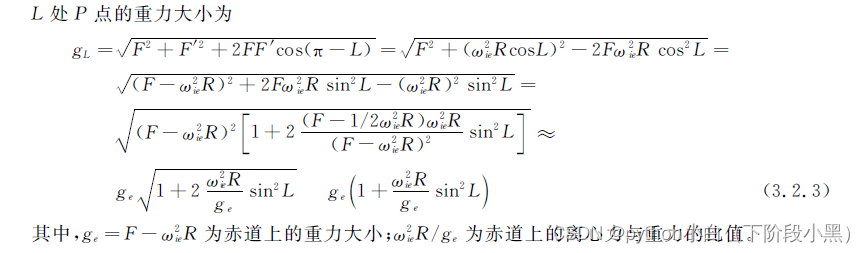
旋转椭球假设下的地球重力
对于地球的旋转椭球体描述,假设在椭球表面上的重力矢量处处垂直于表面,也就是说,旋转椭球表面为重力的一个等位面
历史上重要的正常重力模型
(1)1901年,德国人赫尔默特(F.R. Helmert)根据当时波斯坦系统的几千个重力测量结果,给出正常重力公式为

(2)1909年,美国人海福特(J.F.Hayford)根据美国当时的大地测量结果给出了一个参考椭球,它的赤道半径为R=6378 388 m,几何扁率为f=1/297.0;1928年,芬兰人海斯卡宁(W. A. Heiskanen)根据当时的重力测量结果计算出正常地球模型在赤道上的重力为9.78049m/s2

1930年,国际大地测量与地球物理联合会(IUGG)将上式定为国际正常重力公式。
(3)利用现代卫星测量技术,IUGG于1979年通过了1980大地参考系﹐与其对应的正常重力公式为
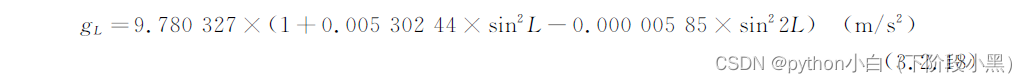
(4)1987年,WGS-84(World Geodetic System 1984)大地坐标系给出的地球参数为

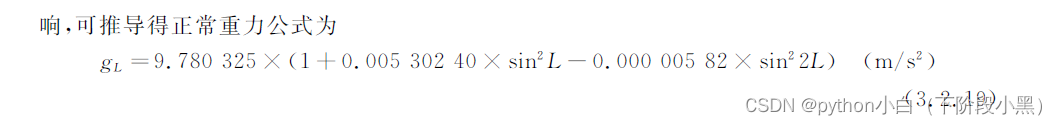
重力与高度的关系
在惯性导航系统中常涉及椭球高,海拔高和气压高等几种高度的测量和计算,它们之间存在一定的差别:
①椭球高度又叫大地高,指在一定的地球椭球模型下,被测点与其在椭球面上投影之间的距离,椭球高是一个纯粹的几何概念,选择的椭球模型不同高度也不一样;
②海拔高度也称绝对高度,它是被测点高出大地水准面的垂直距离;
③气压高度是通过测量大气压力而实现的,海拔高度上升,气压下降,通过测量被测点处的气压,再参考标准大气压模型而算得海拔高度值。
对于惯导系统而言,通常不需对椭球高与海拔高加以细致区分。
实用公式
地球表面附近正常重力随纬度和高度变化的实用计算公式如下:

PSINS中相关代码
在严老师的源码中,也给出了这项的代码
eth.g = eth.g0*(1+5.27094e-3*eth.sl2+2.32718e-5*sl4)-3.086e-6*pos(3); % grs80
地球重力场的球谐函数模型
正常重力场描述的是规则地球假设下产生的重力场,但实际地球并不规则。正常重力场只是实际重力场的一个较好的近似,为了更加细致地刻画实际地球的重力场,需引入球谐函数和重力位等概念,这在高精度惯性导航系统的重力场建模和补偿中十分有用。据统计,与正常重力相比,应用高精度的重力场模型可提升约0.1 n mile/h(1 n mile=1.852 km)的惯性导航精度。
