[数据结构与算法]利用已知矢量在IMU、磁力计的三轴分布获得部分姿态的实例思考与总结

在惯导系统的初始对准，或者AHRS（航姿参考系统）算法中，我们经常通过一些已知方向或者大小的矢量（比如重力、磁力、地球自转角速率），来计算部分姿态参数。

虽然这些做法已经是老生常谈，但是最近看到一个专利，让自己突然意识到这种思路其实有更加广阔的应用，我们不应该把自己的思维局限在这些有限的、已知的应用中。所以写个博客总结一下自己已知的应用实例，巩固一下这种思维方式，希望自己在未来的技术难题中能借鉴这种思路、迸发灵感。

实例一：利用重力在加速度计的三轴分布计算俯仰、横滚

在粗对准中，当载体静止时，通常会根据地球重力在加速度计三轴分布情况，从而计算得到横滚和俯仰。为什么通过加速度只能得到横滚和俯仰，而不能得到航向呢？这个也比较直观，想象一个载体在水平面，转动它的航向，并不能改变重力在加速度计三轴上的分布，但是转动横滚和俯仰却可以。

由于目前加速度计的精度一般都还比较好（多数都能做到$10^{?4}g$），相对来说，1g的重力是一个比较大的测量值，所以一般在静止情况下，这种对准方法精度还是不错的。如果选择北东地为地理系N，前右下为机体系B，则利用加速度计测量值计算粗略横滚、俯仰的方法如下[1]：

PX4的ECL开源代码ekf.cpp中也能找到这种初始水平对准计算方法：

bool Ekf::initialiseTilt()
{
	const float accel_norm = _accel_lpf.getState().norm();
	const float gyro_norm = _gyro_lpf.getState().norm();

	if (accel_norm < 0.8f * CONSTANTS_ONE_G ||
	    accel_norm > 1.2f * CONSTANTS_ONE_G ||
	    gyro_norm > math::radians(15.0f)) {
		return false;
	}

	// get initial roll and pitch estimate from delta velocity vector, assuming vehicle is static
	const Vector3f gravity_in_body = _accel_lpf.getState().normalized();
	const float pitch = asinf(gravity_in_body(0));
	const float roll = atan2f(-gravity_in_body(1), -gravity_in_body(2));

	_state.quat_nominal = Quatf{Eulerf{roll, pitch, 0.0f}};
	_R_to_earth = Dcmf(_state.quat_nominal);

	return true;
}

实例二：利用地球自转角速率在陀螺的三轴分布计算航向

在粗对准中，如果陀螺的精度比较高（可以敏感地球自转角速率约$15°/h$），在静止情况下，可以采用地球自转角速率在IMU的三轴分布来确定航向。

不同的纬度，地球自转角速率不同，且只有北向和地向有值，东向无值。

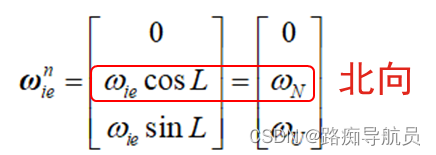
如果已知正确的姿态角，陀螺的测量值经过正确Cbn旋转矩阵从载体系B转到地理系N，由于水平面上只有北向有地球自转角速率分量，因此只有北向的陀螺有值。由实例一可知，在静止情况下通过加速度可以获得俯仰和横滚。在航向角未知的情况下，可以设航向角为0，利用已知的俯仰、横滚将陀螺测量值转到水平面上。

假设航向角为A，那么水平面上陀螺x轴和y轴的分量为：

$w_x=w_{ie}cosL?cosA$
$w_y=?w_{ie}cosL?sinA$

因此，通过如下计算即可航向角A：

$A=?atan2f(w_y,w_x)$

利用这种方法计算出来的航向精度和纬度、陀螺精度都有关系。在博客惯性导航原理(九)-INS的初始对准-初始姿态确定+双矢量定姿中，分析了用这种方法计算航向的精度与维度之间的关系。如果纬度越高，那么在该纬度的北向地球自转角速率分量就越小（天向分量更大），陀螺自身误差的影响就越大，从而导致计算得到的航向误差会越大。

地球自转角速率的量级相对于陀螺精度，其实是一个比较小的量测，因此对陀螺的精度高度要求更高。PX4的ECL中没有这部分的代码，主要原因也可能是无人机所用的IMU一般来说精度偏低，无法通过自对准获得航向信息。

此外，在严恭敏老师的讲义《捷联惯导算法与组合导航原理》中也提到用双矢量定姿法得到初始姿态角。其实本质与实例一、二相同。

实例三：利用地磁在磁力计的三轴分布计算磁航向

利用磁力计获得航向的过程中，通过会利用磁力的分布情况得到磁航向。由于磁力计所测得地磁矢量沿磁感线，如果已知正确的姿态角，磁力计的测量值经过正确Cbn旋转矩阵从载体系B转到地理系N，因为地球磁场的切线在南北方向上，理论上水平方向上只有磁北方向有值。与实例二相同，在航向角未知的情况下，可以设航向角为0，利用已知的俯仰、横滚将磁力计测量值转到水平面上，再通过计算$?atan2f(m_y,m_x)$，即可得到磁航向角。

不过需要注意的是磁北和地理北向之间存在磁偏角，需要根据模型进行修正，才能真正得到航向角。

PX4的ECL开源代码ekf_helper.cpp中的resetMagHeading函数即是用这种方法重置航向角：

// Reset heading and magnetic field states
bool Ekf::resetMagHeading(const Vector3f &mag_init, bool increase_yaw_var, bool update_buffer)
{
	// prevent a reset being performed more than once on the same frame
	if (_imu_sample_delayed.time_us == _flt_mag_align_start_time) {
		return true;
	}

	// calculate the observed yaw angle and yaw variance
	float yaw_new;
	float yaw_new_variance = 0.0f;

	if (_params.mag_fusion_type <= MAG_FUSE_TYPE_3D) {
		// rotate the magnetometer measurements into earth frame using a zero yaw angle
		const Dcmf R_to_earth = updateYawInRotMat(0.f, _R_to_earth);

		// the angle of the projection onto the horizontal gives the yaw angle
		const Vector3f mag_earth_pred = R_to_earth * mag_init;
		yaw_new = -atan2f(mag_earth_pred(1), mag_earth_pred(0)) + getMagDeclination();

		if (increase_yaw_var) {
			yaw_new_variance = sq(fmaxf(_params.mag_heading_noise, 1.0e-2f));
		}

	} else if (_params.mag_fusion_type == MAG_FUSE_TYPE_INDOOR) {
		// we are operating temporarily without knowing the earth frame yaw angle
		return true;

	} else {
		// there is no magnetic yaw observation
		return false;
	}

	// update quaternion states and corresponding covarainces
	resetQuatStateYaw(yaw_new, yaw_new_variance, update_buffer);

	// set the earth magnetic field states using the updated rotation
	_state.mag_I = _R_to_earth * mag_init;

	resetMagCov();

	// record the time for the magnetic field alignment event
	_flt_mag_align_start_time = _imu_sample_delayed.time_us;

	return true;
}

实例四：Trimble专利-计算推土机和推土铲之间的相对航向

在Trimble 2021的专利（参考[3]）中，IMU1装在C-frame上，IMU2装在推土铲上，如下图中所示。

由于C-frame和推土铲半固连，因此他们拥有同样的俯仰角和俯仰角速率，但是横滚和航向可能不同。IMU的横滚、俯仰通常可以通过加速度计得到，两个IMU的相对航向可以通过给他们施加一个同样的、在俯仰方向的角速率得到。这个施加的俯仰角速率，由于两个IMU的姿态不同，因此在两个IMU上有不同的三轴分布。

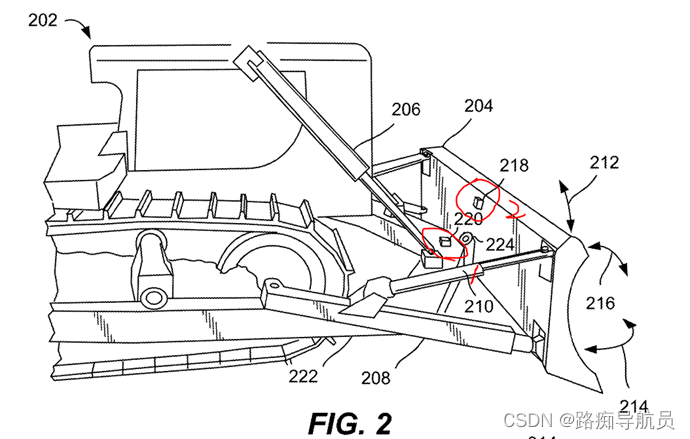
为了求得C-frame和推土铲的相对航向，可以对推土铲进行上下俯仰机动。如果将载体坐标系定义为前右下（XYZ），则此时IMU1的陀螺只有Y轴方向有值，而IMU2由于横滚和航向可能不同，因此陀螺三个轴上可能都有值，但是三轴角速率的矢量和与IMU1一致。

利用加速度计通过实例一中的方法，可以获得每个IMU的横滚和俯仰，因此可以将航向角设置为0，利用各自的横滚、俯仰值将陀螺量测量转到水平面。那么两个陀螺仪在水平方向的矢量和相同，因此可以同以下方式求得相对航向：

整体流程如下：

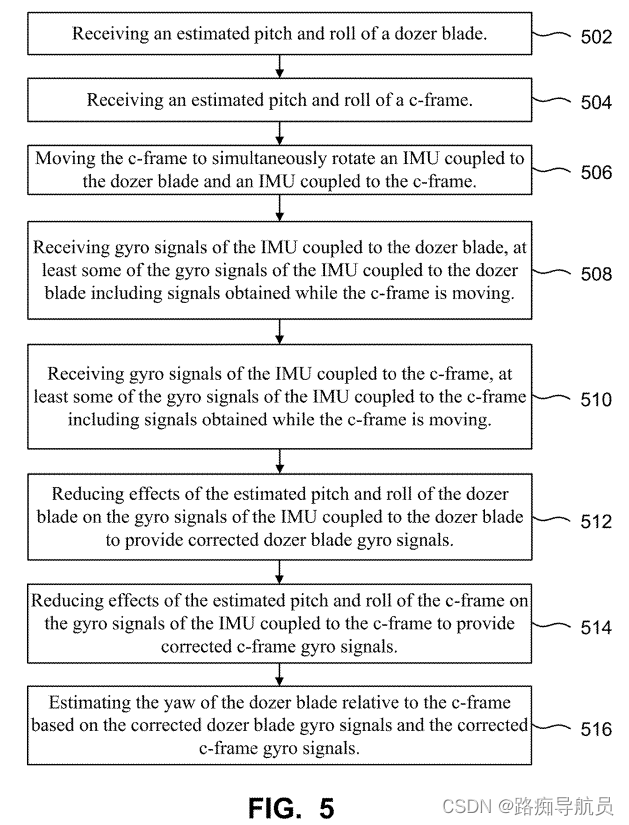
参考资料

[1] 如何利用惯性测量单元（IMU）进行动态姿态计算？
[2] Psins代码解析之粗对准(test_align_methods_compare.m)&精对准
[3] US10968606.pdf
[4] 惯性导航原理(九)-INS的初始对准-初始姿态确定+双矢量定姿

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系