[数据结构与算法]VirtualLab基础实验教程-4.单缝衍射

前言

本篇为大创团队的第四篇集体作品，针对物理光学的基础实验–单缝衍射与矩孔衍射做出了探索和尝试。

一、单缝衍射实验原理简介

1.衍射简介

单缝衍射是光在传播过程中遇到障碍物，光波会绕过障碍物继续传播的一种现象。如果波长与缝、孔或障碍物尺寸相当或者更大时，衍射现象最明显。
菲涅尔衍射：
在光学里,菲涅耳衍射指的是光波在近场区域的衍射,即光源或衍射的图样的屏与衍射孔(障碍物)的距离是有限的。光源和光屏到障碍物的距离均不是很远，并且没有使用透镜。此时光线不是平行光，即波阵面不是平面。
夫琅禾费衍射：
光源和光屏到障碍物的距离都很大，此时入射光为平行光，波面是平面，衍射光也是平行光。这种衍射称为夫琅禾费衍射。在实验室里，我们可以很容易的用透镜使入射球面光波变成平行光，很容易实现夫琅禾费衍射的条件。
显然，菲涅尔衍射是普遍情况，夫琅禾费衍射只是它的特例。

2.半波带分析法

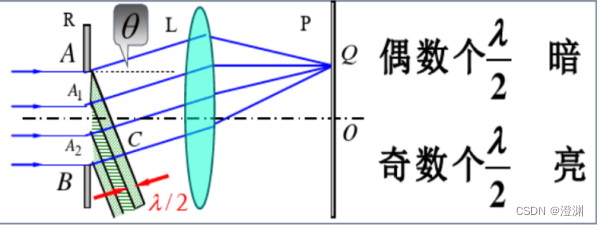
在给定的衍射角$\theta$中，若$BC$刚好截成偶数个半波带，则$Q$点为相消干涉而出现暗纹；若$BC$刚好截成奇数个半波带，余的一个半波带不能被抵消，则点$Q$为相消干长而出现亮纹；若$BC$不为半波长的整数倍，则$Q$点的亮度介于次极大和极小之间，这也说明了每一级条纹都有相应的宽度。
另外，若$\theta$角越大，则$BC$越长，因而半波带数目越多，而缝宽$AB$为常数，因而每个半波带的面积要减少（即每个半波带上携带的光能量减少），于是级数越高，明条纹亮度越低，最后成模糊一片。也因此可以观察到的衍射级次也是有限个的。

3.公式

亮纹条件$bsin\theta =\pm （2k+1）\frac{\lambda }{2}$
暗纹条件$bsin\theta =k\lambda$
中央明纹$?\lambda <bsin\theta <\lambda$，角宽度$2{\theta }_0=2\frac{\lambda }{b}$，线宽度$\Delta x_0=2\frac{\lambda }{b}f$
其他各级明纹的宽度为相邻暗纹间距$\Delta x=\frac{\lambda f}{b}$，可见中央明纹约为其他各级明纹宽度的两倍。

4.影响衍射的因素

缝越窄，衍射越显著，但$b$不能小于$\lambda$($b$小于$\lambda$时，半波带理论不成立。）
缝越宽，衍射越不明显，条纹向中心靠近，逐渐变成直线传播。
$\lambda$越大，衍射现象越明显。
当白光入射时，中央明纹仍为白色，其他各级由紫至红，一般第$2,3$级即开始重叠。
单缝上下移动，根据透镜成像原理衍射图不变。将单缝位置稍稍作上下平移，对衍射条纹不会产生任何影响;将透镜位置稍稍作上下平移，则所有条纹也将随之上下平移,但条纹间距不变。

5.矩孔衍射

$E(x,y)=C{\int }_{?\frac{a}{2}}^{\frac{a}{2}}exp(?i2\pi u{x}_1)d{x}_1{\int }_{?\frac{b}{2}}^{\frac{b}{2}}exp(?i2\pi v{y}_1)d{y}_1$
注：其衍射图样正是其傅里叶变换图样。
$=Cab\frac{sin\alpha }{\alpha }?\frac{sin\beta }{\beta }$
$u=\frac{x}{\lambda f},v=\frac{y}{\lambda f}$
$\alpha =\frac{\pi x}{\lambda f}a,\beta =\frac{\pi y}{\lambda f}b$

6.讨论Y轴条纹分布

$I_y=I_0(\frac{sin\beta }{\beta }{)}^2$
主极大的位置$\beta =0,I_{max}=I_0$
极小值的位置$\beta =n\pi ,n=\pm 1,\pm 2$
即$y=\frac{n\lambda f}{b}$，故中央亮纹宽度$Y=\frac{2\lambda f}{b}$，次级大的位置$\frac{d}{d\beta }\frac{sin\beta }{\beta }=0$
暗纹间隔：$e=\frac{\lambda f}{b}$

二、Virtualab仿真

1.搭建光路

首先在库中找到平面波并拖入面板中：

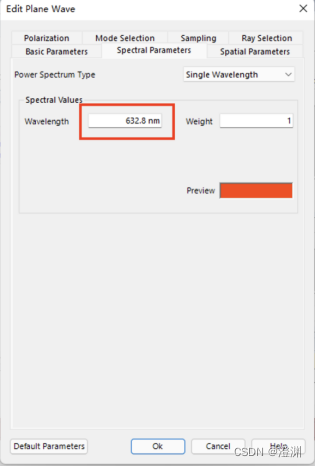
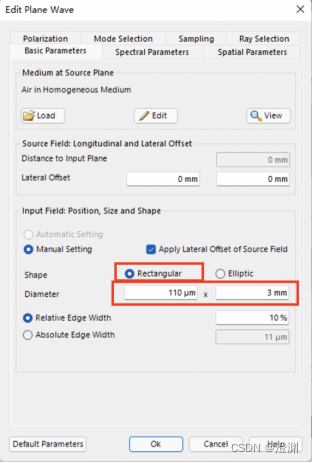
双击设置平面波的属性：
设置波长为632.8nm的红光，并且设置波的形状为矩形，大小为110um×3mm（波源的大小稍大于孔）：
PS：事实上只要比孔大，再大很多也都是可以的


在库中找到Aperture。

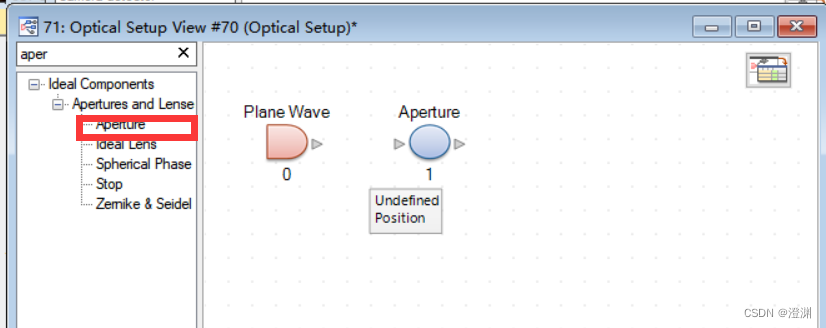
在波源后拖入小孔并设置小孔的参数为矩形孔100um×3mm（由于不是理想的单缝，还是有长和宽的限制，也即一个非常狭长的矩孔）

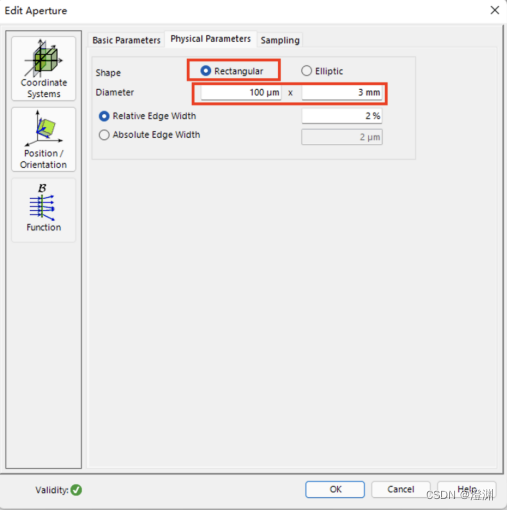
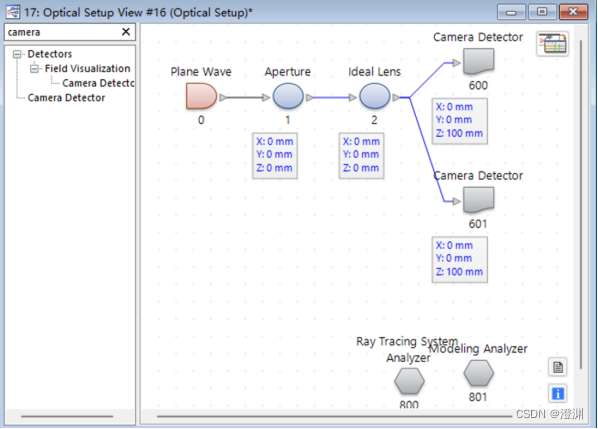
在其后放置一个无限大的理想透镜，焦距为100mm。

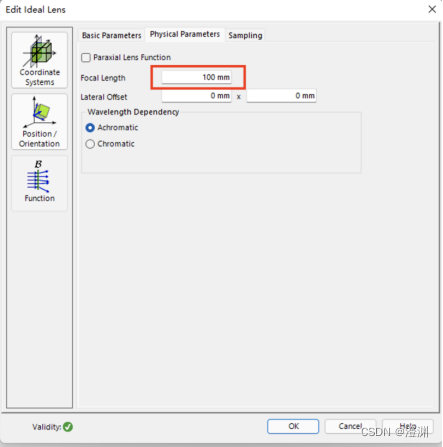
2.探测器的关键之处

在透镜的焦点处放置两个探测器分别形成二维图像和一维图像，两个探测器的距离均设置为100mm（探测器始终在焦平面）

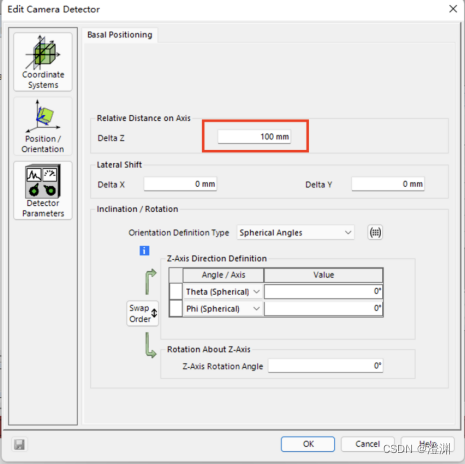
（1）二维探测器的设置：
设置探测窗口大小为20mm×2mm

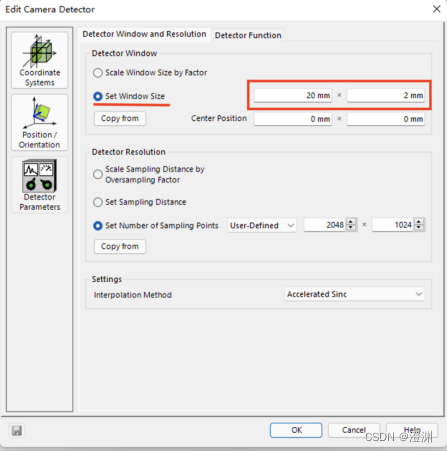
设置采样点的设置改为user defined并且设为2048×1024

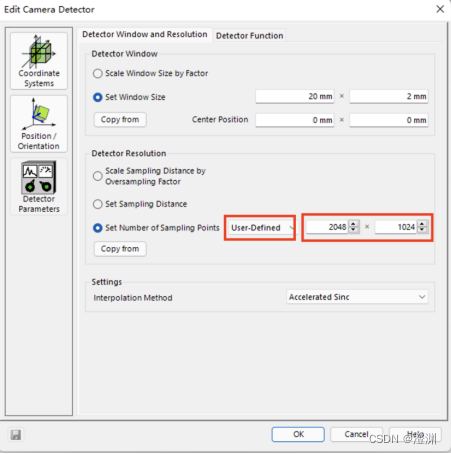
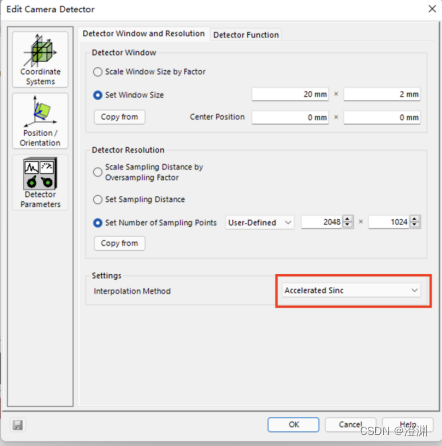
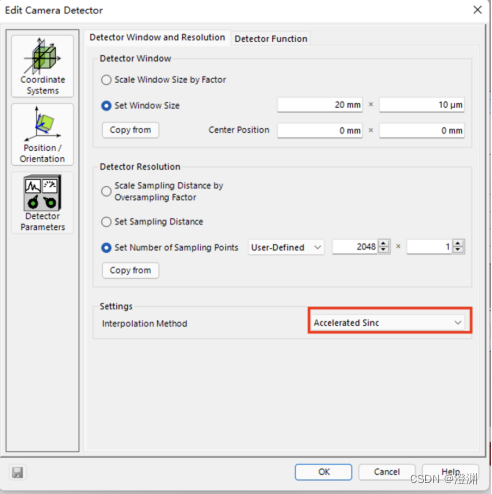
注意：需要将探测器默认的插值方法Cubic 6 Point改为Accelerated Sinc
否则衍射结果只可看到两级。

（2）一维探测器设置：

设置探测器窗口大小为20mm×10um

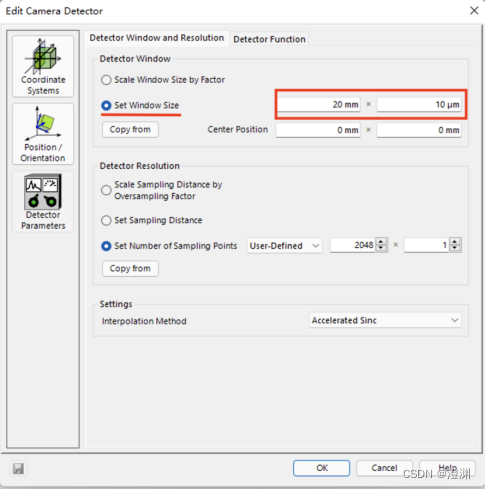
设置采样点的设置改为user defined并且设为2048×1

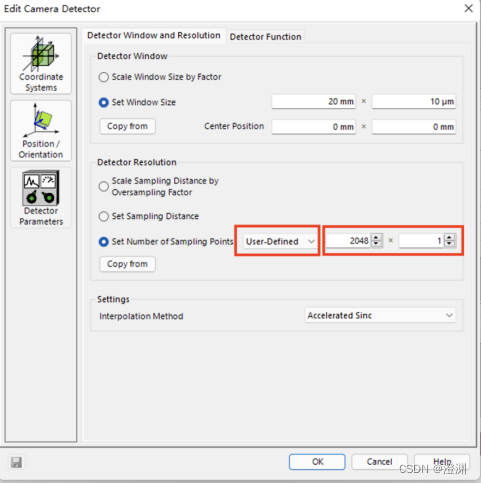
同样需要改变探测器默认的插值方法Cubic 6 Point改为Accelerated Sinc

3.完成效果与经典场追迹

搭建好的光路图为：

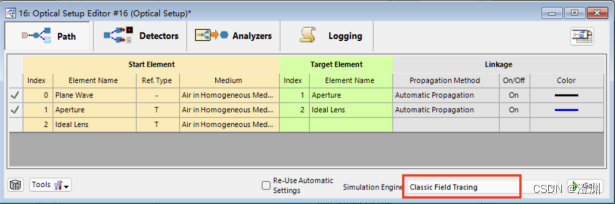
由于所用器件均为理想器件，可使用classic field tracing

得到一维二维的图像：


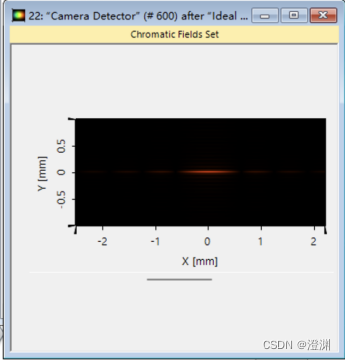
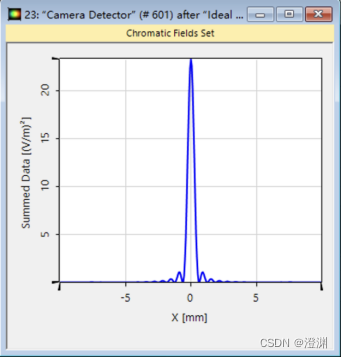
至此基本实验完成。

三、结果展示

接下来，我们对参数进行调整，观察单缝衍射的动态变化情况。

1.改变焦距

首先，将焦距从50mm到1000m变化，此时需要同步变换探测器的距离。


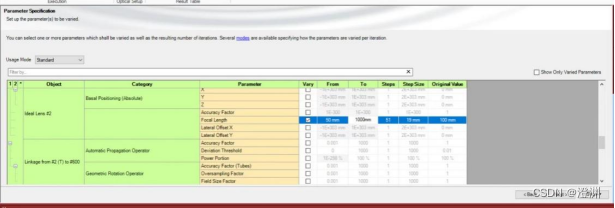
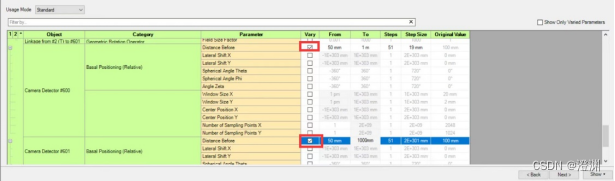
使用parameter run，运行后得到这样的实验结果。

由公式可以得到，当其他条件不变时，焦距增大，中央主极大的宽度增大，即会出现中央主极大展宽，次级亮纹位置外移的现象。

2.改变波长

接着，将波长从400nm到700nm变化。

运行后得到如下的实验结果。

和上面改变焦距时的原理相似，当其他条件不变时，依旧可以由公式推出，当波长增加时，单缝衍射现象类似，都出现中央主极大变宽，次级亮纹位置外移的现象。

3.改变缝宽

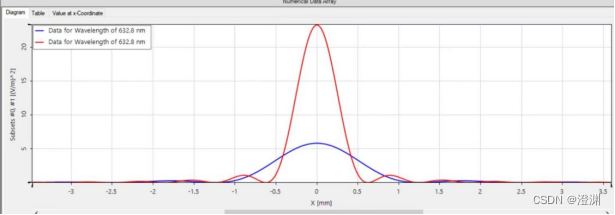
同理，我们用parameter run改变缝宽（40um-115um），运行后，可以获得这样的动态衍射结果。

当其他条件不变时，由公式可以推出，缝宽增加，e减小，即中央主极大宽度变窄，出中央主极大变窄，次级亮纹位置内移的现象。

将50um缝宽（蓝）和100um缝宽（红）的图像合成在一起进行比较，可以发现，红线的中央主极大宽度小于蓝线，符合理论推论。

4.移动单缝位置

把单缝（通光孔径）在空域中横向平移，结果对比图如下：

衍射屏上通光孔径在空域中横向平移，并不影响夫琅禾费衍射的光强振幅分布，只是其相位有一线性变化，接受面上的光强分布不变。

5.移动透镜位置

当透镜在空域中横向平移时，结果图如下，蓝色线为原来的情况，红色线表示平移后图像。

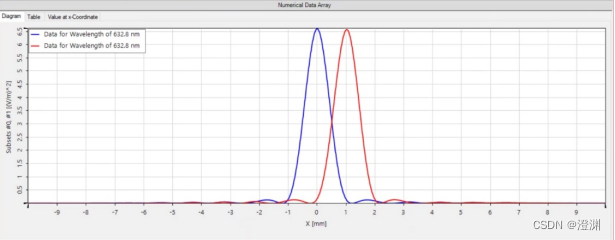
空域中的线性相移引起频谱分布的横向移动，孔径或衍射屏被一束单位振幅的倾斜平面波照射时，夫琅和费光强分布发生横向平移。

6.用矩形光栅构建一个单缝

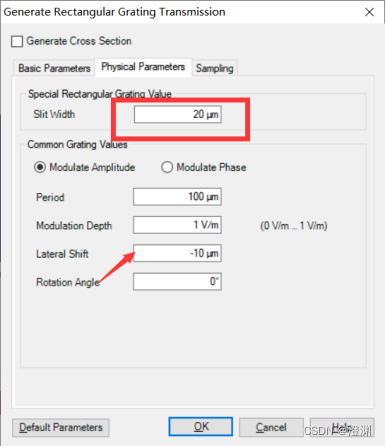
另外，如何构建一个完美的单缝。使用Rectangular Grating.

设置缝宽，此处下方偏移设不设置都不影响最终的条纹位置。

把单缝用这个元件替代,更改完善原先的光路图搭建。

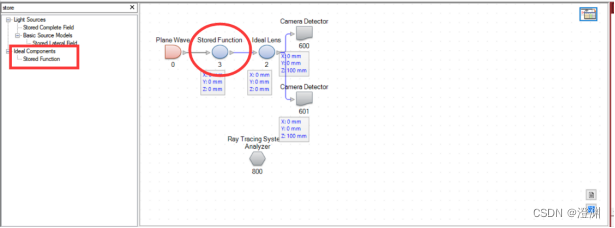
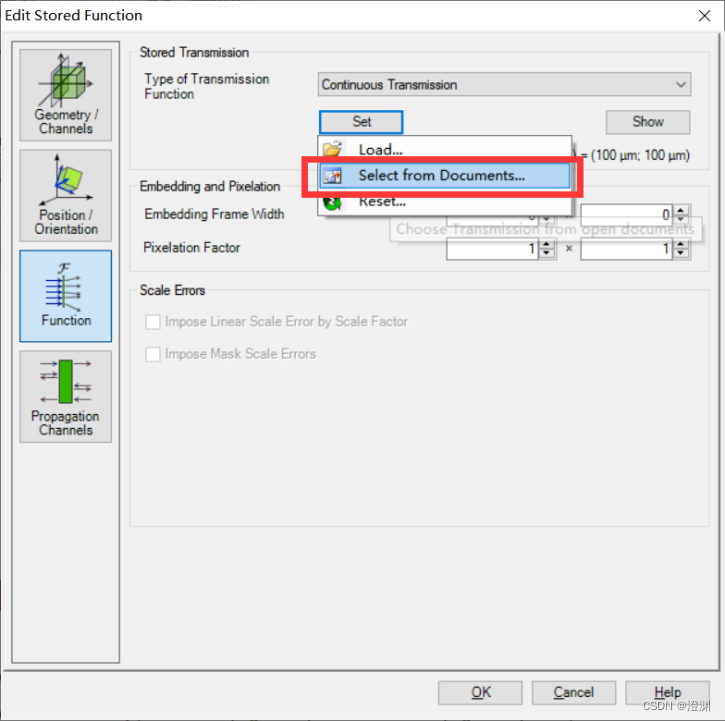
接着，导入刚创建好的透过率函数。

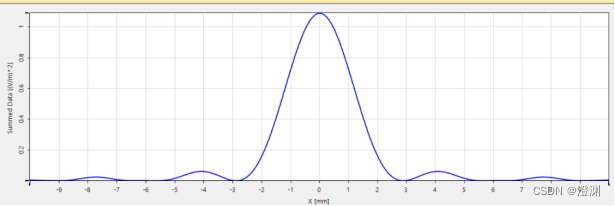
运行后，结果如下，效果较为理想，能很好地观察到中央主极大和次级大的宽度和位置。

7.传统矩孔衍射

若设置成矩孔衍射，单缝参数更改为

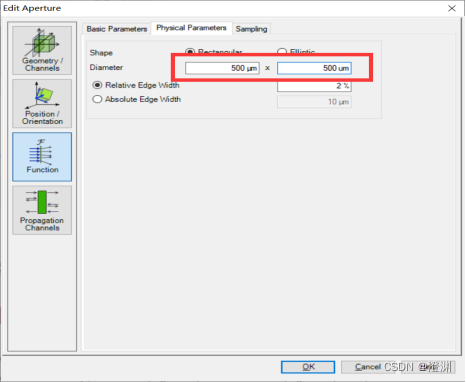
同时，光源参数也要大于单缝。

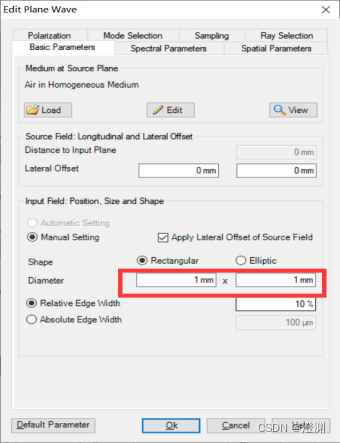
运行后，可以得到这样的实验仿真图像。

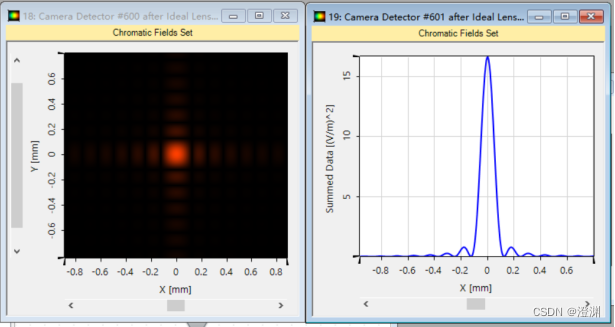
附

本篇由大创团队成员：唐艺恒、扶杨玉、黄一诺、李思潼、明玥共同完成。
本篇采用市面上流通比较广的试用版和7.6.1.18版本进行实验和演示，增强了适用性。
单缝衍射是衍射理论中很重要的实例，此篇为夫琅和费衍射。

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系