[数据结构与算法]数据结构与算法基础知识（三）：常见排序、搜索算法

系列文章

数据结构与算法基础知识（一）：时间复杂度和空间复杂度
数据结构与算法基础知识（二）：常见数据结构
数据结构与算法基础知识（三）：常见排序、搜索算法

前言

本篇介绍一些比较常见的排序算法与搜索算法。

• 排序：把某个乱序的数组变成升序或者降序的数组。
• 搜索：找出数组中某个元素的下标。

冒泡排序

思路：

• 两两比较arr数组中所有相邻元素，如果前一个比后一个大，则交换它们；
• 一轮下来，可以保证最后一个数是最大的；
• 执行arr.length - 1轮，就可以完成排序。

演示：

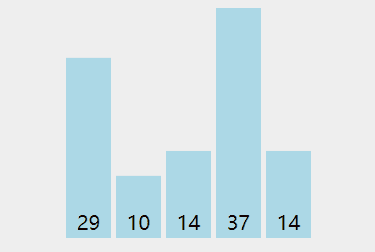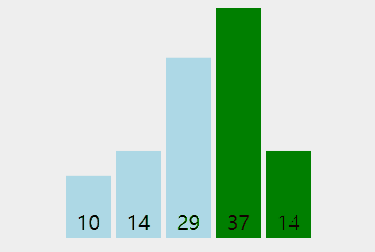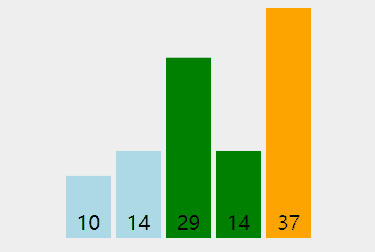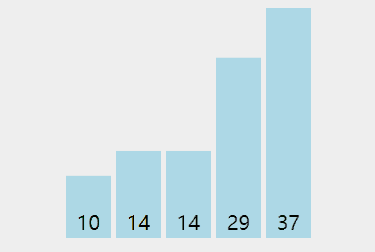
代码：

function swap(arr, i, j) {
    const temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

function bubbleSort(arr) {
    for (let i = 0; i < arr.length - 1; i++) {
        let didSwap = false
        for (let j = 0; j < arr.length - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                swap(arr, j, j + 1)
                didSwap = true
            }
        }
        if (!didSwap) break
    }
}

复杂度：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

选择排序

思路：

• 找到数组中的最小值，与数组第一个元素进行交换；
• 找到数组中第二小的值，与数组第二个元素进行交换；
• 以此类推，执行arr.length - 1轮。

演示：

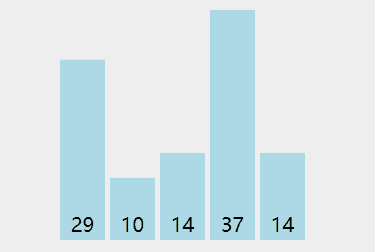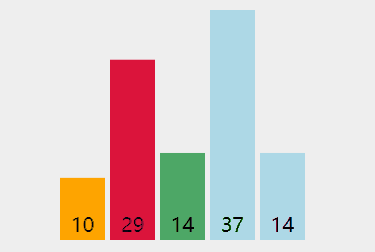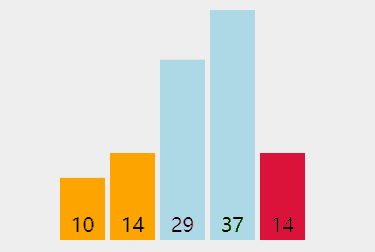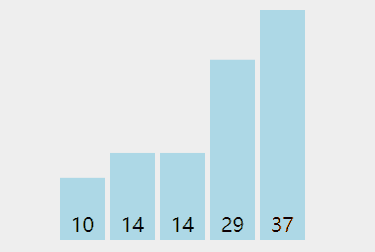
代码：

function swap(arr, i, j) {
    const temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

function selectionSort(arr) {
    for (let i = 0; i < arr.length - 1; i++) {
        let idMin = i
        for (let j = i; j < arr.length; j++) {
            if (arr[j] < arr[idMin]) idMin = j
        }
        if (idMin !== i) swap(arr, i, idMin)
    }
}

复杂度：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

插入排序

思路：

• 数组第二个元素与前面的元素比较，遇到比它大就排它后面。
• 数组第三个元素与前面的元素比较，遇到比它大就排它后面。
• 以此类推，执行arr.length - 1轮。

演示：

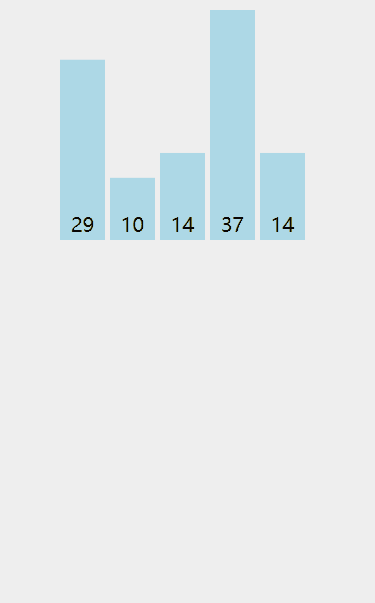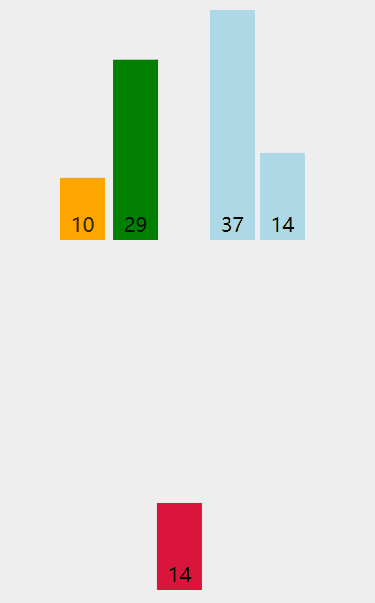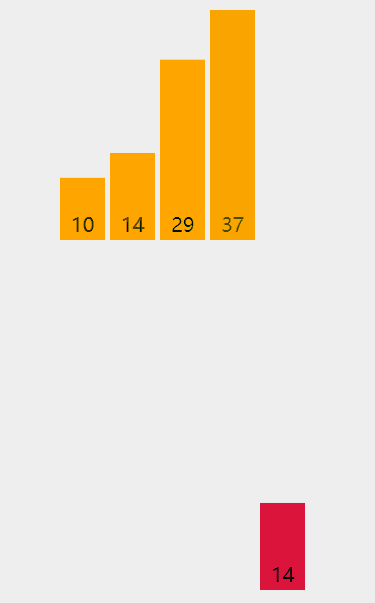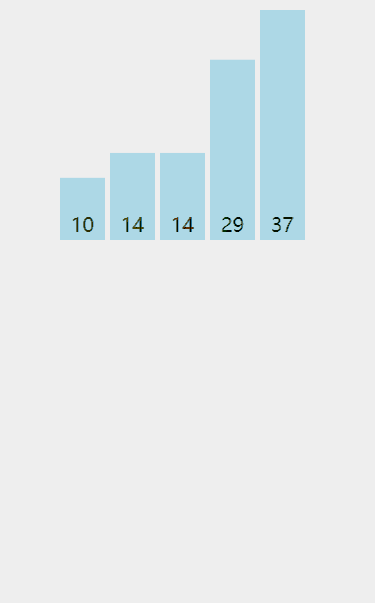
代码：

function insertionSort(arr) {
    for (let i = 1; i < arr.length; i++) {
        const temp = arr[i]
        let j
        for (j = i; j > 0 && arr[j - 1] > temp; j--) {
            arr[j] = arr[j - 1]
        }
        arr[j] = temp
    }
}

复杂度：

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

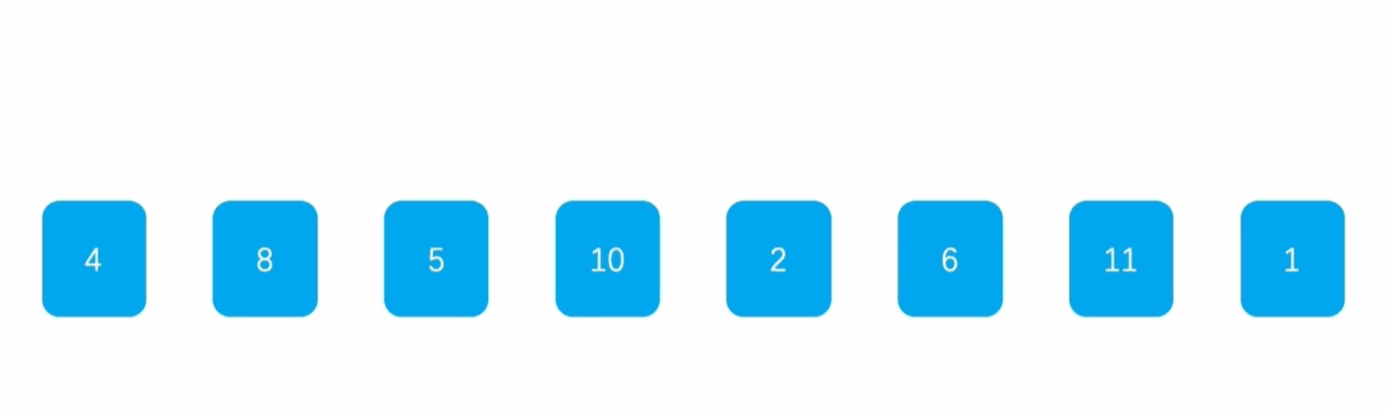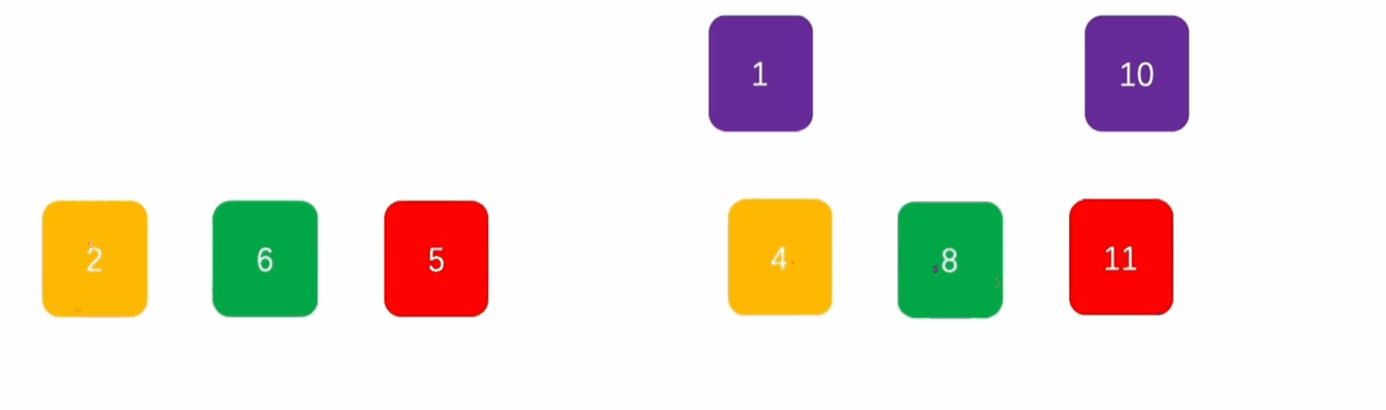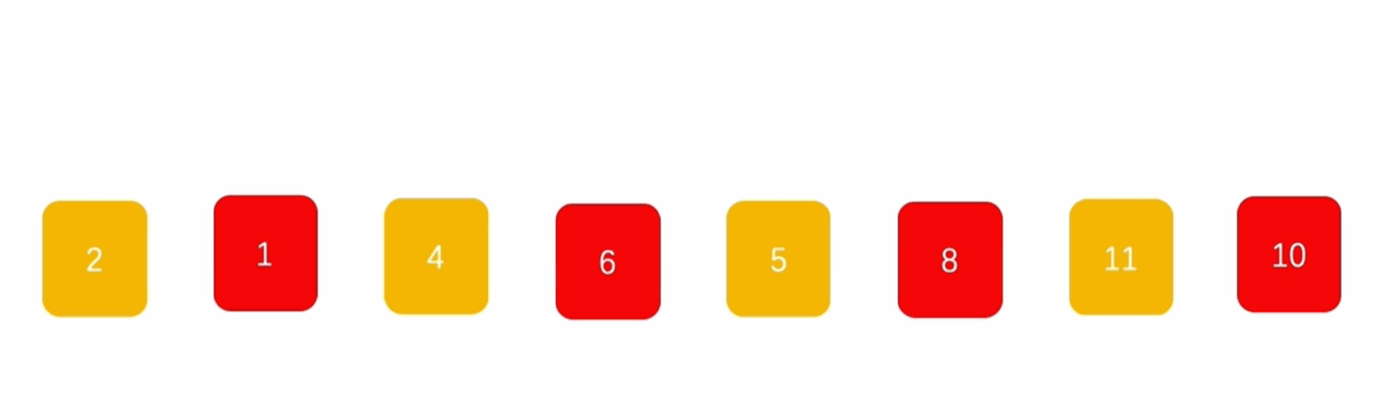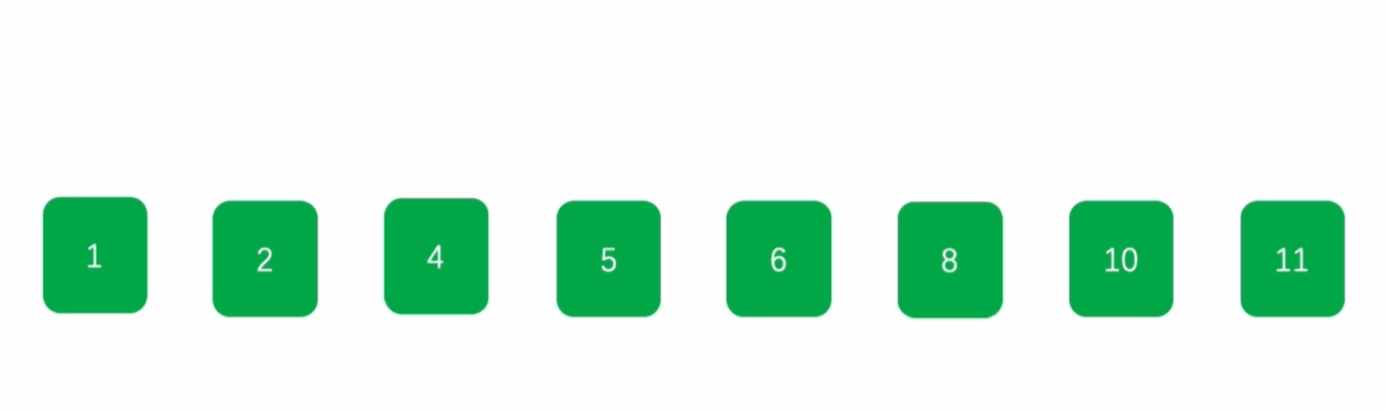
希尔排序

思路：

• 根据数组长度得到间隔大小，按照间隔对数组进行分组，各组内部进行插入排序；
• 缩小间隔大小，按照间隔对数组进行分组，各组内部进行插入排序；
• 以此类推，当间隔缩小为1，对数组整体进行插入排序。

演示：

代码：

function shellSort(arr) {
    let interval = arr.length >> 1
    while (interval >= 1) {
        for (let i = interval; i < arr.length; i++) {
            let temp = arr[i]
            let j
            for (j = i; j - interval >= 0 && arr[j - interval] > temp; j -= interval) {
                arr[j] = arr[j - interval]
            }
            arr[j] = temp
        }
        interval = interval >> 1
    }
}

复杂度：

• 时间复杂度：$O(n^{1.3})$~$O(n^2)$
• 空间复杂度：$O(1)$

归并排序

思路：

• 把数组分为左右两个子数组，再对各个子数组进行同样操作（递归），直到每个子数组只包含一个数组元素；
• 把两个子数组合并为一个有序数组，再对合并后的数组进行同样操作（递归），直到全部子数组合并为一个完整有序数组。

演示：

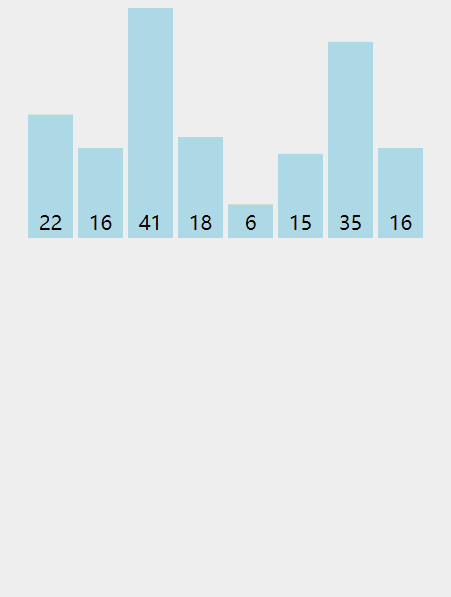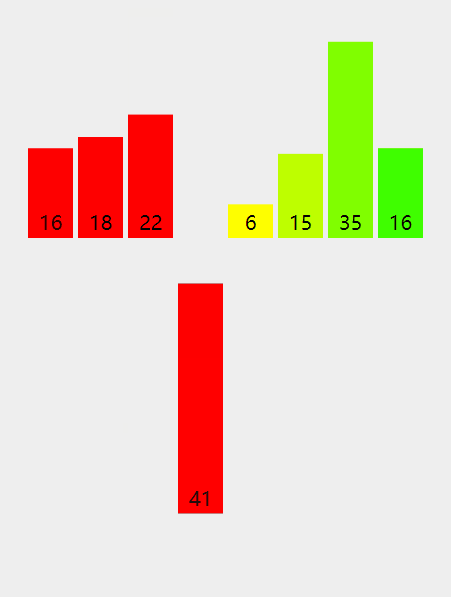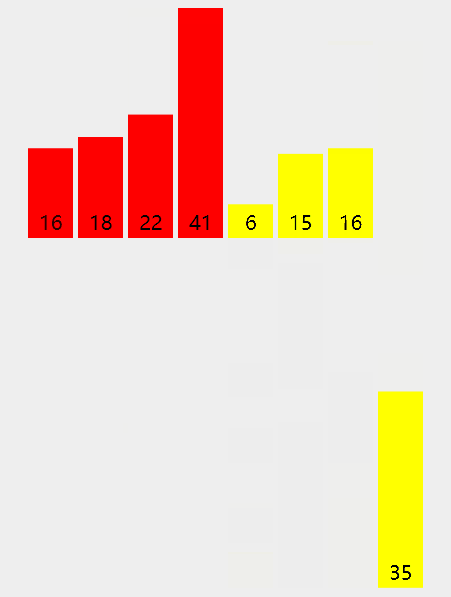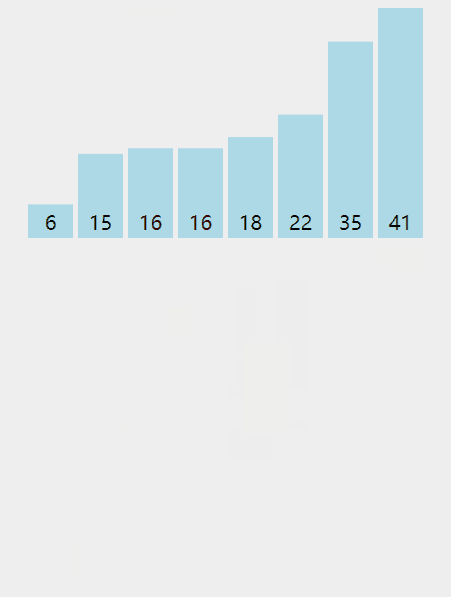
代码：

function mergeSort(arr) {
    if (arr.length === 1) return arr

    const mid = arr.length >> 1
    const left = arr.slice(0, mid)
    const right = arr.slice(mid)

    const resLeft = mergeSort(left)
    const resRight = mergeSort(right)

    const res = []

    while (resLeft.length || resRight.length) {
        if (resLeft.length && resRight.length) {
            res.push(resLeft[0] < resRight[0] ? resLeft.shift() : resRight.shift())
        } else if (resLeft.length) {
            res.push(resLeft.shift())
        } else if (resRight.length) {
            res.push(resRight.shift())
        }
    }

    return res
}
// 未改变原数组

复杂度：

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(n)$

快速排序

思路：

• 定义一个快排函数，先从数组中选取一个支点pivot，快排函数执行完毕后会将数组分为左右两个部分，左半部分所有元素的值小于等于支点pivot，右半部分所有元素的值大于等于支点pivot；
• 对左右两个部分分别调用快排函数（递归）。

演示：

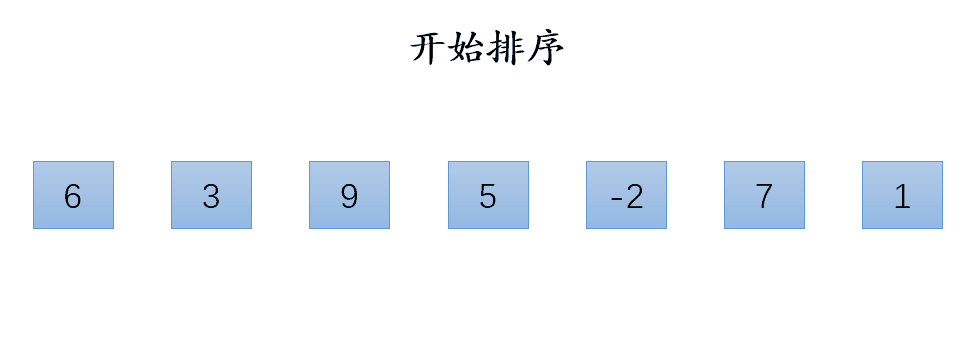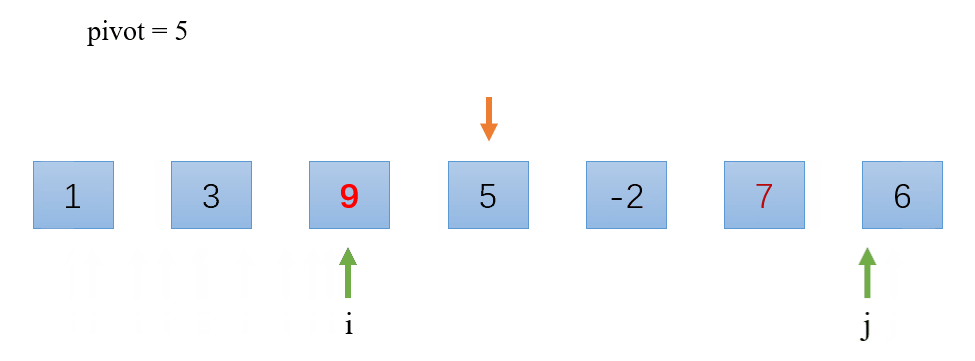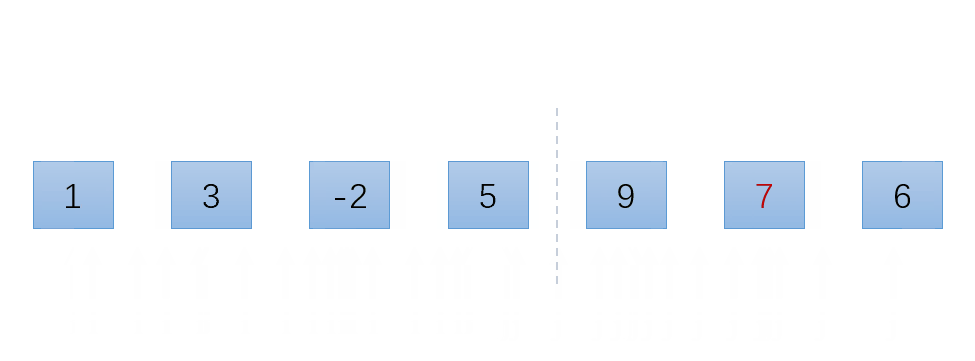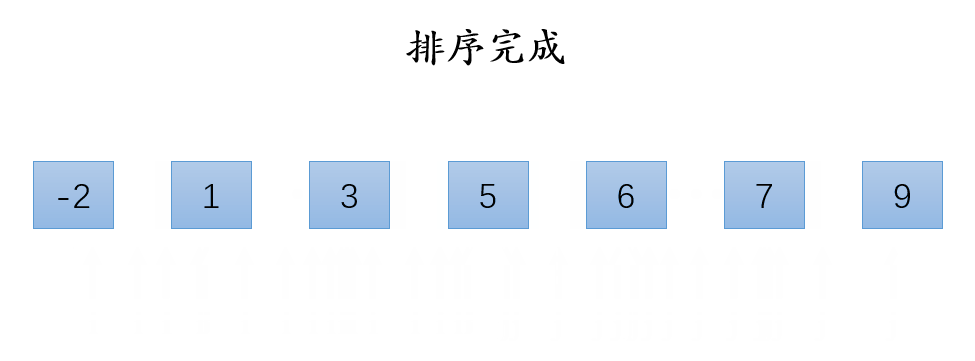
代码：

function quickSort(arr, left, right) {
    if(!arr) return
    left = left === undefined ? 0 : left
    right = right === undefined ? arr.length - 1 : right
    if(!(left < right)) return

    let i = left - 1, j = right + 1
    const pivot = arr[(left + right) >> 1]

    while (i < j) {
        do {i++} while (arr[i] < pivot)
        do {j--} while (arr[j] > pivot)
        if (i < j) { // 如果 i < j，交换 arr[i] 和 arr[j] 的值
            const temp = arr[i]
            arr[i] = arr[j]
            arr[j] = temp
        }
    }

    quickSort(arr, left, j)
    quickSort(arr, j + 1, right)
}

复杂度：

• 时间复杂度：$O(nlogn)$
• 空间复杂度：$O(logn)$

顺序搜索

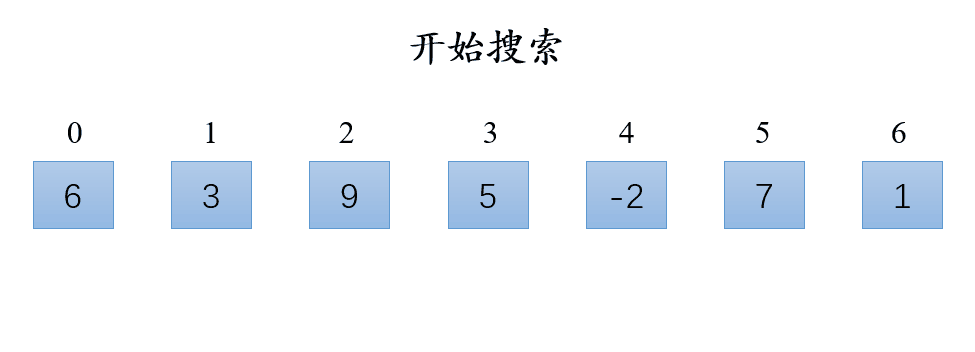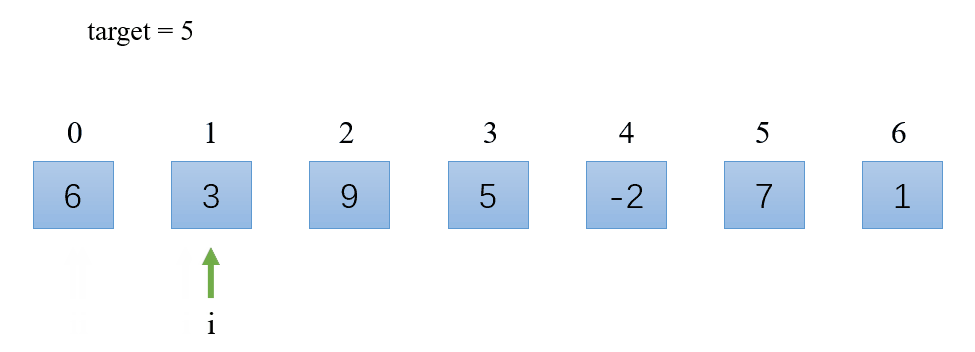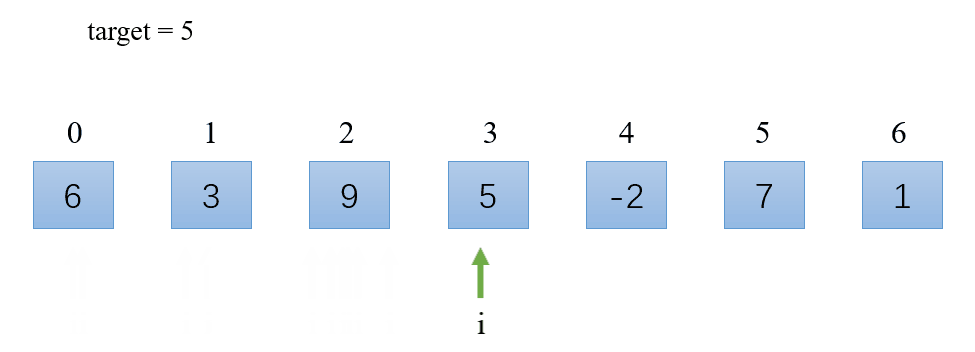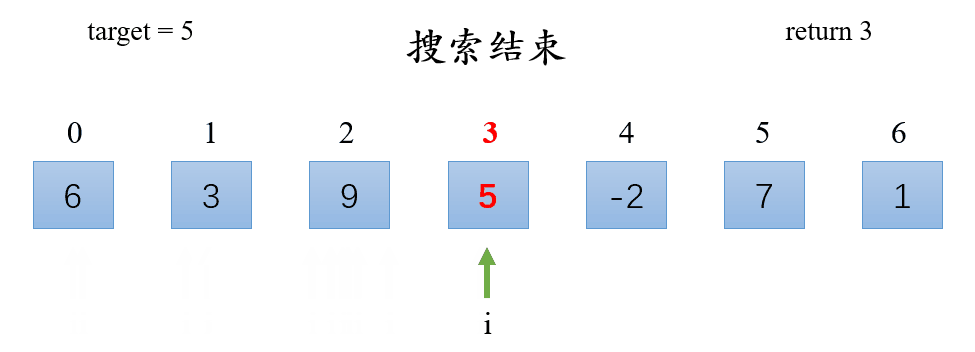
思路：

• 遍历数组；
• 若找到跟目标值相等的元素，则返回它的下标；
• 如果遍历完数组后没有找到跟目标值相等的元素则返回-1。

演示：

代码：

function sequentialSearch(arr, target) {
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === target) return i
    }
    return -1
}

复杂度：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

二分搜索

思路：
适用于已经完成排序的有序数组。

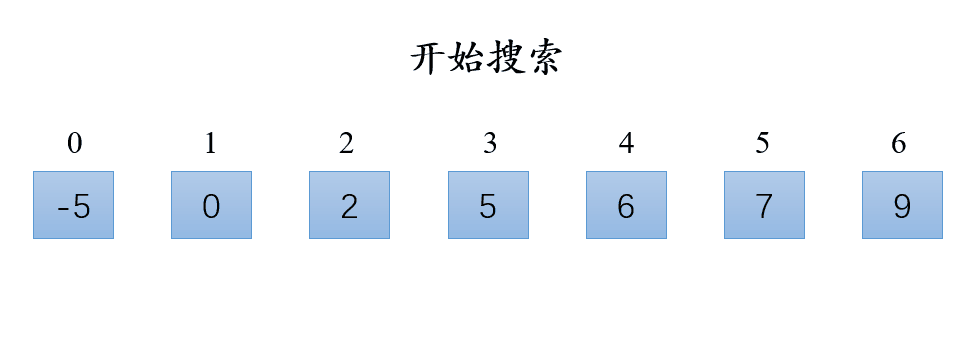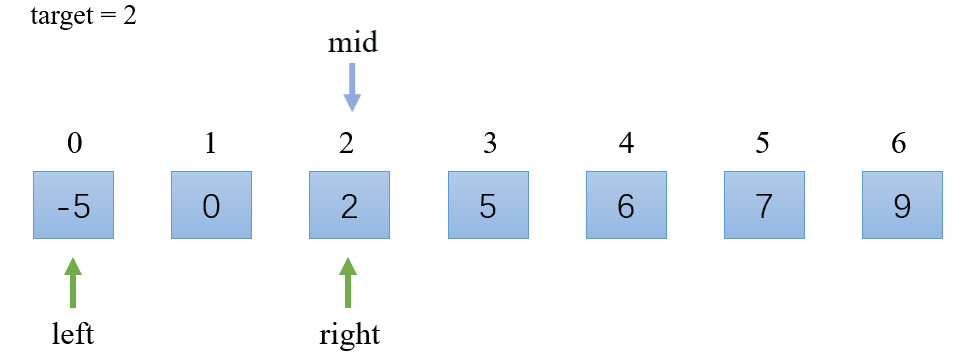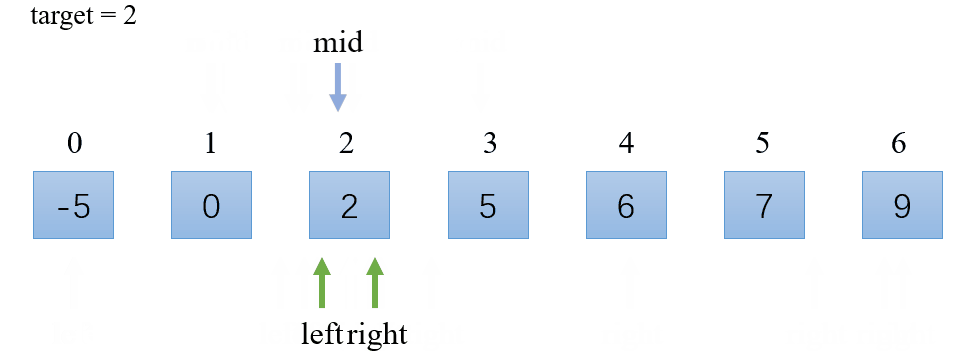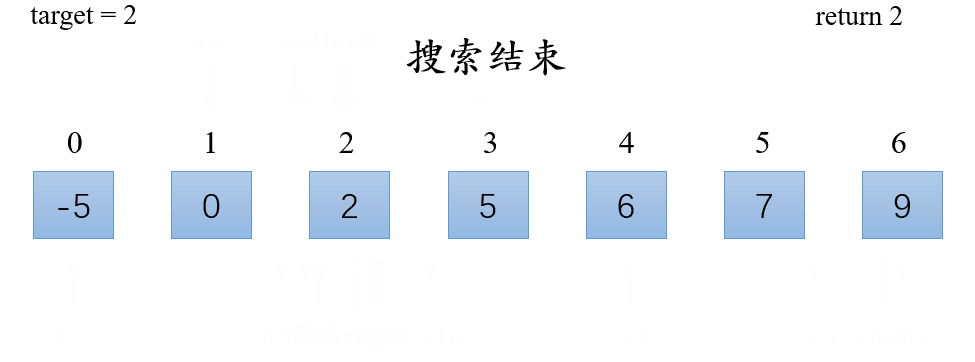
• 二分搜索查找数组中间元素；
• 如果中间元素大于目标值，则对中间元素的左半部分进行二分搜索，否则对中间元素的右半部分进行二分搜索。

演示：

代码：

function binarySearch(arr, target) {
    let l = 0, r = arr.length - 1
    while (l <= r) {
        const m = (l + r) >> 1
        if (arr[m] < target) l = m + 1
        else if (arr[m] > target) r = m - 1
        else return m
    }
    return -1
}

复杂度：

• 时间复杂度：$O(logn)$
• 空间复杂度：$O(1)$

至此，常见的排序算法与搜索算法就介绍完了。创作不易，希望多多支持~~

如有疏漏之处欢迎评论区留言指正~~

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系