[数据结构与算法]LeetCode 31下一个排列、LeetCode 64最小路径和、LeetCode 62不同路径、LeetCode 78子集、LeetCode 33搜索旋转排序数组（修改二分法）

Top1：LeetCode 31下一个排列

题目描述：
以数字序列 [1,2,3][1,2,3] 为例，其排列按照字典序依次为：

[1,2,3]\ [1,3,2]\ [2,1,3]\ [2,3,1]\ [3,1,2]\ [3,2,1]
[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]

这样，排列 [2,3,1][2,3,1] 的下一个排列即为 [3,1,2][3,1,2]。特别的，最大的排列 [3,2,1][3,2,1] 的下一个排列为最小的排列 [1,2,3][1,2,3]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ，找出 nums 的下一个排列。
必须 原地 修改，只允许使用额外常数空间。
示例 1：
输入：nums = [1,2,3]
输出：[1,3,2]

示例 2：
输入：nums = [3,2,1]
输出：[1,2,3]

示例 3：
输入：nums = [1,1,5]
输出：[1,5,1]

一、注意到下一个排列总是比当前排列要大，除非该排列已经是最大的排列。若要满足需要变大的幅度尽可能小，需要从右往左找到一个左边的【较小数】和从右往左找右边的【较大数】，之后将较大数右边的数使用刷给你指针反转区间【其实也是按照升序重新排列】

以排列 [4,5,2,6,3,1][4,5,2,6,3,1] 为例：

• 我们能找到的符合条件的一对「较小数」与「较大数」的组合为 22 与 33，满足「较小数」尽量靠右，而「较大数」尽可能小。
• 当我们完成交换后排列变为 [4,5,3,6,2,1][4,5,3,6,2,1]，此时我们可以重排「较小数」右边的序列，序列变为 [4,5,3,1,2,6][4,5,3,1,2,6]。

可通过完整代码：

public void nextPermutation(int[] nums) {
    int i = nums.length - 2;
    while (i >= 0 && nums[i] >= nums[i + 1]) i--;   // 找到为【较小数】的i，一定要>=不能>，因为要找到较小数nums[i] < nums[i+1]
    if (i >= 0) {   // 如果已经是最大的了，i=-1，此时不满足这个；将会执行最后的reverse
        int j = nums.length - 1;
        while (j >= 0 && nums[i] >= nums[j]) j--;   // 找到为【较大数】的j，一定要有=，因为较大的数一定满足nums[j] > nums[i]
        swap(nums, i, j);   // 交换
    }
    reverse(nums, i + 1);   // 反转较小数的后面
}

private void reverse(int[] nums, int startIndex) {
    int left = startIndex, right = nums.length - 1;   // 从两头开始交换（偶数正好满足，奇数中间的那个不用交换）
    while (left < right) {
        swap(nums, left, right);
        left ++;
        right--;
    }
}

private void swap(int[] nums, int i, int j) {
    int tem = nums[i];
    nums[i] = nums[j];
    nums[j] = tem;
}

Top2：LeetCode 64最小路径和（动态规划）

题目描述：
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。
示例 1：

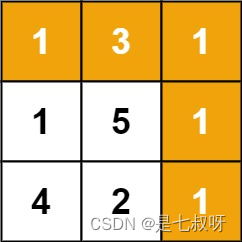
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12

一、【动态规划构造最小路径和的数组，dp[i][j]表示从左上角出发到位置[i][j]的最小路径和】

二、对于在第一列和第一行上的元素直接初始化dp[0][0]后初始化完，不在第一行和第一列的元素使用两个for循环从1到<length按行填，状态转移方程如下：

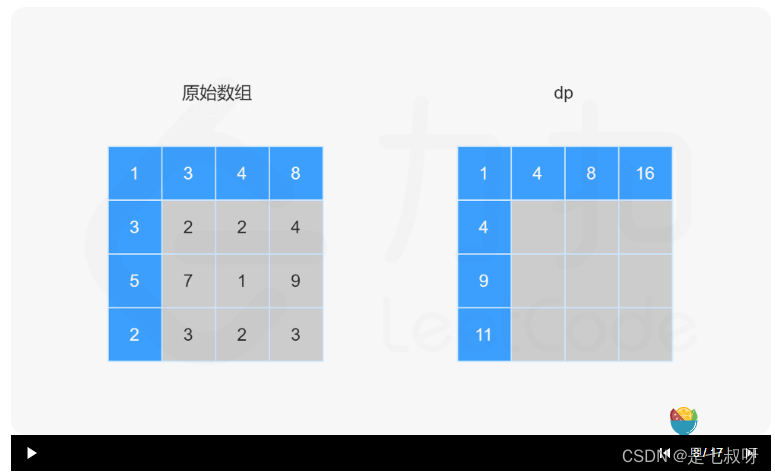
可通过完整代码：

public int minPathSum(int[][] grid) {
    if (grid == null || grid.length == 0 || grid[0].length == 0) {
        return 0;
    }
    int rows = grid.length, cols = grid[0].length;
    int[][] dp = new int[rows][cols];
    dp[0][0] = grid[0][0];   // 初始化左上角第一个元素
    for (int i = 1; i < rows; i++) {   // 填dp矩阵的第一列，从下标1开始
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    }
    for (int j = 1; j < cols; j++) {   // 填dp矩阵的第一行，从下标1开始
        dp[0][j] = dp[0][j - 1] + grid[0][j];
    }
    for (int i = 1; i < rows; i++) {   // 一行一行的填剩余的地方
        for (int j = 1; j < cols; j++) {
            dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        }
    }
    return dp[rows - 1][cols - 1];
}

Top3：LeetCode 62不同路径

题目描述：
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？
示例1：

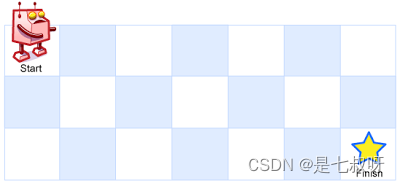
输入：m = 3, n = 7
输出：28

示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：
输入：m = 7, n = 3
输出：28

示例 4：
输入：m = 3, n = 3
输出：6

一、动态规划：因为机器人每次都只能往下or往右，所以第一行和第一列都初始化为1【反证—>多一个下和多一个右都回不去上一行和前一列】，其他的i j=i-1（从上一行往下）+j-1（从前一列往右）【如果都是1，则=1+1=2，就相当于有两条不同路径】

• 时间复杂度O(mn)：两个for循环m * n
• 空间复杂度O(mn)：新建了dp数组来存储不同路径数组的各个数量

可通过完整代码：

public int uniquePaths(int m, int n) {
    int[][] dp = new int[m][n];
    for (int i = 0; i < m; i++) {   // 按行i++填满第一列
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++) {   // 按列j++填满第一行
        dp[0][j] = 1;
    }
    for (int i = 1; i < m; i++) {   // 按i++开始逐列填dp次数矩阵
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];   // 除了第一行和第一列的[i][j]位置有可能从i-1下移，或者j-1右移动【因为机器人每次只能右移或下移】
        }
    }
    return dp[m - 1][n - 1];
}

方法II 组合数学方法：

从左上角到右下角的过程中，我们需要移动 m+n-2 次，其中有 m-1 次向下移动，n-1 次向右移动。因此路径的总数，就等于从 m+n-2 次移动中选择 m-1 次向下移动的方案数【因为每一种组合都可以将n-1次向右移动匹配到】，即组合数：

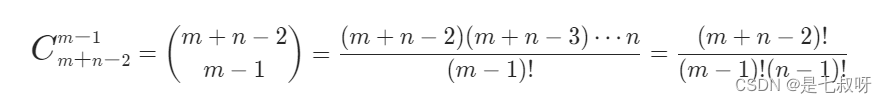
消去分母(n-1)!：

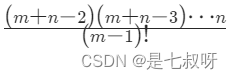
递推

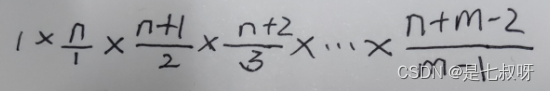
我们直接计算出这个组合数即可得到不同路径数。

• 时间复杂度O(m)
• 空间复杂度O(1)

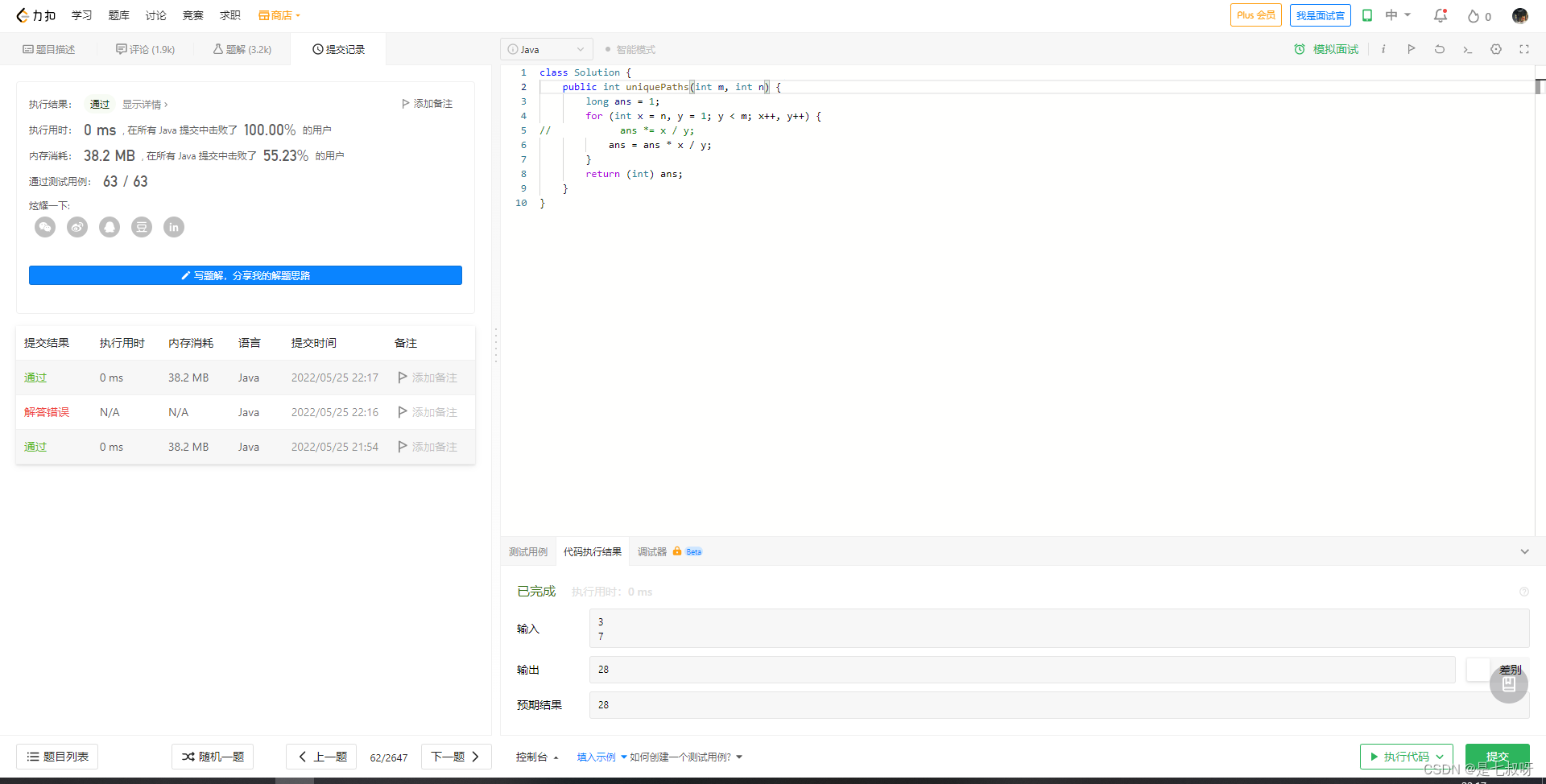
将long类型转变为int，且for循环终止条件：因为每一回合x y都会增加，所以可以写一个终止条件y<m

return (int) ans;

for (int x = n, y = 1; y < m; x++, y++){}

！！！Division result is truncated to integer警告?

猜测此处是因为使用 *= 符号之后，先计算右边int/int了，所以会报除法结果被切断为integer，尽量不同类型的时候不使用 *= 这种符号【使用将会造成奇怪的错误】

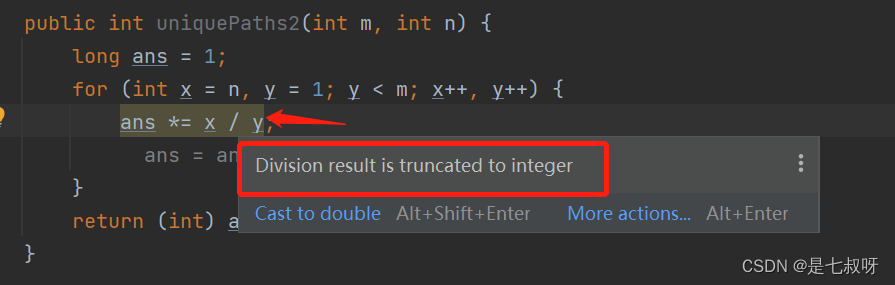
可通过完整代码

public int uniquePaths2(int m, int n) {
    long ans = 1;
    for (int x = n, y = 1; y < m; x++, y++) {
//            ans *= x / y;
        ans = ans * x / y;
    }
    return (int) ans;
}

Top4：LeetCode 78子集（数组中数据互不相同）

题目描述：
给你一个整数数组 nums ，数组中的元素$互不相同$ 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：
输入：nums = [0]
输出：[[],[0]]

一、使用dfs，其中为选择当前位置然后index+1继续下一次，和不选择当前位置remove（sub.size()-1），继续dfs；当index==n-1的时候添加答案进去，return

看下图递归树就可知，要按照代码顺序从右往左输出，所以remove(sub.size()-1)

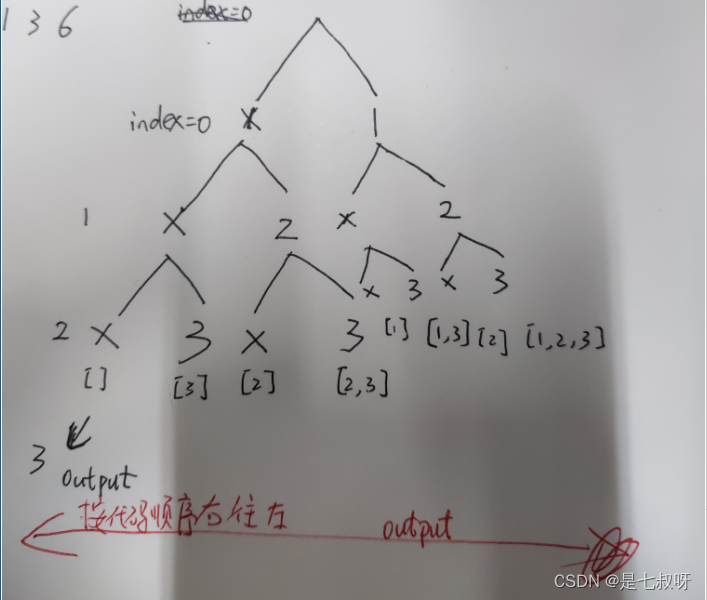
可通过完整代码：

List<List<Integer>> ans = new ArrayList<>();
List<Integer> sub = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
    dfs(0, nums);
    return ans;
}

private void dfs(int index, int[] nums) {
    if (index == nums.length) {   // 当其执行完sub.add()后进入dfs就会输出
        ans.add(new ArrayList<>(sub));
        return;
    }
    sub.add(nums[index]);
    dfs(index + 1, nums);
    sub.remove(sub.size() - 1);   // remove掉sub.size() - 1更保险一些，移除的是前面行添加的nums[index]
    dfs(index + 1, nums);
}

Top4：LeetCode 33搜索旋转排序数组（二分法）

题目描述：
整数数组 nums 按升序排列，数组中的值$互不相同$ 。
在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。
示例 1：
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：
输入：nums = [1], target = 0
输出：-1

一、$对于有序数组，可以使用二分查找的方法查找元素$。所以可以分为左有序（下标l到mid）和右有序（下标mid+1到r）缩小区间

二、我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。先判断==，如果左边有序（下标mid和0比较>=），则判断target是否在有序区间：左>= 右<；如果else则右边有序-即下标mid+1到r有序，继续进行判断是否在区间。

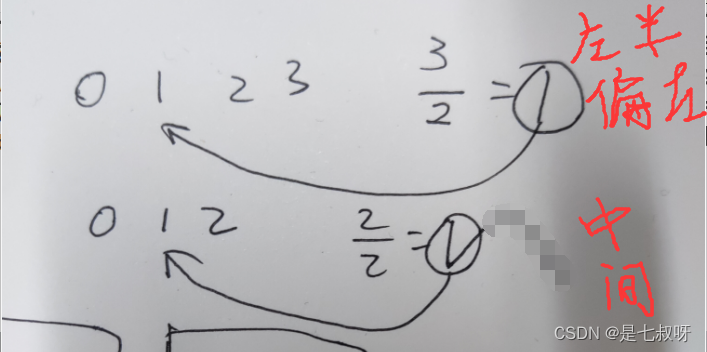
注意，(l + r) / 2：

• 奇数长得到中间元素下标
• 偶数长得到左半边最后一个元素的下标
  

可通过完整代码：

public int search(int[] nums, int target) {
    if (nums.length == 0) return -1;
    if (nums.length == 1) return nums[0] == target ? 0 : -1;
    int l = 0, r = nums.length - 1;
    while (l <= r) {   // 当为单个元素的时候，l=r=0
        int mid = (l + r) / 2;
        if (nums[mid] == target) return mid;   // 已经判断过nums[mid]是否等于target了，所以后续可以直接=mid+-1
        if (nums[mid] >= nums[0]) {   // 说明l到mid为有序，使用nums[0]0判断   // 此处应该为>=，因为当nums=[1,3],target=1的时候，这个if>不满足进入else中mid-r，所以会有r=mid-1最后返回-1了
            if (target >= nums[l] && target < nums[mid]) {   // 因为移动r，所以左边可以相等   // target在左有序
                r = mid - 1;
            } else {   // target不在左有序
                l = mid + 1;   // 因为前面已经判断过nums[mid]==target了，所以这里不用=mid可以直接=mid+1
            }
        } else {   // 当l到mid无序时，说明下标mid+1到右边有序
            if (target > nums[mid] && target <= nums[r]) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
    }
    return -1;   // 都没找到就返回-1
}

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系