目录
1.优先级队列和堆的概念
2.优先级队列的实现
1.优先级队列和堆的概念
1.1.什么是优先级队列??
我们都学过队列,队列是一种先进先出的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,这就是优先级队列。比如有时候我们在打游戏的时候,别人打电话给你,那么系统一定是先处理打进来的电话。
1.2.什么是堆??
简言之,堆其实就是一棵完全二叉树,它的底层是一个数组,数组中存储这棵完全二叉树层序遍历的结果,按种类分,它又分为大根堆和小根堆,请看下图:
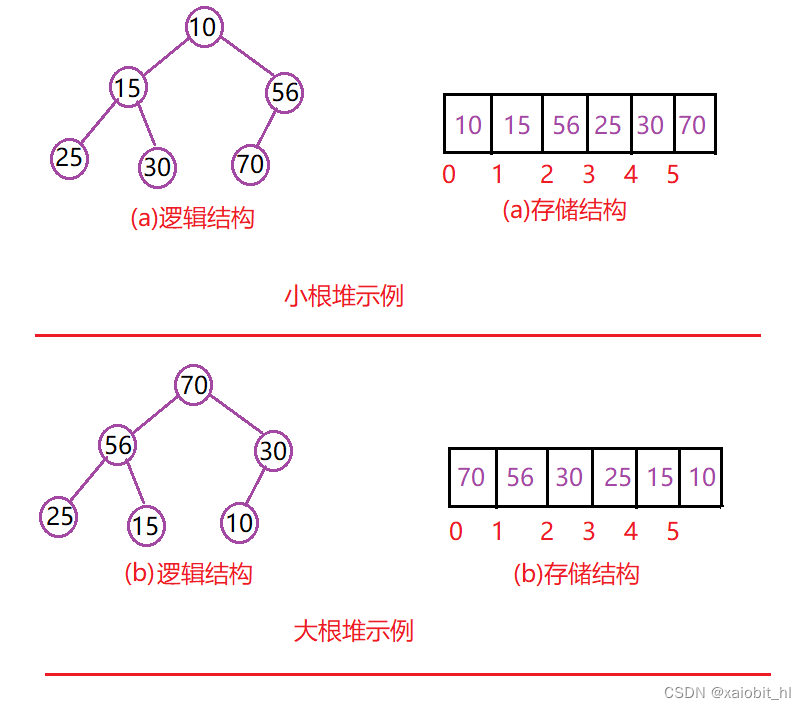
- 性质:
1.堆中的某个结点的值总是不大于或不于其父节点的值;
2.堆总是一棵完全二叉树;
? 所以完全二叉树的性质就可以拿来用:
- 如果 i 为0,则 i 表示的结点为根节点,否则 i 结点的双亲结点为(i -?1)/ 2;
- 如果 2 * i + 1 小于结点个数,则节点 i 的左孩子下标为 2 * i + 1,否则没有左孩子;
- 如果 2 * i + 2 小于结点个数,则节点 i 的左孩子下标为 2 * i + 2,否则没有右孩子。
注意:堆是一棵完全二叉树,它有着层序遍历的规则,所以采用顺序存储的方式来提高效率,而非完全二叉树是不适合使用顺序存储的方式来进行存储的,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。

2.优先级队列的实现
2.1创建大根堆
public class TestHeap {
public int elem[];
public int usedSize;
public static int DEFAULT_SIZE = 10;
public TestHeap() {
this.elem = new int[DEFAULT_SIZE];
}
public int[] createHeap(int[] array) {
//准备数据
for (int i = 0; i < array.length; i++) {
this.elem[i] = array[i];
this.usedSize++;
}
//创建大根堆
for (int p = (this.usedSize - 1 - 1) / 2; p >= 0 ; p--) {
//向下调整
shiftDown(p, this.usedSize);
}
return this.elem;
}
private void shiftDown(int parent, int len) {
//左孩子
int child = 2 * parent + 1;
//每一次调整的结束条件 --> child < len
while(child < len) {
//拿到左右孩子的最大值
if(child + 1 < len && this.elem[child] < this.elem[child + 1]) {
child++;
}
if(this.elem[child] > this.elem[parent]){
swap(parent, child);
//继续判断它子树是否调整
parent = child;
child = 2 * parent + 1;
} else {
//无需调整
break;
}
}
}
private void swap(int parent, int child) {
int tmp = this.elem[parent];
this.elem[parent] = this.elem[child];
this.elem[child] = tmp;
}
}
- 思路

- ?时间复杂度
?1.向下调整的时间复杂度:
最坏情况就是调整完 0 这棵树,那么调整的次数就是完全二叉树的高度,此时时间复杂度为 O(log2^n);
2.建大根堆的时间复杂度:
分析建堆的时间复杂度,我们需要从它的思想层面去分析,不能果断的断定:
每次调整的时间为 O(log2^n),然后调整 n 次,所以时间复杂度为 n * (log2^n),这是错误的!
?假设这棵完全二叉树是一棵满二叉树,树的高度为 n ,那么我们只需要调整第 n 层以上的树(调整 1 -? n - 1层):
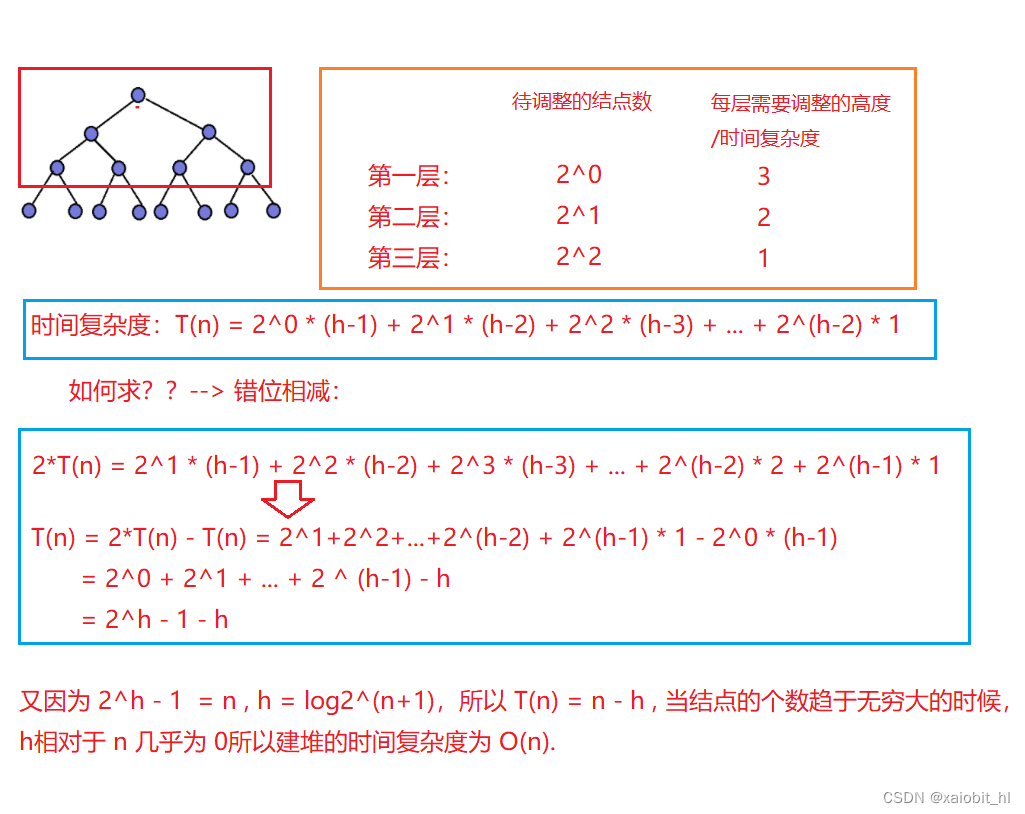
?2.2插入数据
public void offerHeap(int val) {
if(isFull()) {
this.elem = Arrays.copyOf(this.elem, 2*this.elem.length);
}
//1.放在最后一个位置
this.elem[this.usedSize] = val;
//2.进行向上调整
shiftUp(usedSize);
//3.有效数据+1
this.usedSize++;
}
private void shiftUp(int child) {
//父节点
int parent = (child - 1) / 2;
while(child > 0) {
if(this.elem[child] > this.elem[parent]) {
swap(child,parent);
//向上调整
child = parent;
parent = (child - 1) / 2;
} else {
break;
}
}
}
private boolean isFull() {
return this.usedSize == this.elem.length;
}- 思路
1.将待插入的数据放在 usedSize 位置
2.从usedSize下标的数据向上调整
?2.3删除数据
public int pollHeap() {
if(isEmpty()) {
throw new MyHeapIsEmptyException("优先级队列为空!");
}
int tmp = this.elem[0];
//将最后一个数据与堆顶数据进行交换
swap(usedSize-1,0);
this.usedSize--;
//向下调整
shiftDown(0, this.usedSize);
return tmp;
}
private boolean isEmpty() {
return this.usedSize == 0;
}
- 思路
1.将最后一个数据与堆顶数据进行交换
3.将堆中有效数据个数减少一个
2.然后再进行向下调整
2.4获取堆顶元素
public int peekHeap() {
if(isEmpty()) {
throw new MyHeapIsEmptyException("优先级队列为空!");
}
return this.elem[0];
}谢谢观看!!!
