
什么是幻方?
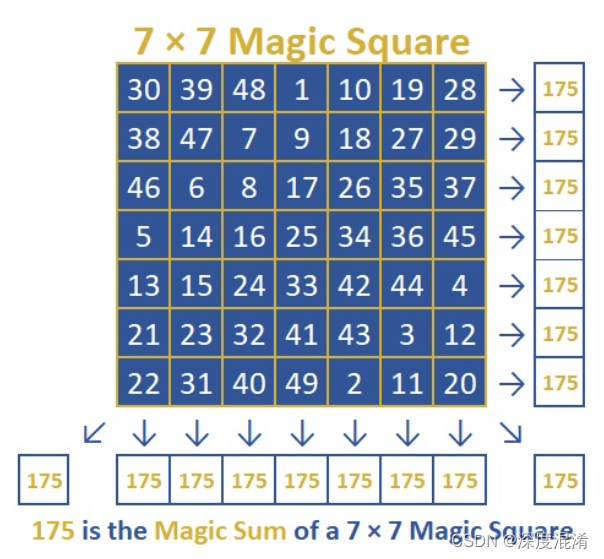
幻方(Magic Square)是一种将数字安排在正方形格子中,使每行、列和对角线上的数字和都相等的方法。
幻方也是一种中国传统游戏。旧时在官府、学堂多见。它是将从一到若干个数的自然数排成纵横各为若干个数的正方形,使在同一行、同一列和同一对角线上的几个数的和都相等。

幻方的历史纪录
在一个由若干个排列整齐的数组成的正方形中,正方形中任意一横行、一纵行及对角线的几个数之和都相等,具有这种性质的图表,称为“幻方”。中国古代称为“河图”、“洛书”,又叫“纵横图”。
九宫洛书蕴含奇门遁甲的布阵之道。九宫之数源于《易经》。幻方也称纵横图、魔方、魔阵,它是科学的结晶与吉祥的象征,发源于中国古代的洛书——九宫图。公元前一世纪,西汉宣帝时的博士戴德在他的政治礼仪著作《大戴礼·明堂篇》中就有“二、九、四、七、五、三、六、一、八”的洛书九宫数记载。洛书被世界公认为组合数学的鼻祖,它是中华民族对人类的伟大贡献之一。同时,洛书以其高度抽象的内涵,对中国古代政治伦理、数学、天文气象、哲学、医学、宗教等都产生了重要影响。在远古传说中,于治国安邦上也具有积极的寓意!包括洛书在内的幻方自古以来在亚、欧、美洲不少国家都被作为驱邪避凶的吉祥物,这种古代地域广泛的图腾应该说是极其少见的。1975年上海人民出版社出版的自然辩证法丛书《自然科学大事年表》,对于幻方作了特别的述说:“公元前一世纪,《大戴礼》记载,中国古代有象征吉祥的河图洛书纵横图,即为九宫算,被认为是现代‘组合数学’最古老的发现。”还附了全书唯一的插图!
2500年前,孔子在他研究《易经》的著作《系词上传》中记载了:“河出图,洛出书,圣人则之。”最早将数字与洛书相连的记载是2300年前的《庄子·天运》,它认为:“天有六极五常,帝王顺之则治,逆之则凶。九洛之事,治成德备,监照下土,天下戴之,此谓上皇。”明代数学家程大位在《算法统宗》中也曾发出“数何肇?其肇自图、书乎?伏羲得之以画卦,大禹得之以序畴,列圣得之以开物”的感叹,大意是说,数起源于远古时代黄河出现的河图与洛水出现的洛书,伏羲依靠河图画出八卦,大禹按照洛书划分九州,并制定治理天下的九类大法,圣人们根据它们演绎出各种治国安邦的良策,对人类社会与自然界的认识也得到步步深化。大禹从洛书中数的相互制约,均衡统一得到启发而制定国家的法律体系,使得天下一统,归于大治,这是借鉴思维的开端。这种活化思维的方式已成为科学灵感的来源之一。从洛书发端的幻方在数千年后更加生机盎然,被称为具有永恒魅力的数学问题。
十三世纪,中国南宋数学家杨辉在世界上首先开展了对幻方的系统研究,欧洲十四世纪也开始了这方面的工作。著名数学家费尔玛、欧拉都进行过幻方研究。
中国不仅拥有幻方的发明权,而且是对幻方进行深入研究的国家。公元13世纪的数学家杨辉已经编制出3-10阶幻方,记载在他1275年写的《续古摘奇算法》一书中。在欧洲,直到1514年,德国著名画家丢勒才绘制出了完整的四阶幻方。
而在国外,十二世纪的阿拉伯文献也有六阶幻方的记载,中国的考古学家们曾经在西安发现了阿拉伯文献上的五块六阶幻方,除了这些以外,历史上最早的四阶幻方是在印度发现的,那是一个完全幻方(后面会提到),而且比中国的杨辉还要早了两百多年,印度人认为那是天神的手笔.1956年西安出土一铁片板上所刻的六阶幻方(古阿拉伯数字)十三世纪,东罗马帝国才对幻方产生兴趣,但却没有什么成果.
直到十五世纪,住在君士坦丁堡的魔索普拉才把中国的纵横图传给了欧洲人,欧洲人认为幻方可以镇压妖魔,所以把它作为护身符,也把它叫作「Magic Square」.
任意阶幻方构造法,任意维幻方构造法,任意次幻方构造法,都早已找到。不存在最大阶幻方的世界纪录之类.对于各种媒体报导的幻方世界之最,很多是不实报导,不存在未解最大阶数幻方。
源程序
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Algorithm_Gallery
{
public static int[,] Magic_Square(int n)
{
int[,] magicSquare = new int[n, n];
int i = n / 2;
int j = n - 1;
for (int num = 1; num <= n * n;)
{
if (i == -1 && j == n)
{
j = n - 2;
i = 0;
}
else
{
if (j == n)
{
j = 0;
}
if (i < 0)
{
i = n - 1;
}
}
if (j >= 0)
{
if (magicSquare[i, j] != 0)
{
j -= 2;
i++;
continue;
}
else
{
magicSquare[i, j] = num++;
}
}
j++;
i--;
}
return magicSquare;
}
}
}
32幻方:
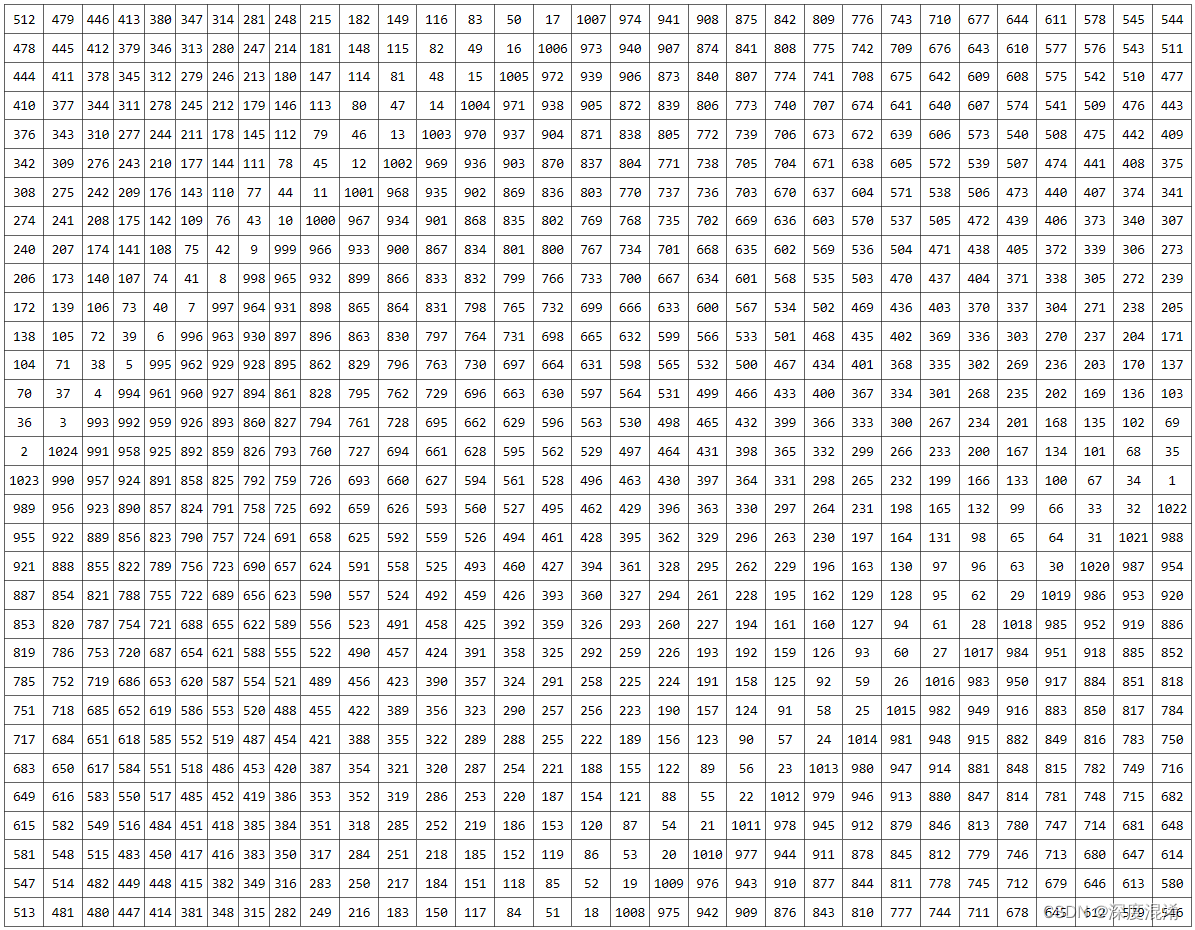
?128幻方:

?
