[数据结构与算法]矩阵链相乘（动态规划法）

矩阵链乘法是耳熟能详的问题了，有很多矩阵，排列成矩阵链，矩阵链的要求是相邻的两个是可以相乘的，可以相乘是有条件的，两个矩阵能够相乘的条件就是行、列之间是有关系的，两个矩阵如果能够相乘，就是前面矩阵的列号和后面矩阵的行号是一致的。 如何确定矩阵的乘法顺序，使得元素相乘的总次数最少。

一、问题描述

1、问题

设A₁ _,A₂ , … ,A_n为矩阵序列， A_i为 P_i-1 X P_i 阶矩阵，i = 1, 2, … , n. 试确定矩阵的乘法顺序，使得元素相乘的总次数最少。

2、输入：向量

$$P=<P_0,P_1,\dots ,P_n>，$$
$$其中P_0,P_1,\dots ,P_n为n个矩阵的行数与列数$$

3、输出：矩阵链乘法加括号的位置.

二、矩阵相乘基本运算次数

矩阵A： i 行 j 列，B: j 行 k 列，以元素相乘作基本运算，计算 AB的工作量

c_ts = a_t1 b_1s + a_t2 b_2s + … + a_tj b_js

AB: i 行 k列，计算每个元素需要做 j 次乘法, 总计乘法次数 为 i j k

Notes：两个矩阵相乘的工作量就是，A、B相乘得到C矩阵，C矩阵里面有i行k列个元素，每一个元素的计算是由列数j的地方的行数来决定的，j次的乘法，这里面有多少次元素j次元素相乘，每一个元素是由j次乘法决定的，一共有i 行 k列（ik）个元素，（ik）是它的总个数，每个元素个数要进行k次乘法，所以总计乘法次数 为 i j k

三、实例说明

1、实例

现在有三个矩阵，A₁，A₂，A₃
$$P=<10,100,5,50>,A1:10X100,A2:100X5,A3:5X50$$

最终乘完后是10 X 50的矩阵，这个时候做相乘有两种乘法顺序

（1）比如A₁，A₂先乘，乘法次数 为 i j k，需要10 X 100 X 50次乘法，（A₁ A₂）乘完之后的矩阵大小是10 X 5的矩阵，这个矩阵再和A₃相乘，它的乘法次数 为10 X 5 X 50，运算次数是7500次

（2）另外一种运算，先让A₂，A₃先乘，需要100 X 5 X 50次乘法，乘完之后的矩阵大小是100 X 50的矩阵，这个矩阵再和A₁相乘，它的乘法次数 为10 X 100 X 50，运算次数是75000次

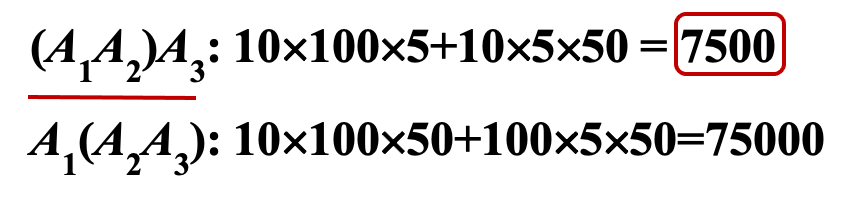
这两种乘法的次数明显差别非常大，第一种次序计算次数最少，次序的不同计算的次数也会不同，这个时候问题就变成了加括号的问题

2、蛮力算法

现在有n个矩阵，决定先乘的次序，量级是非常高的

3、动态规划算法

矩阵链里面的子问题就是将原问题划分成两段的时候，不管怎样分割，最后一次分割的位置一旦确定以后，原问题就变成了两段。

一个是在最后一次分割最后一次加括号的位置一定会分成左边和右边，左边这一段就是新的矩阵链相乘的问题，在这个里面依然存在要去找一个最好的括号化的方法（也就是往里面加括号），加入的括号能够得到最少的乘法的次数，然后原问题整个矩阵链从左边界到右边界分割成两段以后，原问题加括号的方法，在子问题里面加括号的方法加进去之后的乘法的次数，其实是一样的。

原问题的最优的加括号的方法一定也是也是子问题的最优的加括号的方法，否则我们就可以用剪切粘贴的方法来构成一个新的最优解，最优子结构就不满足了。

• 子问题划分
  A_i…j：矩阵链 A_i A_i+1 … A_j，边界i, j
  输入向量： < P_i-1, P_I, … , P_j>
  其最好划分的运算次数： m[i, j]
• 子问题的依赖关系
  最优划分最后一次相乘发生在矩阵k 的位置，即
  A~i …j~ = A_i…k A_k+1…j

A_i…j最优运算次数依赖于 A_i…k与 A_k+1…j 的最优运算次数

四、总结

动态规划算法设计要素 ：

• 多阶段决策过程，每步处理一个子问题，界定子问题的边界
• 列出优化函数的递推方程及初值
• 问题要满足优化原则或最优子结构性质，即：一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系