[数据结构与算法] 关于哈密顿路是否存在的遍历算法

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 关于哈密顿路是否存在的遍历算法 -> 正文阅读

[数据结构与算法]关于哈密顿路是否存在的遍历算法

一、前言

我是怎么也没想到这个问题陪伴了我快十年的时光，占到了我生命的一半时光（当然不可能一直在死磕这道题），十年中每每学到一些新的知识都会进行一些尝试，但很多时候还是无功而返，大概在十天前复习数据结构相关知识的时候偶然发现了一个简单而且有趣的公式，然后灵感就来了，不过有一点点遗憾的是身为学数学的出身的，未能使用纯数学的方式解决，有一点点丢人，话不多说，请看正文。

二、基本术语

这个问题涉及图论领域中的哈密顿路的问题，那首先先解释一下哈密顿路的定义。

哈密顿路：经过图G的所有顶点的路

好了，问题来了，那么路是啥？

路：路是一条途径，途径中的各个顶点不同

再套一波娃，途径是啥？

途径：非空顶点序列，要求顶点之间可以相连（就是可以走来走去的）

我们严格一点，简单图为例，顶点序列即可代表途径（最初的定义是点边交替序列）

简单图：无环和无两条连杆连接同一对顶点（即没有一条边的两个顶点相同和两条边的顶点相同这两种情况）

至此概念以及全部讲述完毕，接下来描述问题就容易多了。

度：对于无向图，即为每个顶点上边的数目

无向图：没有方向的图，一般研究的简单图默认就是无向图

三、问题及其衍生问题

在这里插入图片描述

先上图，原问题为：求画法，将所有红色的小点连起来不重复，即无重复点无重复边，且连起来的路的任意两条边只能为90度角，不允许出现45度角，若相邻两个点记为1，则不允许出现不为1的其他情况，下面给几个错误示范和成功示范。

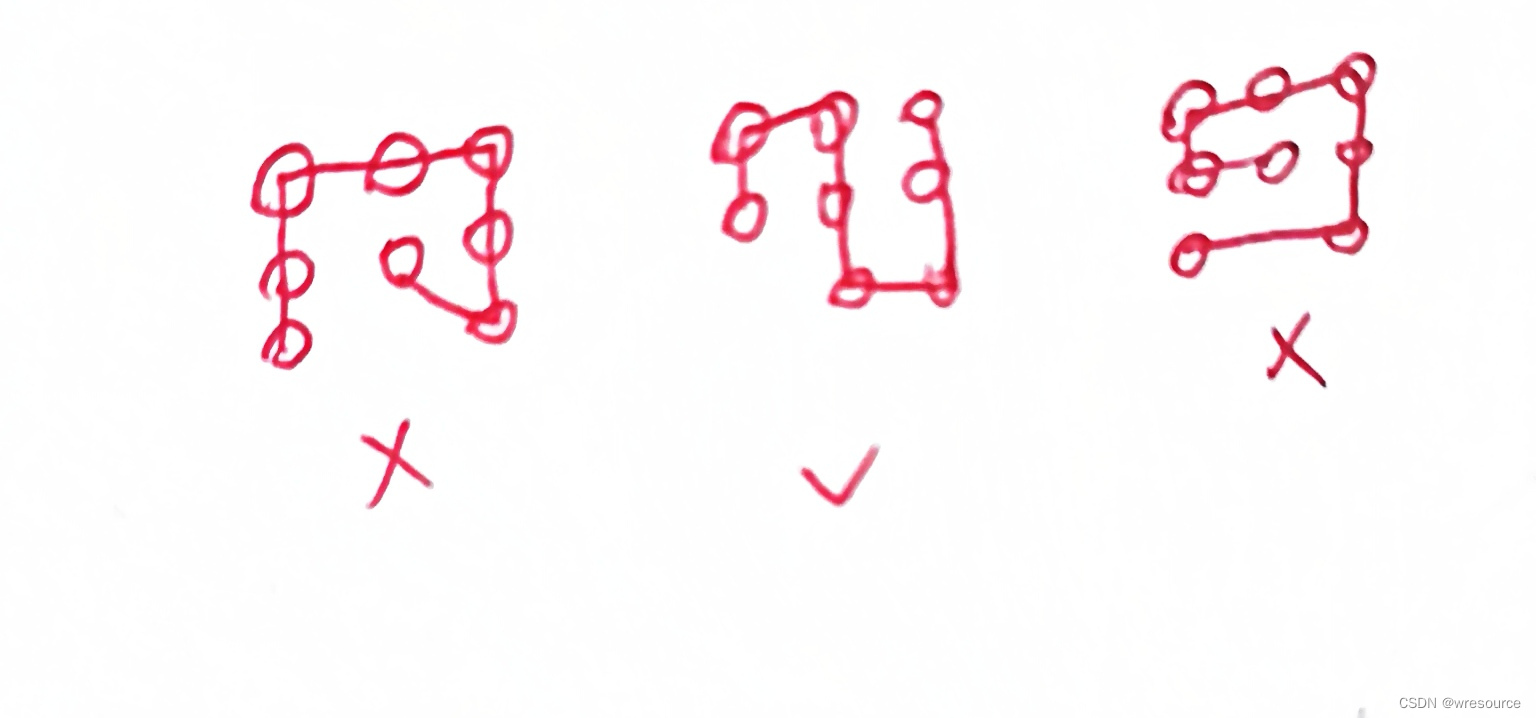
在这里插入图片描述

上面的定义看上去有点拗口，总而言之就是每次只能走一步的意思，出现45度的斜边和跨度为2的是不允许的（如果不是定义如此通俗易懂，感觉一二年级的小孩子也能做，我就不会记得这道题10年）。接下来给出比较严格的定义，对原问题进行了一点点转换。

下图是否有哈密顿路

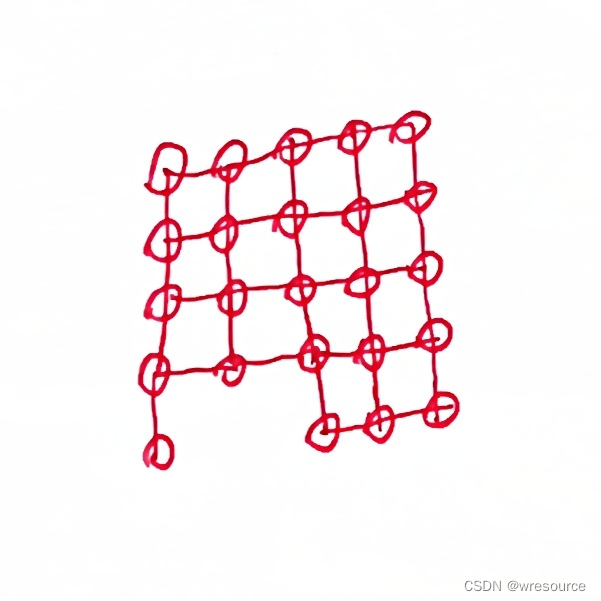
在这里插入图片描述

是不是非常简单的一道题，描述相当的清晰（不过这问题小孩子肯定看不懂）

可以尝试扩大维度，以及缺失点的位置判断是否有哈密顿路，大学之前，我通过观察法得出的结论如下

对于偶数阶的此类图，最外边一圈无论那个点缺失均存在哈密顿路
对于奇数阶的此类图，只有最外边一圈中缺失的点位于那条边的相对偶数位置不存在哈密顿路，奇数位置也是存在哈密顿路

存在的两种情况，利用数学归纳法即可证明，比较简单，但需要有一定的图论基础才可以写的相对规范，这里不进行说明，对于不存在的情况，目前我只能做到计算机求解低维，不过对于最初的那个问题已经解决。在上大学之前几乎没有任何工具可以解决这个问题或者靠近一点，不过可以想象，如果我当时给画出来，那么这个问题可能就不会在我心中挂起10年之久（这是个悲伤的故事）。

四、算法思想

算法思想还是比较简单的，只做了两件事，利用一个定理和进行运算符的重载。

定理（不晓得叫啥名字）

设图G的邻接矩阵为 $A$ ， $A^n$ 的元素 $A^n[i][j]$ 等于由顶点 $i$ 和顶点 $j$ 的长度为n的路径的数目。

这里的路径更严格一点说就是上述概念中的迹，你应该看到一点点眉目了，即将解决，这里不加证明的给出一个结论，上述图如果存在哈密顿路，则路的长度一定等于顶点数减1，意味着上面那个图需要走23步才能存在哈密顿路。那不是只要找出邻接矩阵，任何求其23次幂即可完成求解，由于此图的特殊性，其中有一个点必为起点或者终点，那么只需要检查矩阵第一行元素是否全为零即可完成证明？？当时看到这个定理后热血澎湃，晚上回来直接开电脑一顿乱敲，最后看到那个数据是10亿，我陷入了沉思，有点小失落，后面换成低阶的时候发现这个是迹（寄），可以重复走的，意味着可以重复走一条路，但这个定理真的形式上相当漂亮，一定会有方法的，所以最后也是基于这个定理，不过做了一点点小改进，然后利用c++的运算符重载实现的，最初是考虑matlab的，后面发现matlab在这个算法上几乎没有任何优势，原本是基于矩阵的，后面需要做比较大的运算符重载，以至于最纯粹的矩阵没有用到，遂放弃，改c++。经过上面的简要算法介绍相信你应该对于算法有了一个基本的轮廓，接下来开始一步步刨析算法。

1.定理证明刨析

**设图G的邻接矩阵为 $A$ ， $A^n$ 的元素 $A^n[i][j]$ 等于由顶点 $i$ 和顶点 $j$ 的长度为n的路径的数目。**这个定理的证明理解是算法能够成功实现的关键，定理的本质上就是模拟寻路的过程，比如 $A [i] [j]$ 代表第 $i$ 个点到第 $j$ 点是否相连，将 $A ? A$ 的元素展开，例如 $A^2[1][1] = a_{11}*a_{11} + a_{12}*a_{21}...$ 后面就不再展开了，每一个式子本质上是一条路径， $a_{11}*a_{11}$ 代表迹:1 1 1, $a_{12}*a_{21}$ 代表迹:1 2 1,以此类推，由于矩阵的特性，所以每次成一个矩阵代表走一步的意思，如果这些式子不进行合并的话，那么下一次 $A^3[1][1] = a_{11}*a_{11}*a_{11} + a_{12}*a_{21}*a_{11}...$ ，如果你继续写下去就会发现这个本质上就是一个探索全部路线的一个过程，这个定理的巧妙之处就是它没有记录之前路径的信息，所以它的运算非常高效，它仍然可以作为此题排除点的一个好办法，这个运算无论是时间还是空间复杂度，如果不加干预将达到可怕的 $o(n^n)$ ,这不是我们想看到的，定理对这种情况进行整合，使得每次进行矩阵运算时的时间和空间复杂度都是一样的，但它抛掉了所有的信息即路径的信息，所以基于以上定理，稍微做了一点点改进，保留路径信息同时尽量使得算法高效。

2.改进后的算法

说实话在没跑之前，我是非常担心电脑万一给挂了咋整，所以在设计算法的时候非常小心（这也是非常苦恼的），最后解决上述问题大概花了10秒左右。我们要达到以下目标：

保留矩阵的运算过程，尽量少做修改，保持理论上的可行性
最后的运算结果包含路径信息

2.1 重定义类型

supperInt：这里重新定义了一种类型，包含一个int类型的数值，用于路径数目的计数，一个线性表，存放当前位置路径的集合，这里的类型相当于矩阵中的一个int型的元素，只是这里携带了路径信息。

commonInt：这是对于矩阵计算中需要下一个元素的当前下标设计的，这个类型用于辅助正常矩阵中元素的计算，包括一个int类型的数值和一个下标（也是int类型的）

2.2 重载运算符

这里重载运算符的目的是为了保持算法的有效性，同时减小出错的可能性

乘法运算符的重载

左操作数：supperInt

右操作数：commonInt

这里出现的场景为矩阵运算里面具体元素的相乘，不过你可能会有疑问，两个操作数类型为啥不同，这个稍后解释
加法重载运算符

左操作数：supperInt

右操作数：supperInt

这个也是矩阵运算过程中出现的加法，然后进行重载
矩阵乘法的重载

左操作数：vector

右操作数：int $n [d i m e] [d i m e]$

一个是列向量一个是矩阵

3.具体运算流程

当我们重载完毕之后就可以按照上述方式进行计算，不过这个问题比较特殊，我们只需要用一个行向量和一个矩阵进行运算，这个前提就是我们可以不加证明的给出哈密顿路的起点或者终点必为那个度为1的点。这里给出一个例子

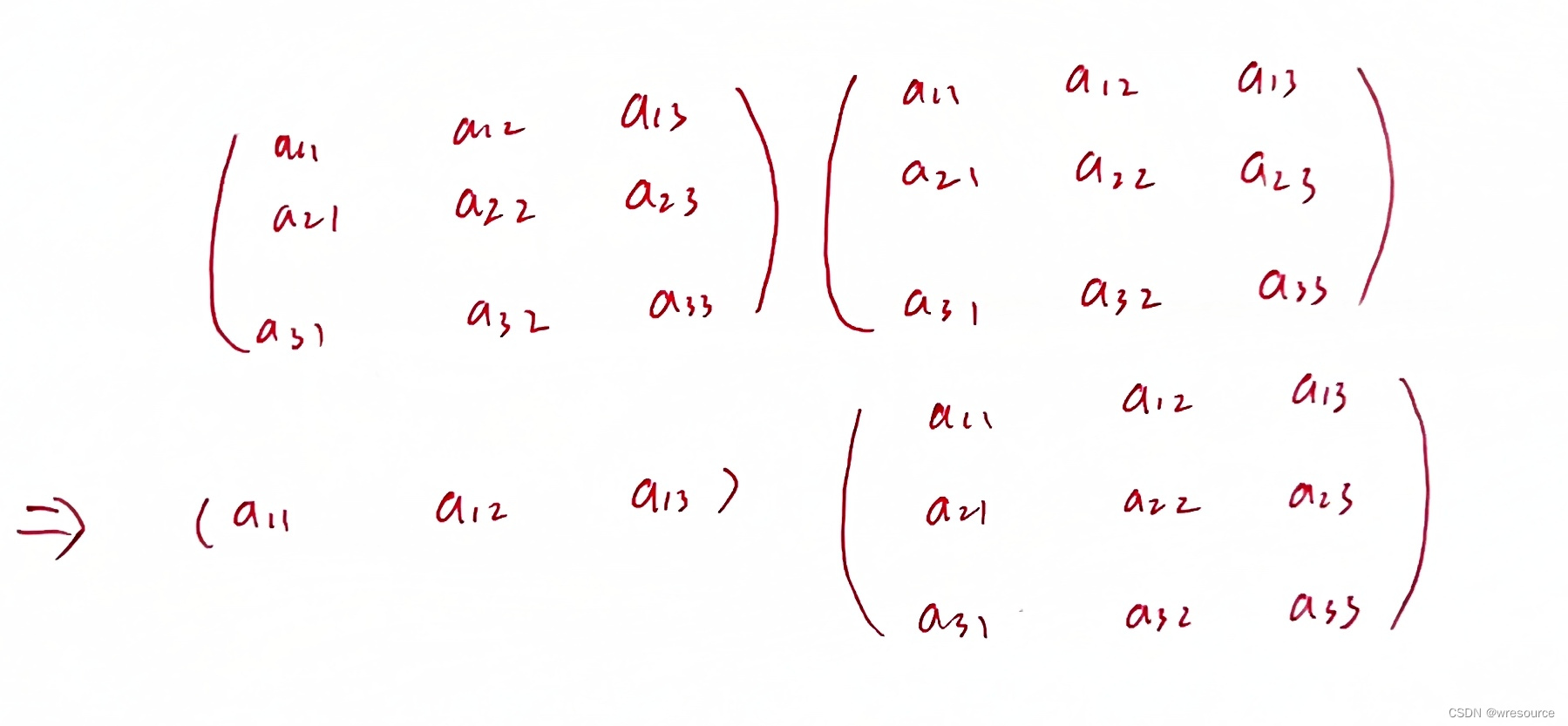
在这里插入图片描述

这里是考虑到后续的矩阵计算都用到其他行的数据，只用行向量和矩阵相乘可以大大减小计算量，应该可以理解上述重定义的类型吧，左侧的之所以还是考虑使用矩阵很大一个原因是考虑到空间复杂度，下标其实可以利用天然的二维数组的优势进行获取，但考虑到重载的时候两个元素相乘，如果不另外定义一个下标会非常乱，不好管理。这样的话，乘一个矩阵就是前进一步的意思

4.关键算法

这里最关键的算法核心思想在于上面那个乘法运算符的重载左操作数：supperInt 和右操作数：commonInt的那个

supperInt有一个value值，负责存储路径数目
supperInt中的一个线性表负责存储路径
commonInt中的value负责存储值，这个值即原始邻接矩阵中的值
commonInt中的index代表下一步的去向，即到那个点，value为0代表到不了，反之代表可以到

由于邻接矩阵是个稀疏矩阵故存在大量的0值，故算法为了快速排除，只要supperInt和commonInt中有一个值为0，运算结束，同时进行清理内存操作，当二者均大于0时进行下一步。

这一步主要是做排除非法的路径操作，可能你在代码中没有发现任何乘法的计算，不用担心，这个实质上是由于邻接矩阵只有0和1两种数值，这里转换成逻辑判断罢了，对于supperInt中的每个路径进行检查，用将进行乘法操作的commonInt中的下标值进行查询，若路径包含此下标，该路径直接删除即可，当时踩了一个坑，最初的想法是用set集合，set集合有个天然的唯一性的保证，只需要插入之后进行长度判断即可，后面发现路径不对劲，原来set集合内部自动有序，路径这样被自动排序就不是最初的那条了。这里你可能会有点疑惑，如果运气不好排除的不好不是爆炸，其实这也是我当时的顾虑，现在想想，可能是由于稀疏矩阵吧（还有可能就是电脑给力）。

可能你看完算法思想会觉得这个好像非常容易的样子，只用到一个线性表保存路径，其他的都挺简单，哈哈哈哈哈，我也是这么想的，这个想法大概一个上午当时就定好了，然后面对一张纸实际开始的时候还真的挺难受的（可能还有一个原因就是很久没碰c++了）。

五、算法实现步骤

接下来就是代码了，相信看完算法思想，这部分应该很容易理解，代码不多，重载花了100行，主函数100行，用到的库和命名空间声明，声明了一个维度值的宏。

#pragma once
#include<vector>
#include<iostream>
#include <algorithm>
#define dime 24
using namespace std;

1.类型定义

这里利用结构体和类分别对于两个类型进行定义，重载运算符作为友元放在supperInt类中，这里的类型用到了vector，是stl中的一个模板类，支持数组一样的下标访问方式，其他的还没试，虽然感觉可能差不多，这里这样定义够用，没去细究。（最开始想过自己定义一个链表实现，果然还是太天真了，这里吹爆stl，计算性能没让我失望）

typedef struct commonInt {
	//具体值
	//这里取值只有0和1
	int value = 0;

	//下标
	int index = 0;
}commonInt;

class supperInt {
public:
	//value为路径数目
	int value;
	
	//具体路径
	vector<vector<int>> path;
	supperInt() {
		this->value = 0;
	}

	//重载的两个友元函数
	friend supperInt operator + (supperInt s1, supperInt s2);
	friend supperInt operator * (supperInt s, commonInt c);
};

2.加法重载

本质上是两个线性表的合并，然后对于数值进行逻辑上的加和，这里你可能要问，vector自带一个成员函数size()为啥不用，这就是个悲伤的故事，这部分是初始化数组时发现的，如果不设置逻辑空值，会导致意外的bug(野指针，删除时元素时发生)的发生，同时为了保持最初的重载目的，所以还是保留了这个value值

//加法重载，本质上是线性表合并
supperInt operator+(supperInt s1, supperInt s2)
{
	supperInt s3;
	s3.path.insert(s3.path.end(), s1.path.begin(), s1.path.end());
	s3.path.insert(s3.path.end(), s2.path.begin(), s2.path.end());
	s3.value = s1.value + s2.value;
	return s3;
}

3.乘法重载

乘法重载最主要的目的就是排除，减少后续计算花费的时间，这里当时对于vector不熟悉，导致出现了较多的意外状况，不过可以放心的是下列代码都是可以执行的（经过了至少百万次运算的实践汪汪.jpg）。

//乘法重载，主要是排除不符合的路径
supperInt operator*(supperInt s, commonInt c)
{
	//对于值为0的快速排除，提高运算速度
	if ((c.value == 0) || (s.value == 0)) {

		//释放内存操作
		s.path.clear();
		s.path.swap(s.path);
		s.value = 0;
	}
	else {
		//一个个遍历检查，遇到重复的直接排除掉，并销毁内存
		for (vector<vector<int>>::iterator it = s.path.begin(); it != s.path.end();) {
            
            //find函数是库<algorithm>中的一个外部函数，用于查找值
			vector<int>::iterator result = find((*it).begin(), (*it).end(), c.index);
			if(result == (*it).end()){
				(*it).push_back(c.index);
				
				//循环内部++避免野指针
				it++;
			}
			else {

				//不符合的移除
				//然后逻辑上的value值--
				it = s.path.erase(it);
				s.value--;
			}
		}
	}
	return s;
}

4.矩阵乘法重载

这部分最坑的一个部分应该是对于矩阵运算的理解失误导致踩了一些坑，行向量是重复运算的，不应该被改变，需要自定义一个额外的向量进行保存。还有一点就是数组作为入参，需要比较完整的定义，其实也可以将二维数组换成类似vector的二维数组，这样就会统一一点，不过考虑到性能上，这部分越简单越好。

//矩阵乘法重载，这里需要注意的就是需要重新创建一个vector防止原数组丢失
//局限性就是n数组必须指定大小
vector<supperInt> operator *(vector<supperInt>& s1, int n[dime][dime]) {
	
	//复制一个s2保持运算过程中数组的不变性
	//这里复制采用copy性能略优于直接复制
	vector<supperInt> s2;
	s2.resize(s1.size());
	copy(s1.begin(), s1.end(), s2.begin());

	
	for (int i = 0; i < dime; i++) {
		supperInt sum;
		for (int j = 0; j < dime; j++) {

			//对于矩阵中的元素包装成commonInt类型
			//利用天然的数组下标节省内存
			commonInt t;
			t.index = i;
			t.value = n[j][i];

			//利用上面的运算符重载进行计算
			sum = sum + s2[j] * t;
		}
		//第i个矩阵运算的结果
		//这里会发生改变，故上述使用了一个临时数组
		s1[i] = sum;
	}
	return s1;
}

5.主函数文件

在此之前需要做一些记号，便于矩阵的赋值和最后路径的输出，这个记号随意就行，主要是方便自己，但也要统一

在这里插入图片描述

5.1 初始化

这里做的比较差的是矩阵初始化没有去找规律赋值，写了比较多的重复代码

//初始化一维数组
#define dim 24
#define step 23

vector<supperInt> target(dim);

//压入第一个初始路径
vector<int> ss;
ss.push_back(0);
ss.push_back(1);
target[1].path.push_back(ss);
target[1].value = 1;


//初始化矩阵
int A[24][24] = { 0 };
A[0][ 1] = 1;
A[1][ 2] = 1; A[1][ 5] = 1;
A[2][ 3] = 1; A[2][ 6] = 1;
A[3][ 4] = 1; A[3][ 7] = 1;
A[4][ 8] = 1;
A[5][ 6] = 1; A[5][ 10] = 1;
A[6][ 7] = 1; A[6][ 11] = 1;
A[7][ 8] = 1; A[7][ 12] = 1;
A[8][ 13] = 1;
A[9][ 10] = 1; A[9][ 14] = 1;
A[10][ 11] = 1; A[10][ 15] = 1;
A[11][ 12] = 1; A[11][ 16] = 1;
A[12][ 13] = 1; A[12][ 17] = 1;
A[13][ 18] = 1;
A[14][ 15] = 1; A[14][ 19] = 1;
A[15][ 16] = 1; A[15][ 20] = 1;
A[16][ 17] = 1; A[16][ 21] = 1;
A[17][ 18] = 1; A[17][ 22] = 1;
A[18][ 23] = 1;
A[19][ 20] = 1;
A[20][ 21] = 1;
A[21][ 22] = 1;
A[22][ 23] = 1;

//下三角的赋值
for (int i = 0;i < dim;i++) {
    for (int j = 0; j < i; j++) {
        A[i][j] = A[j][i];
    }
}

5.2 开始计算

这部分就非常简单了，有了之前的运算符重载，现在非常容易

//开始逻辑计算
//这里的步数可以调整，正常时步数-1次循环，判断是否有哈密顿路，第一步在初始化中已经完成了
for (int i = 0; i < step - 1; i++) {
    target = target * A;
}

5.3 展示结果

这部分做了一些输出显示

//计算解决方案数
int sum = 0;
for (int i = 0; i < dim; i++) {
    sum = sum + target[i].value;
}


cout << "总的解决方案数:" << sum << endl;
cout << "每个解决方案所用的步数:" << step << "步" << endl;
for(int i= 0;i < dim;i++){

    cout << "从1结点到达" << (i + 1) << "结点的解决方案数目：" << target[i].value << "\n";

    for (int j = 0; j < target[i].path.size(); j++) {
        for (auto it = target[i].path[j].cbegin(); it != target[i].path[j].cend(); it++)
        {
            cout << (*it + 1) << " ";
        }
        cout << "\n";
    }
    cout << "\n";
}

哈密顿路的验证结果展示，这个结果说明此图无哈密顿路

在这里插入图片描述

当然，可能这稍微缺乏一点点说服力，所以我们退一步，改一下参数，换成22步看看结果，这些即全部完成22步无重复的路径，也就意味着下一步其实，我们只要验证1064种情况即可证明是否存在哈密顿路，不过这里就不一一说明了，至此已完成计算机对于此问题的证明。理论依据即上面的那个定理。

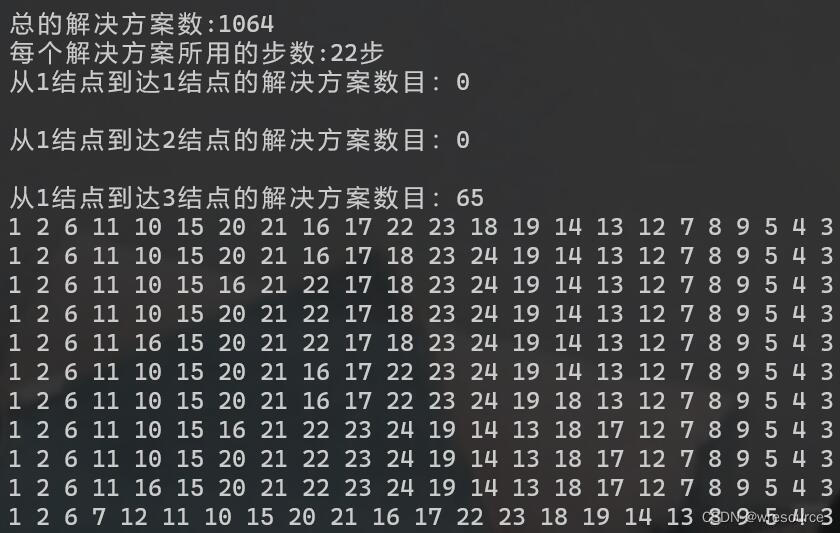
在这里插入图片描述

有点长，就不完全截下来了，可以保存到文件里面，方便查看和校正。

六、时间和空间复杂度分析

算法主要耗时的部分应该就是乘法重载部分，原定理的算法复杂度只有 $o(n^3)$ ,而此算法不仅增加了时间复杂度同样也增加了空间复杂度，具体复杂度暂时还未进行计算，不过有预感这个复杂度应该是可以计算的，因为矩阵是稀疏矩阵，且非常的对称，这部分主要是乘法重载过程中的遍历路径判断过程相当耗时，不过乐观的是，空间复杂度并没有想象中的越来越大，反倒是越后面越少，应该存在某种联系。

七、算法的缺点以及值得改进的地方

1.算法缺点

算法时间复杂度应该是值得吐槽的一个地方，目前还未进行严格计算，这个就像薛定谔的猫，电脑指不定哪天跑的时候给挂了,算法未能应用比较高效的图论相关的结论，说实话这次能跑出来就是极大的幸运。

2.值得改进的地方

其实最初的想法是利用矩阵变换完成计算，即通过添加矩阵完成计算，这样的话可以借助matlab高效的矩阵计算完成验证，只有 $o(n^3)$ 的时间复杂度和完全可以忍受的 $o(n^2)$ 的空间复杂度，但事实上有一个非常致命的问题，要完成这类操作，必须需要之前结点的信息，这样才可以查询是否重复，两全其美的方法看起来很难得样子。