IT数码购物网址头条软件日历阅读图书馆

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放器↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 基础30讲第18讲三重积分、曲线曲面积分 -> 正文阅读

[数据结构与算法]基础30讲第18讲三重积分、曲线曲面积分

目录

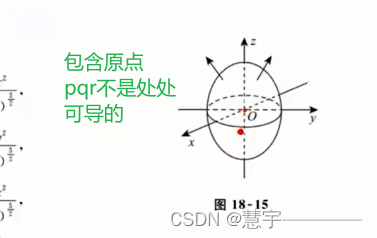
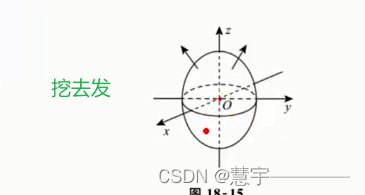
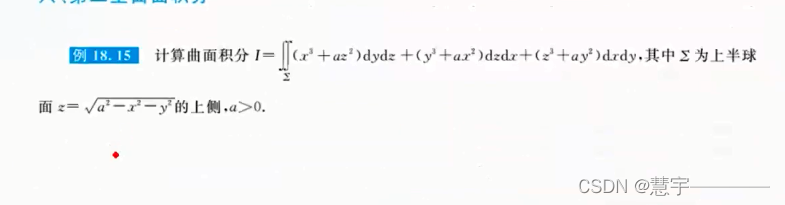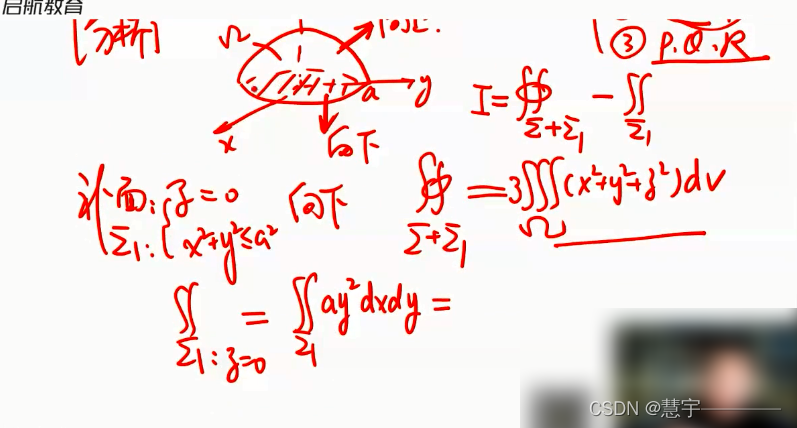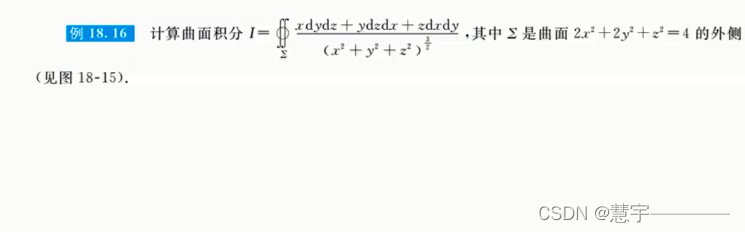综述区别于数一数二以计算为主
1、三重积分
2、第一型曲线积分
3、第一型曲面积分
4、应用(二重积分三重积分曲线曲面积分)
5、第二型曲线积分
6、第二型曲面积分

综述区别于数一数二以计算为主

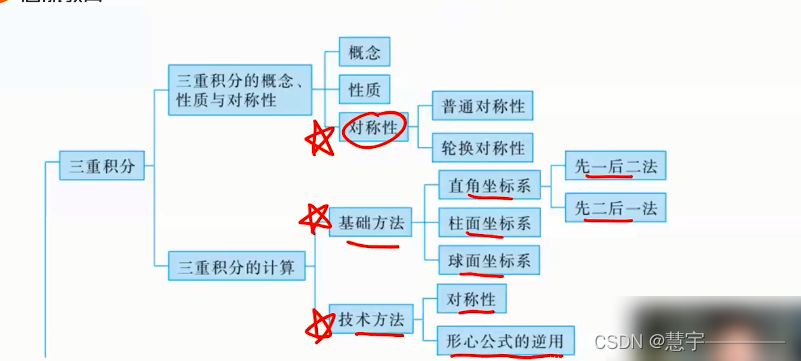
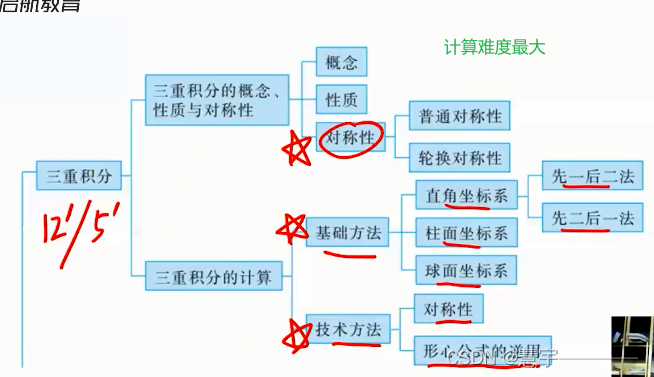
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

1、三重积分

1.1 三重积分的概念性质与对称性

1.1.1 概念

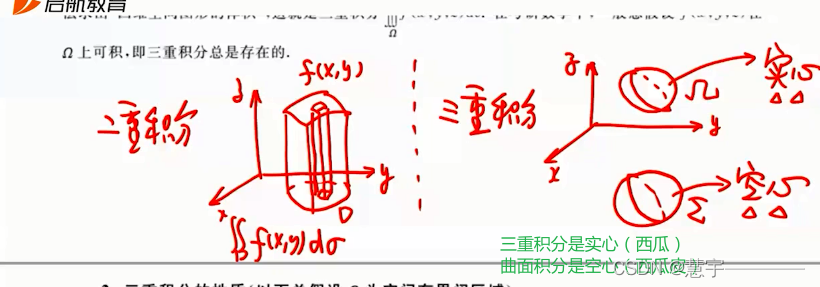
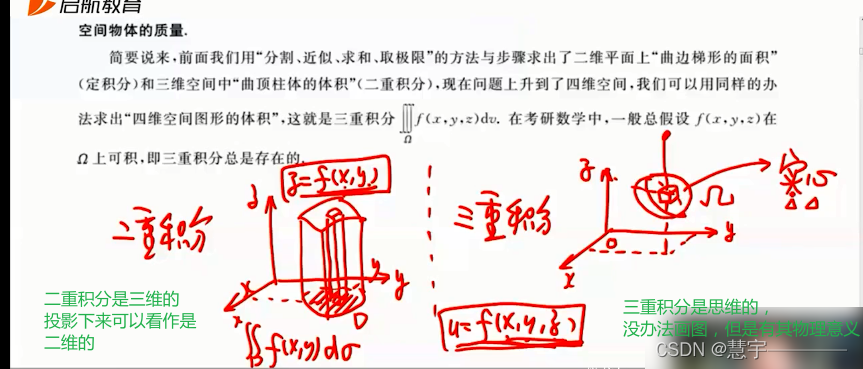
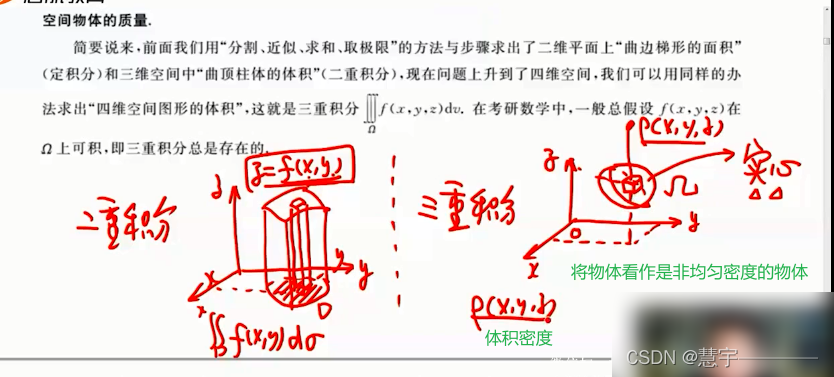
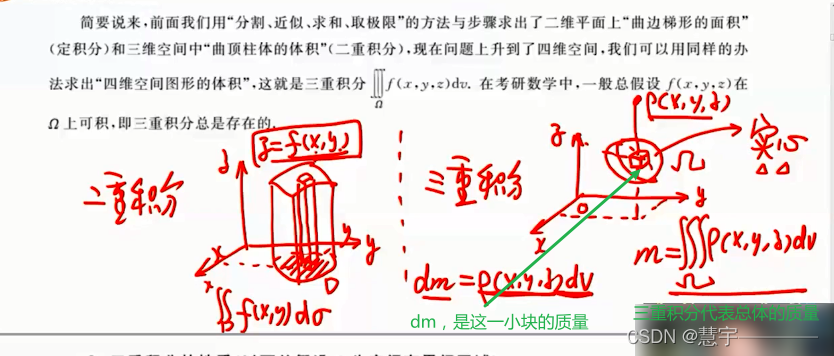
在这里插入图片描述

1.1.2 性质

1.1.3 对称性

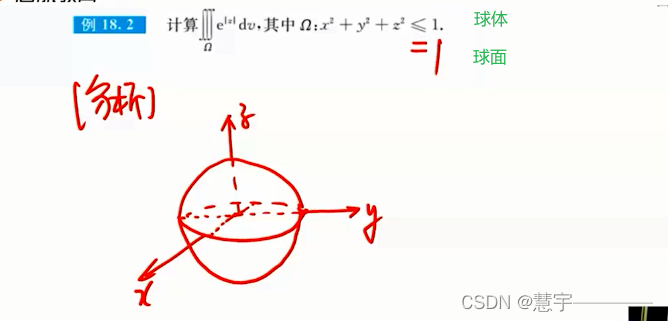
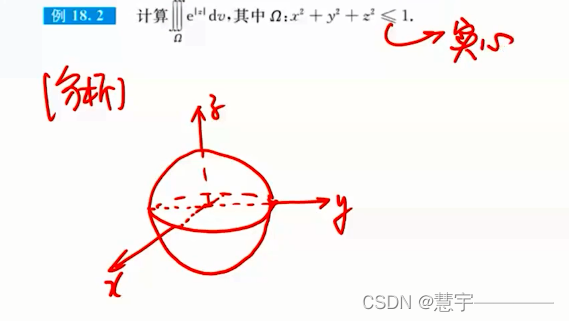
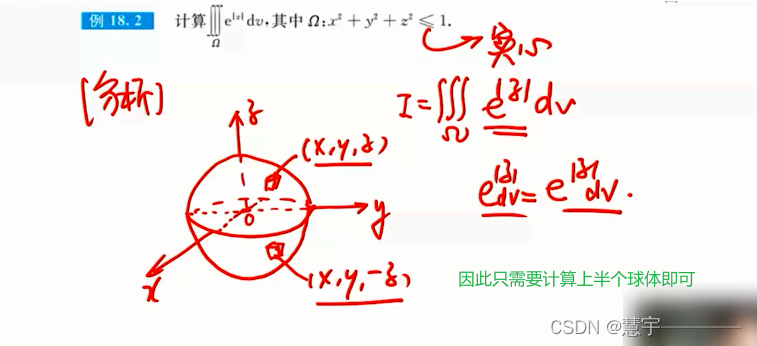
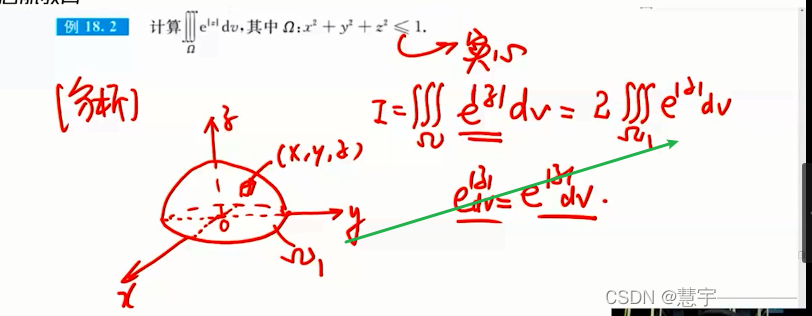
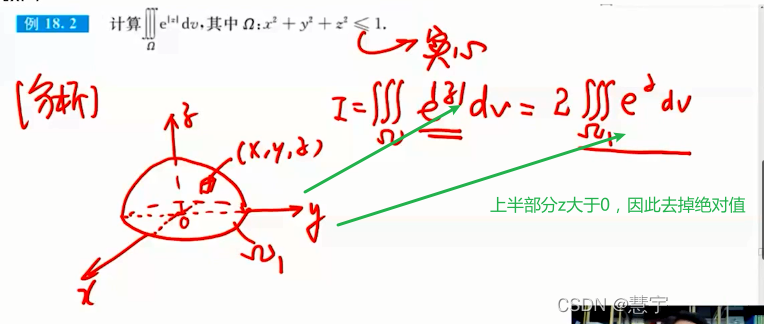
在这里插入图片描述

普通对称性

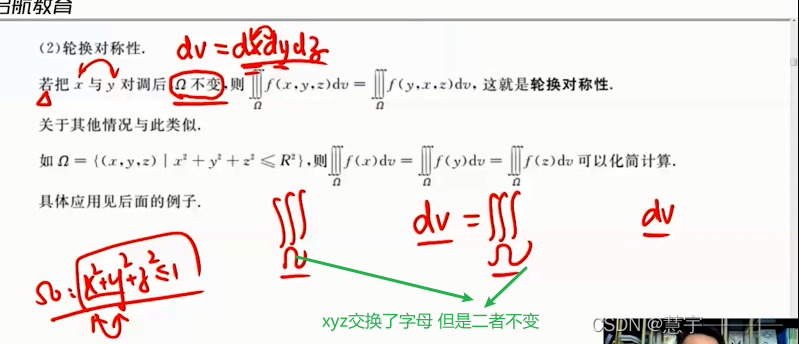
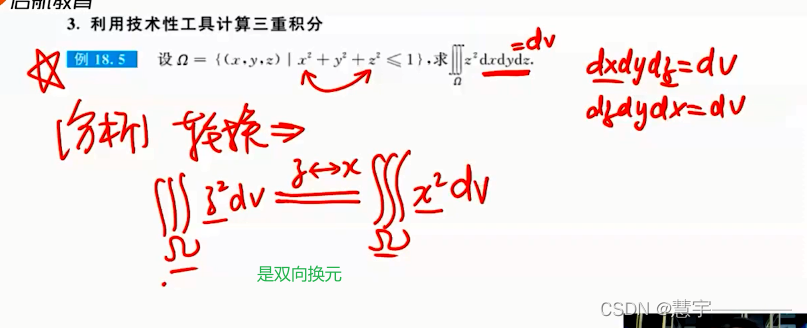
在这里插入图片描述

轮换对称性

在这里插入图片描述

1.2 三重积分的计算（化为定积分+二重积分）

1.2.1基础方法

在这里插入图片描述

直角坐标系（投影穿线法）

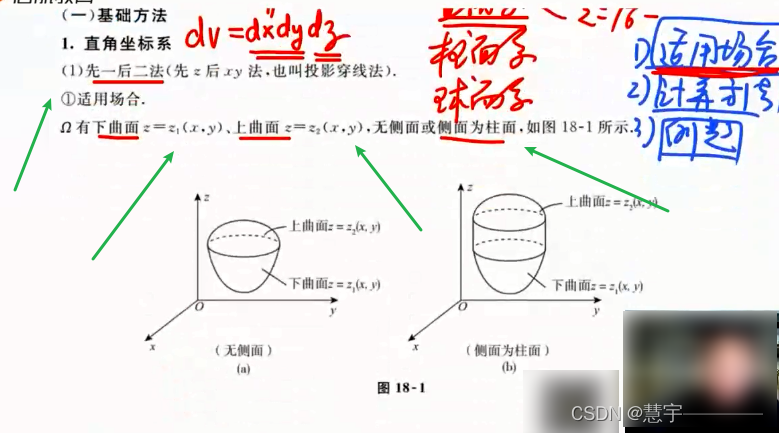
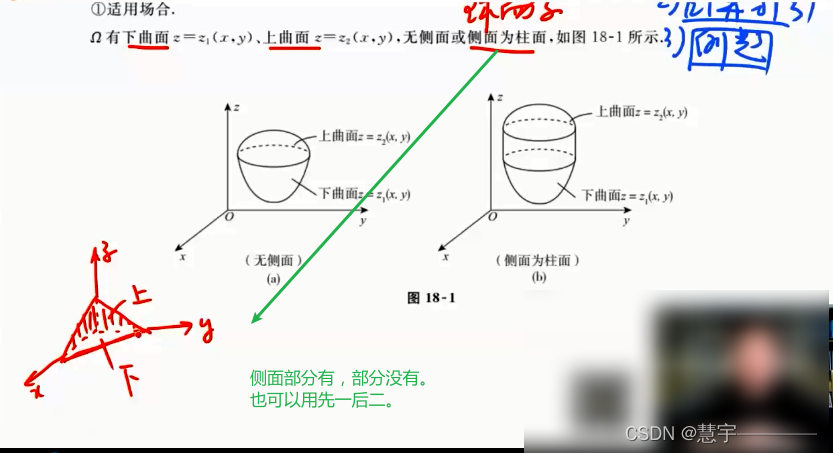
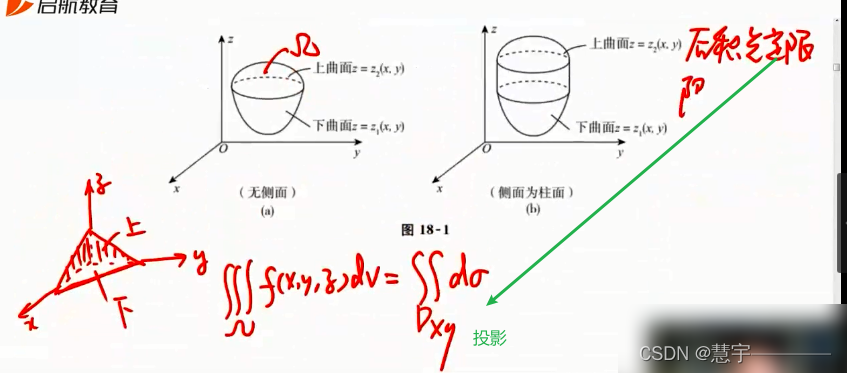
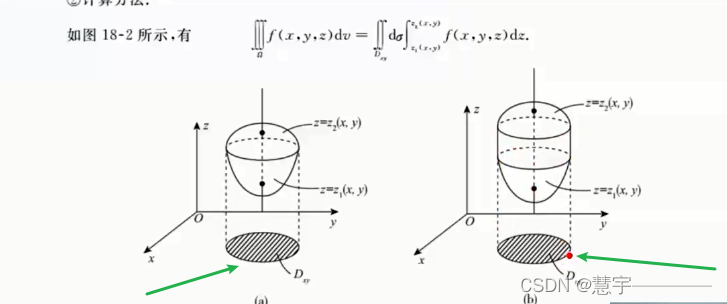
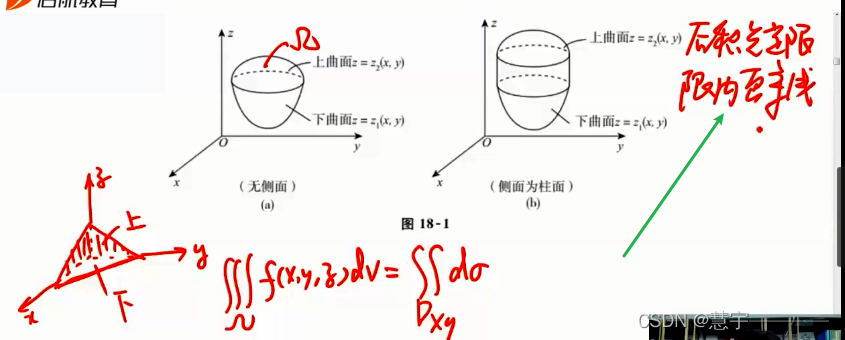
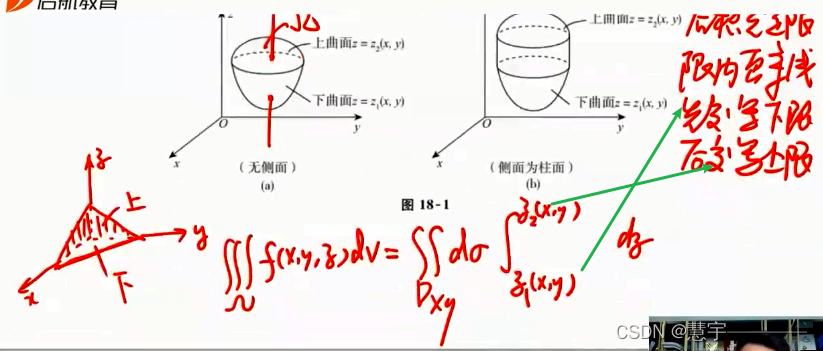
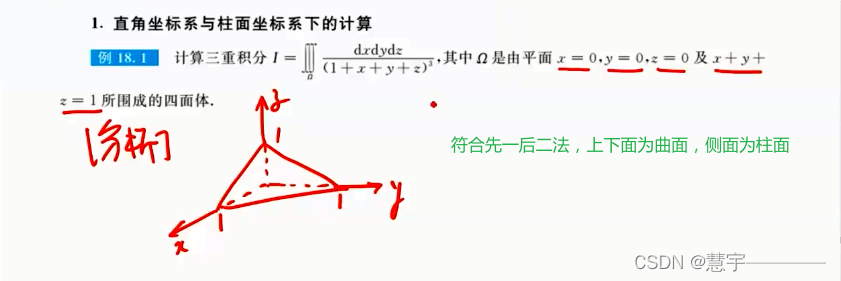
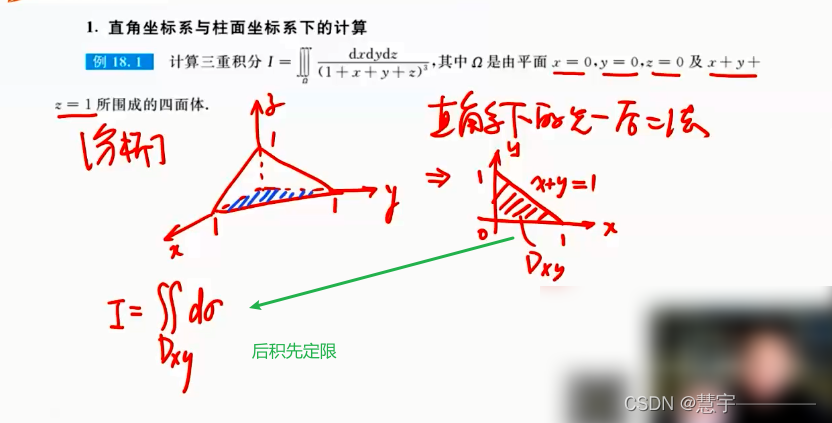
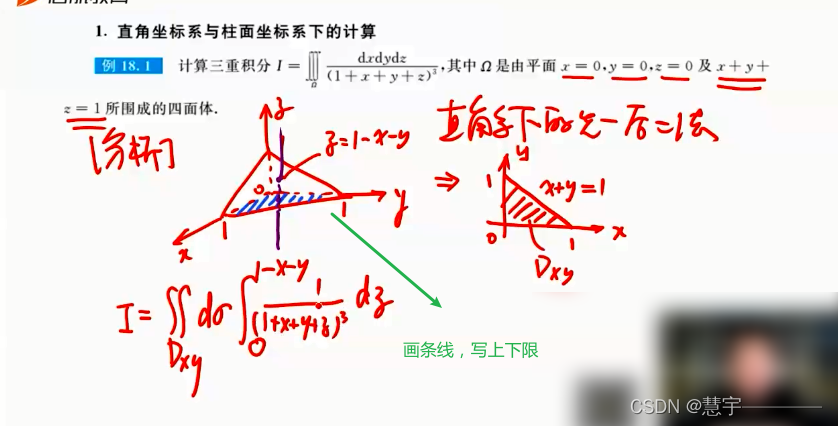
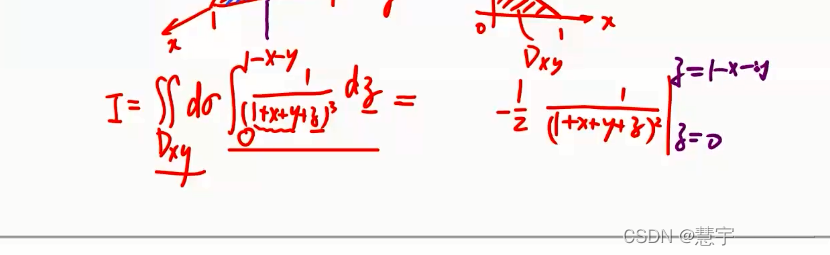
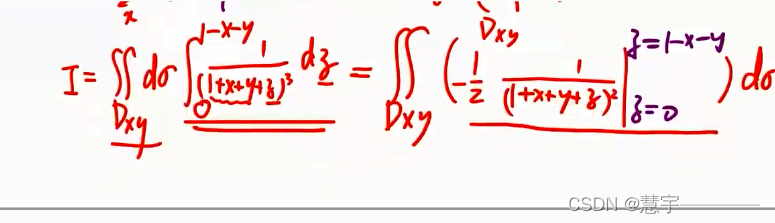
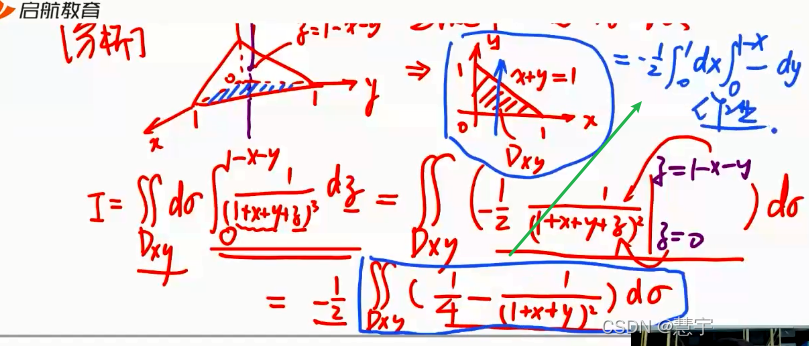
在这里插入图片描述

先一后二法

在这里插入图片描述

在这里插入图片描述

先二后一法（定限截面法）

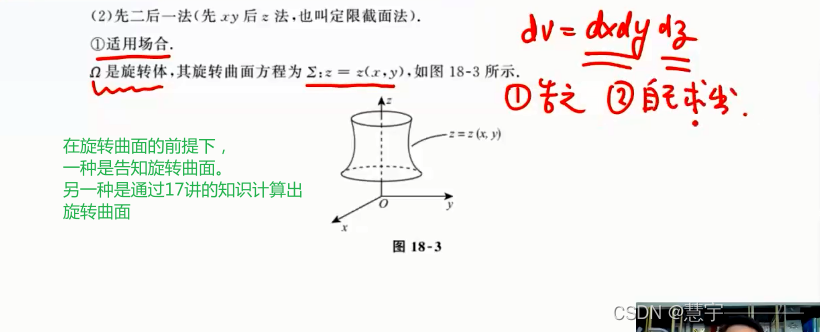
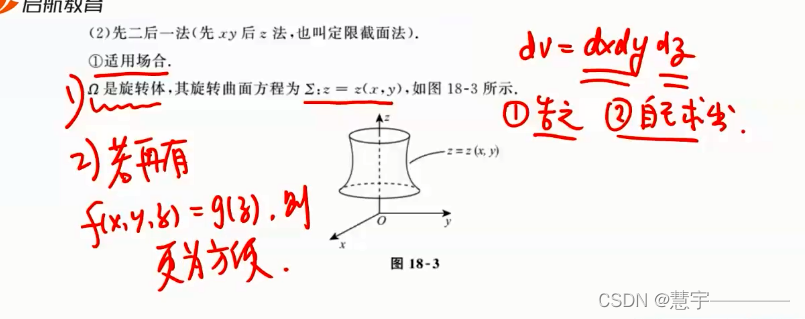
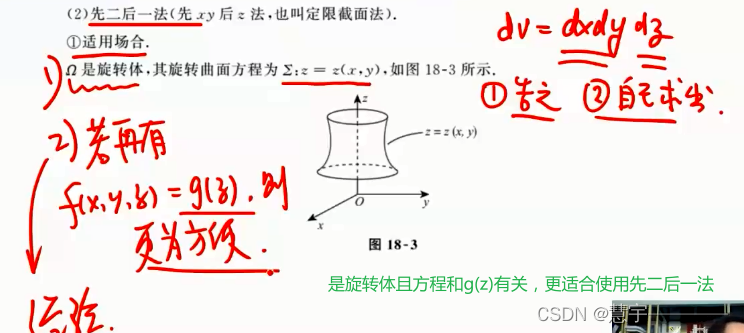
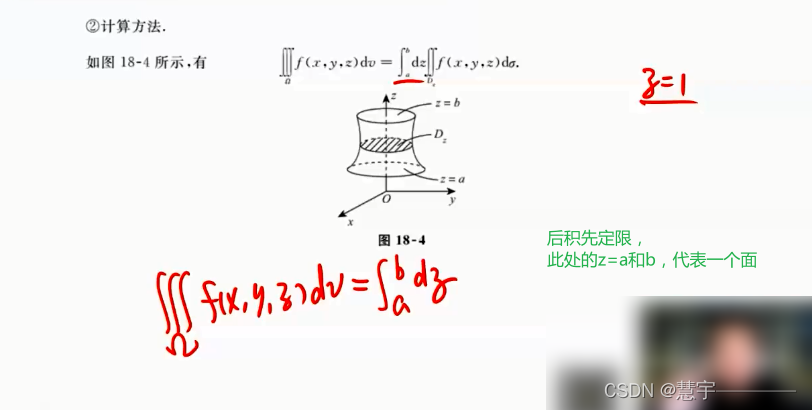
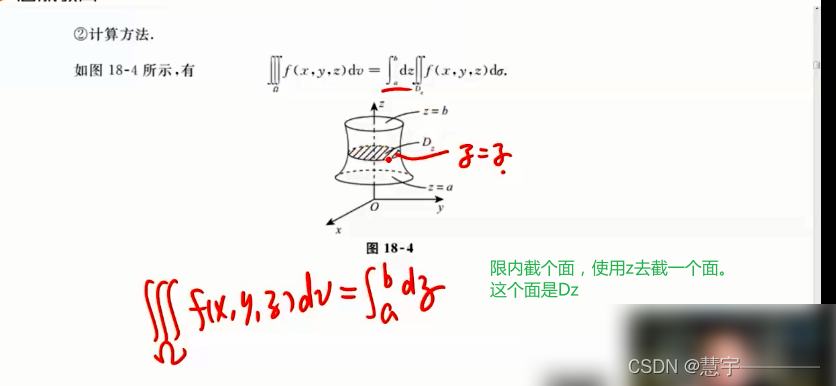
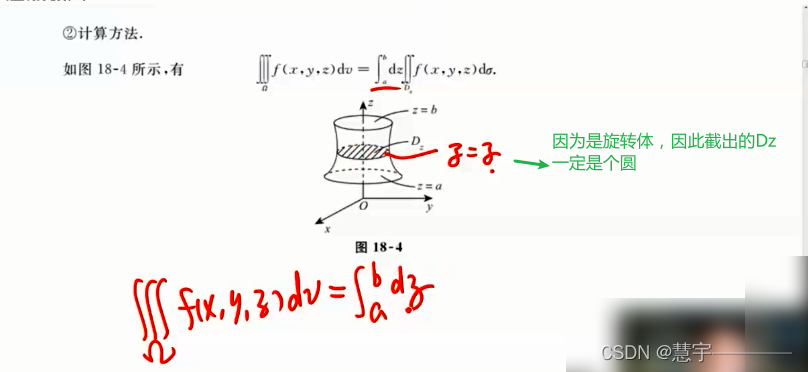
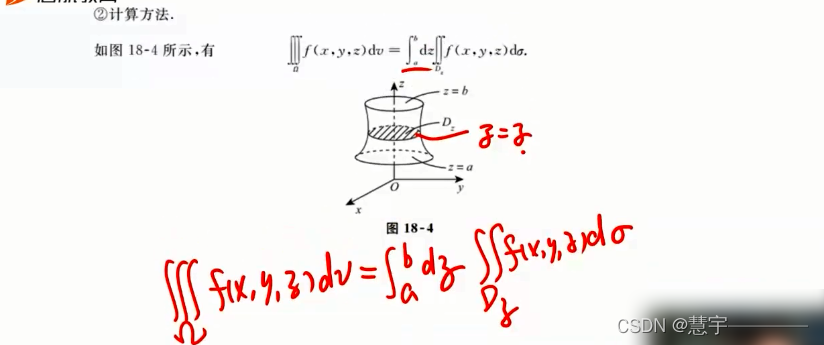
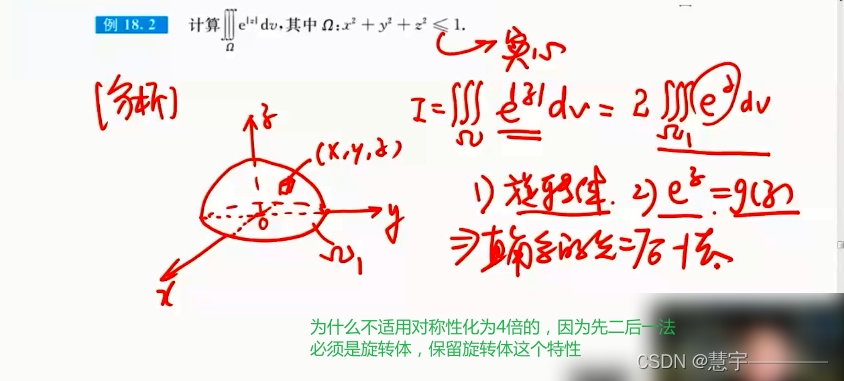
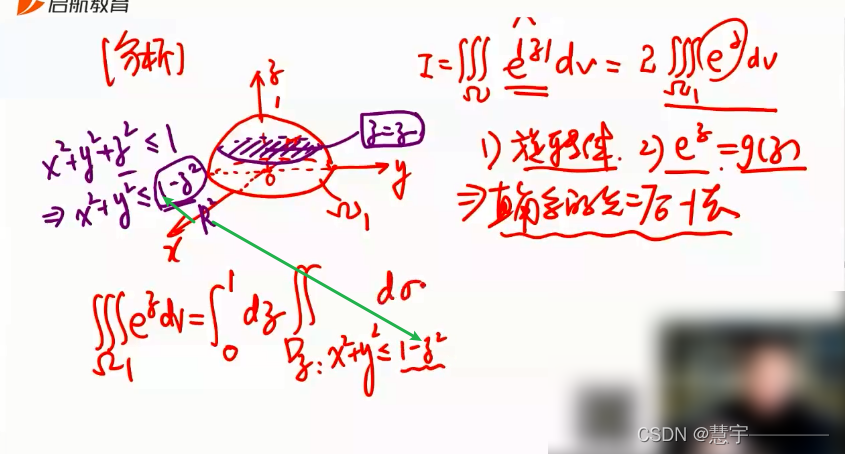
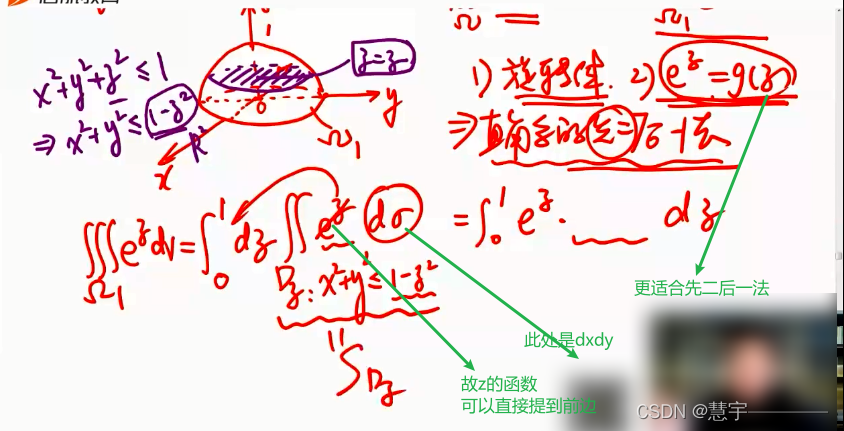
在这里插入图片描述

柱面坐标系（投影是部分圆，类似二重积分的极坐标系积法）

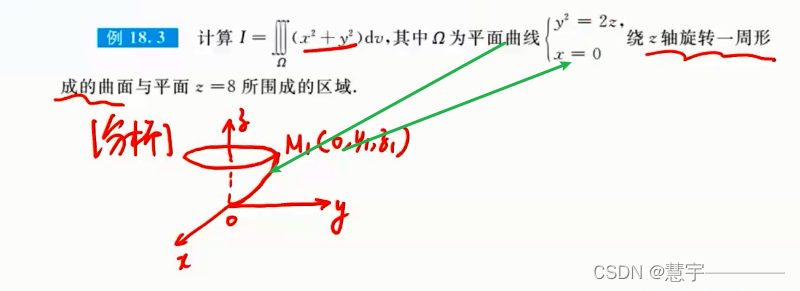
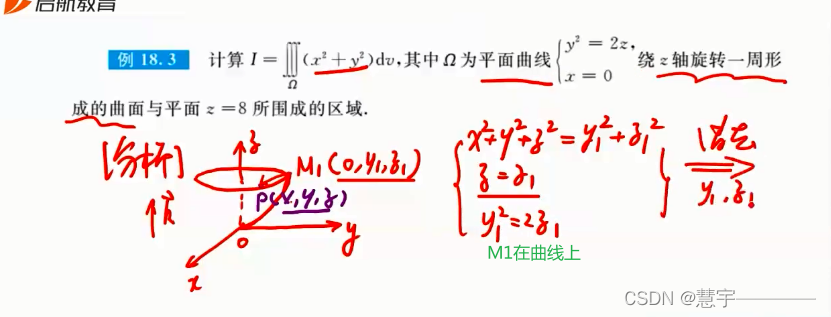
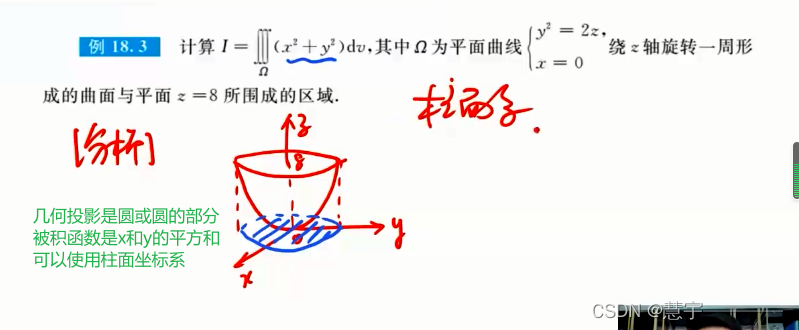
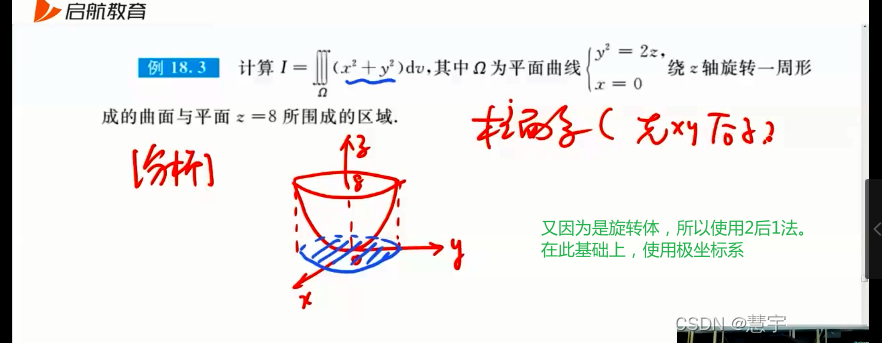
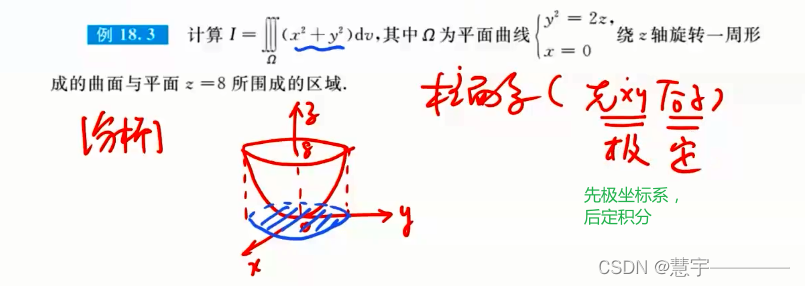
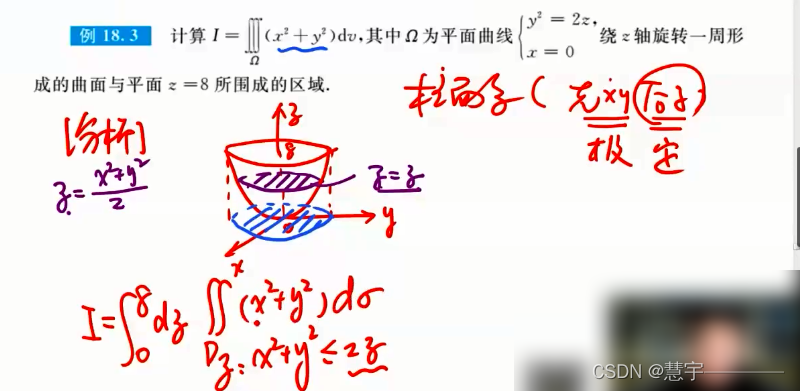
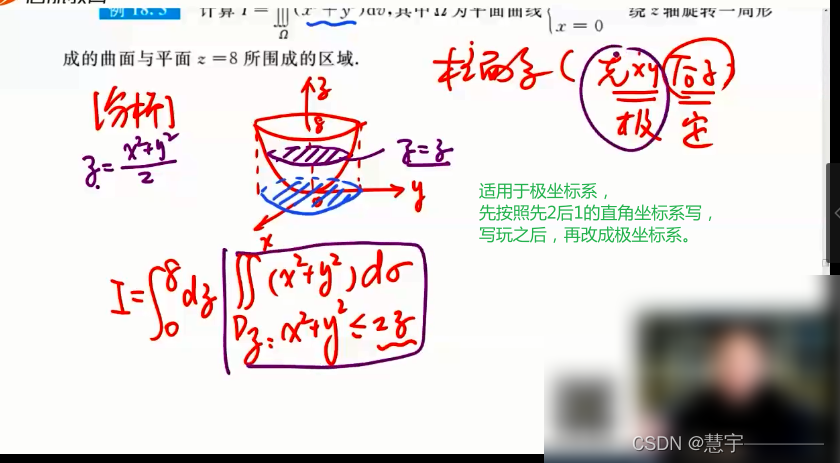
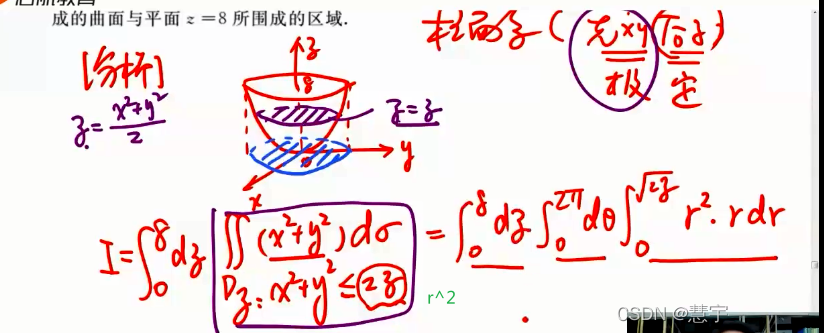
在这里插入图片描述

球面坐标系（知道积分过程，xyz dv 的表示方式）

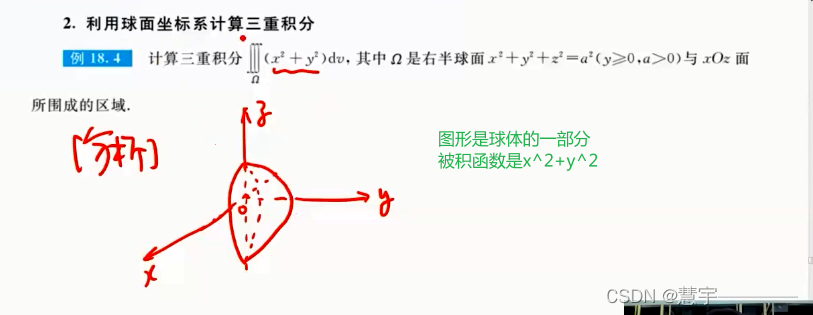
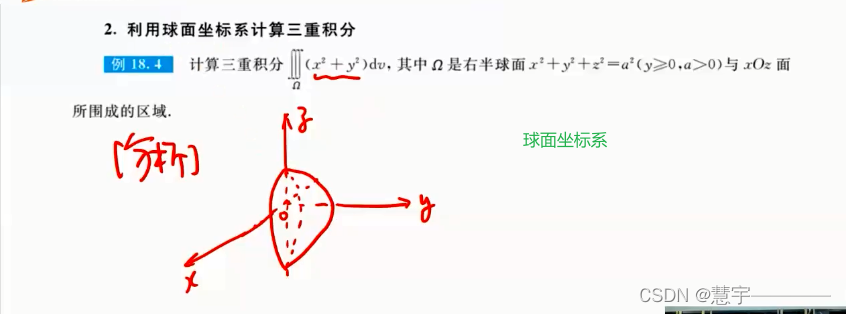
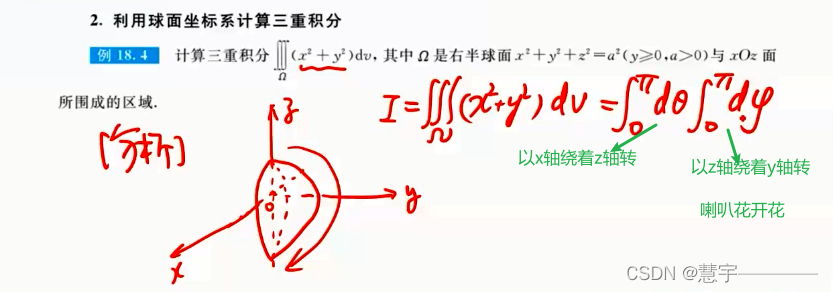
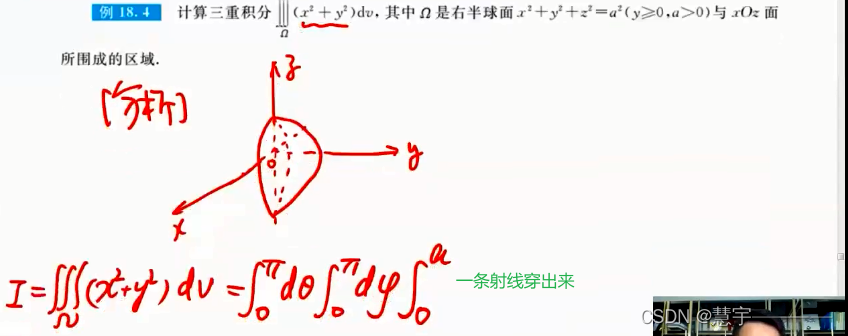
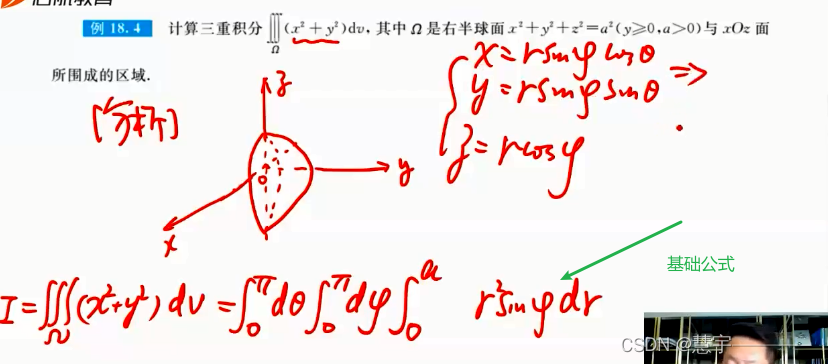
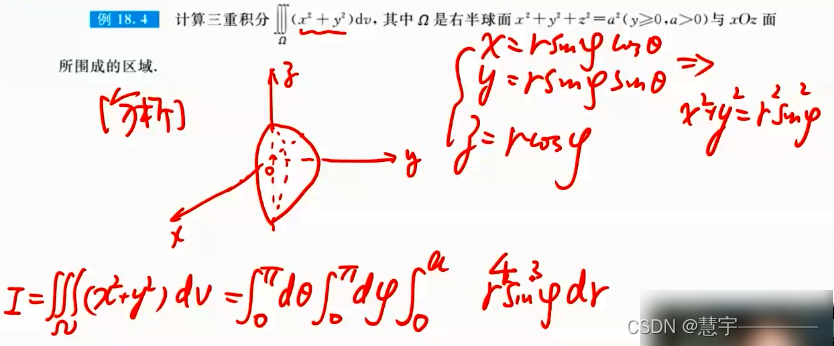
在这里插入图片描述

1.2.2技术方法

对称性

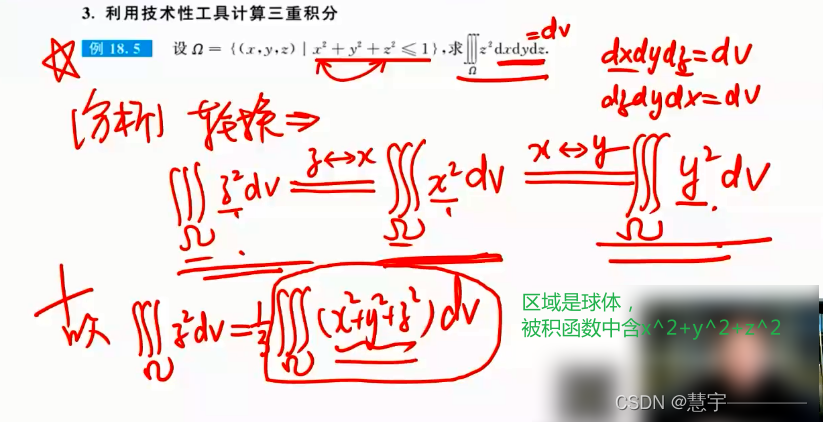
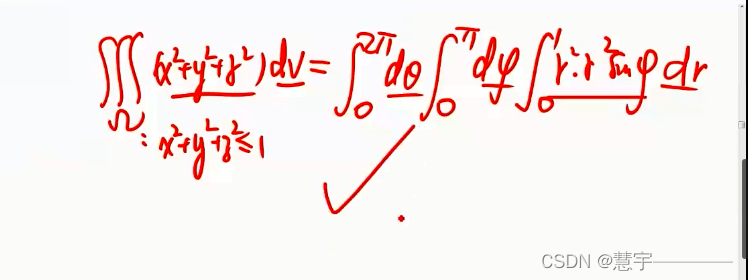
在这里插入图片描述

形心公式的逆用

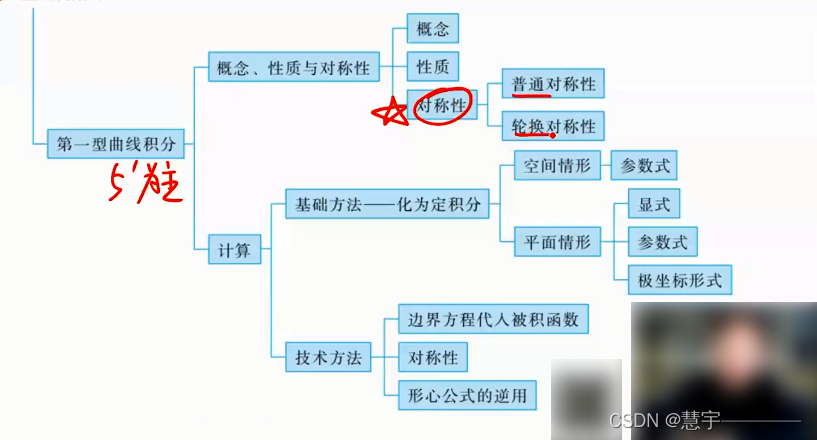
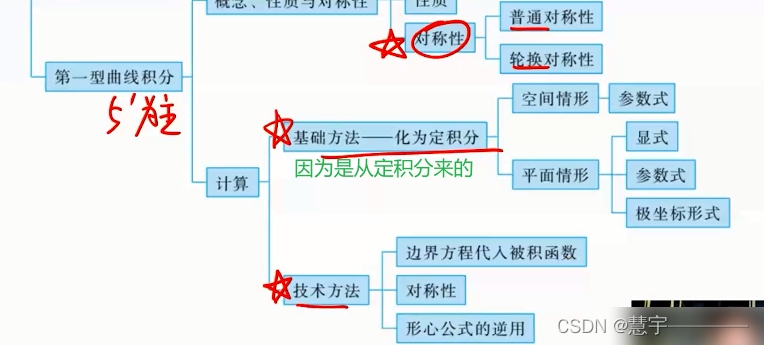
2、第一型曲线积分

2.1 概念性质与对称性

2.1.1 概念

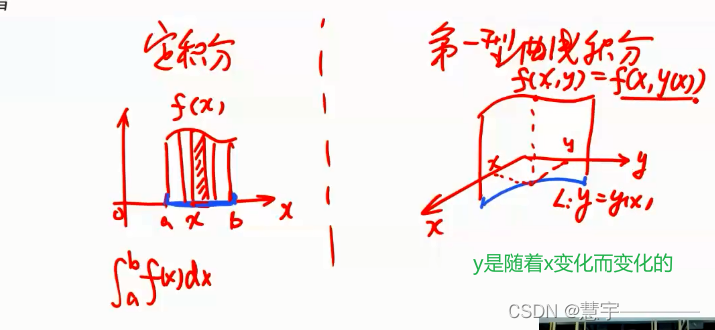
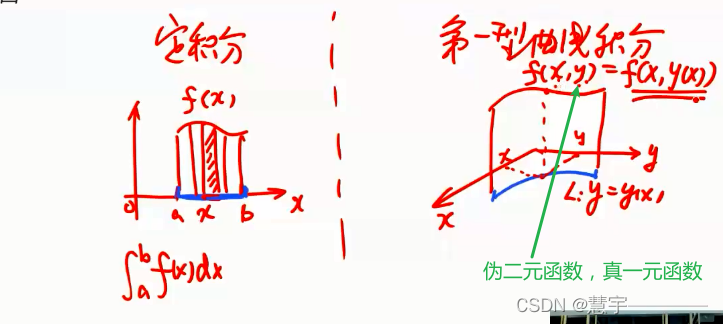
在这里插入图片描述

2.1.2 性质

在这里插入图片描述

2.1.3 对称性

普通对称性

轮换对称性

2.2 计算

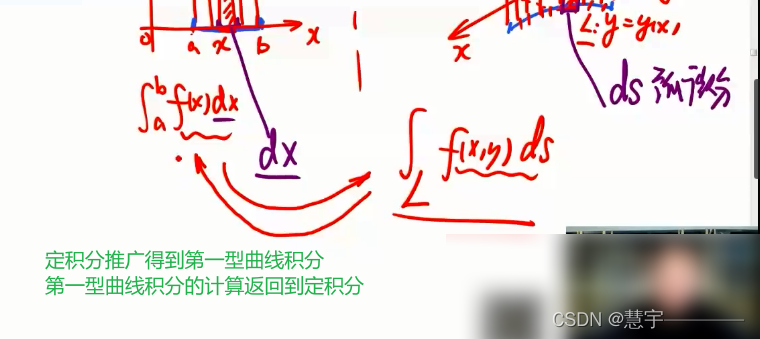
在这里插入图片描述

2.2.1基础方法（化为定积分）

在这里插入图片描述

平面情形

在这里插入图片描述

显式（数一数二专项的弧长积分中学习过）

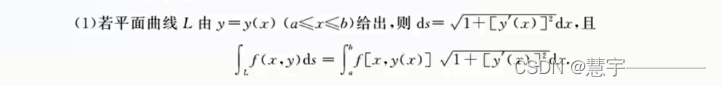
在这里插入图片描述

参数式

在这里插入图片描述

极坐标形式

在这里插入图片描述

空间情形

参数式

在这里插入图片描述

2.2.2 技术方法

边界方程代入被积函数

在这里插入图片描述

对称性

形心公式的逆用

普通对称性应用的习题

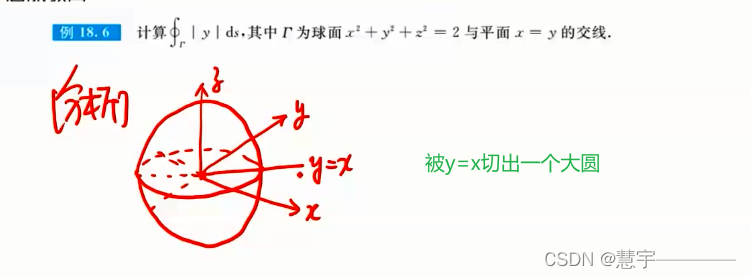
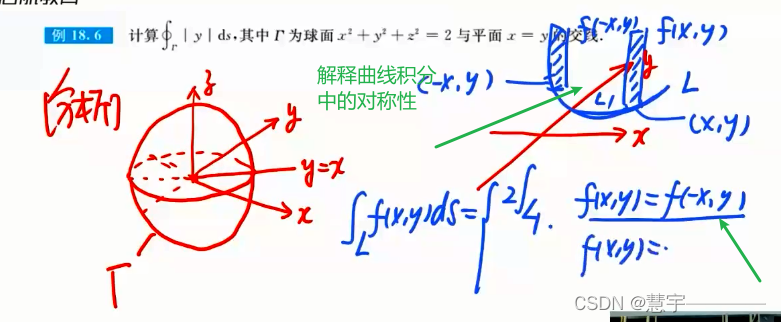
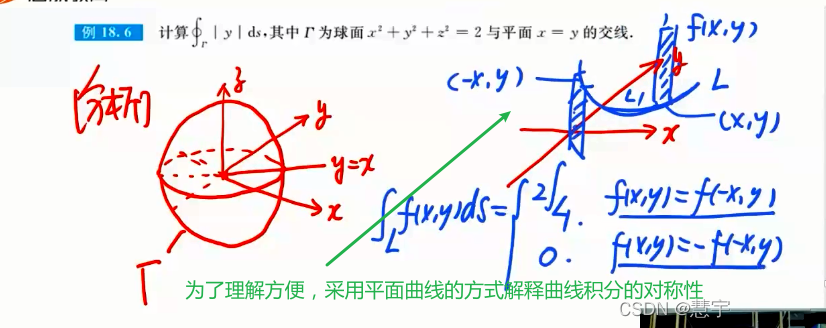
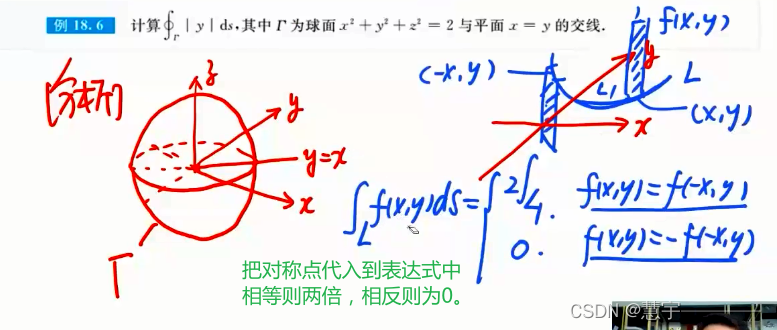
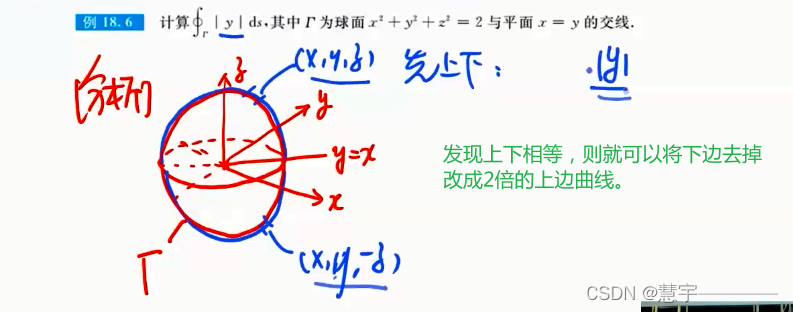
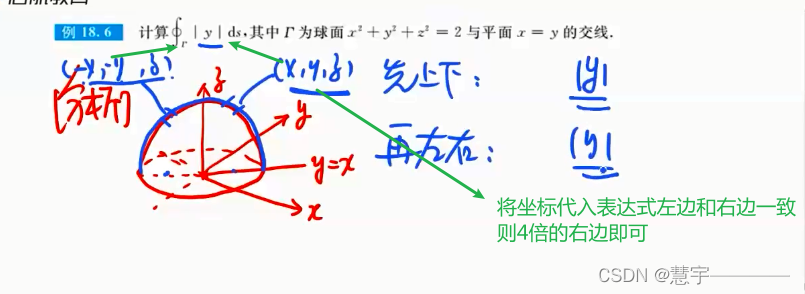
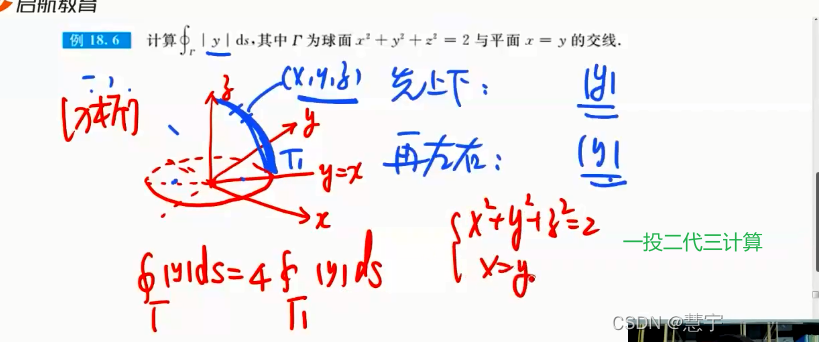
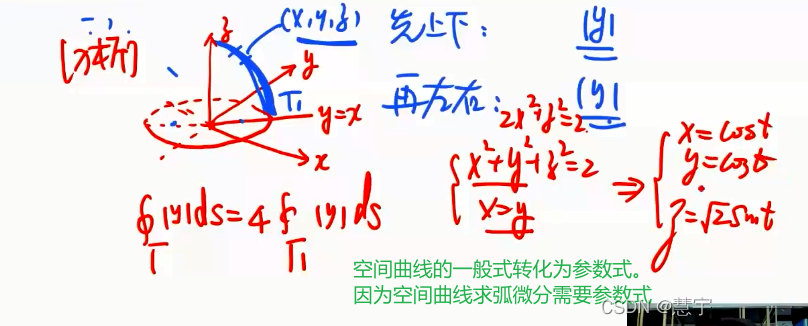
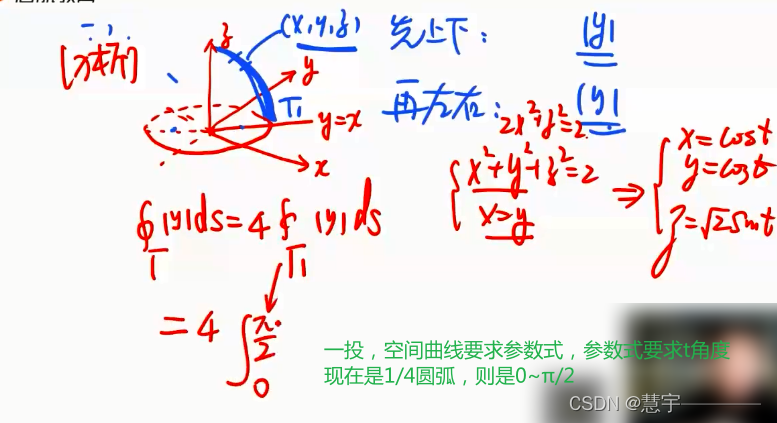
在这里插入图片描述

轮换对称性应用的习题

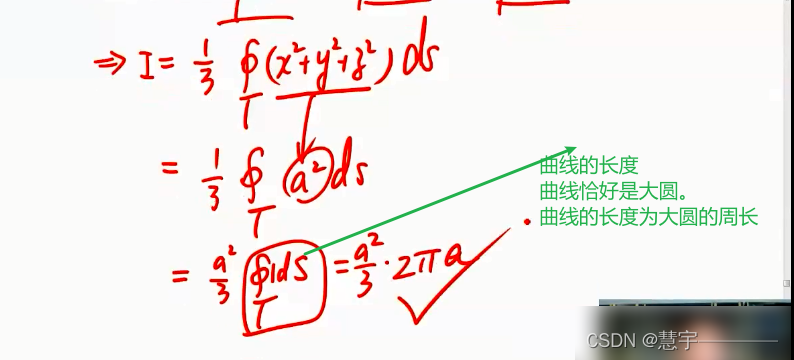
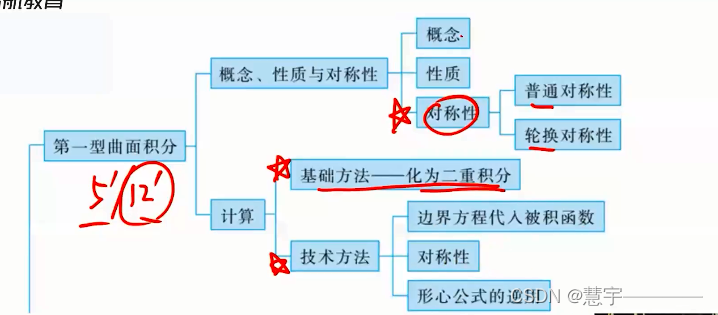
在这里插入图片描述

3、第一型曲面积分

3.1 概念性质与对称性

3.1.1 概念

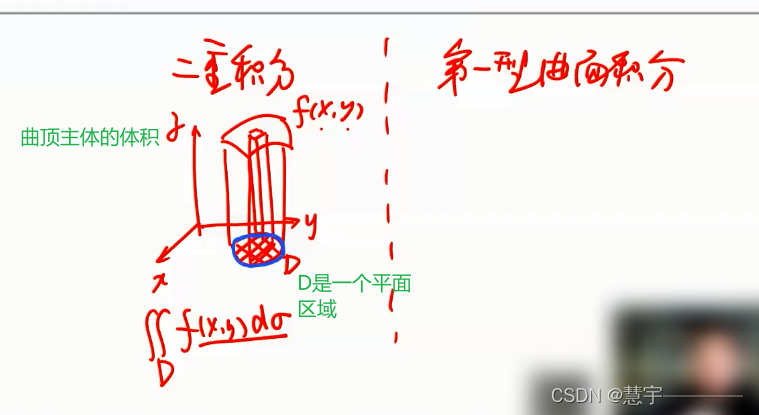
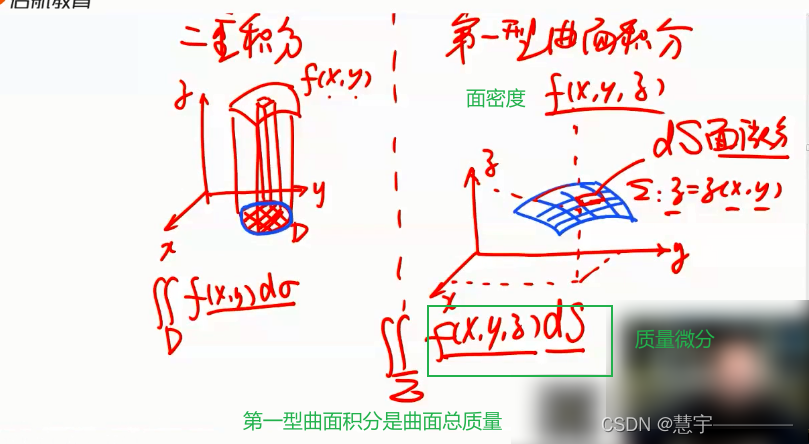
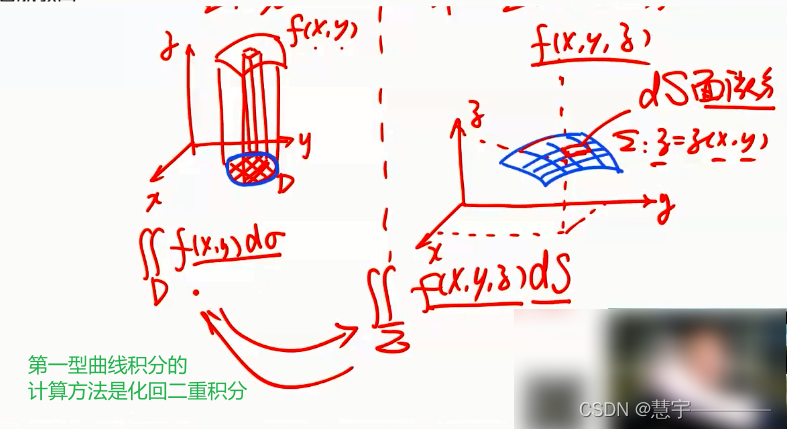
在这里插入图片描述

3.1.2 性质

在这里插入图片描述

3.1.3 对称性

普通对称性

轮换对称性

3.2 计算 (12/5)

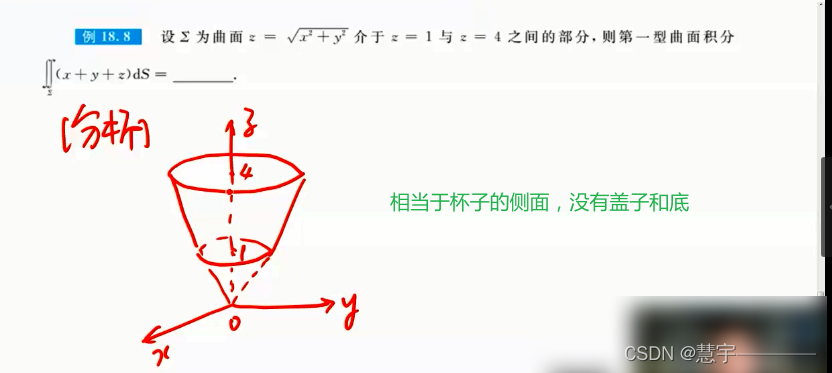
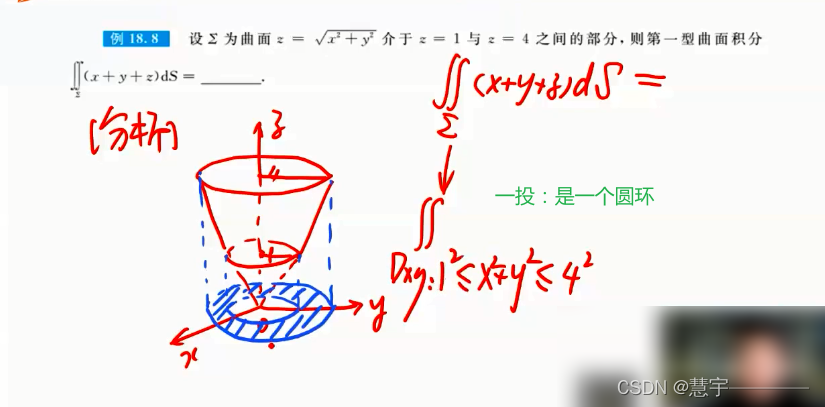
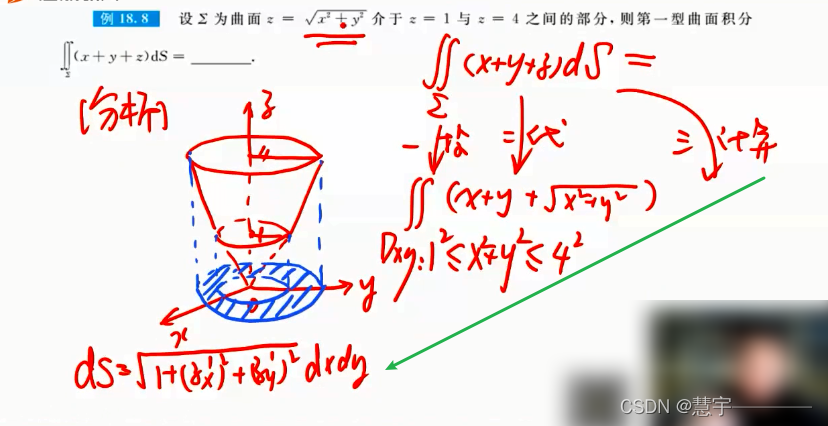
3.2.1基础方法（化为二重积分）

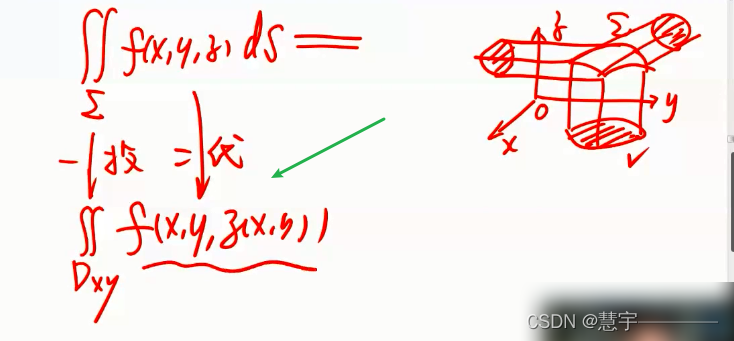
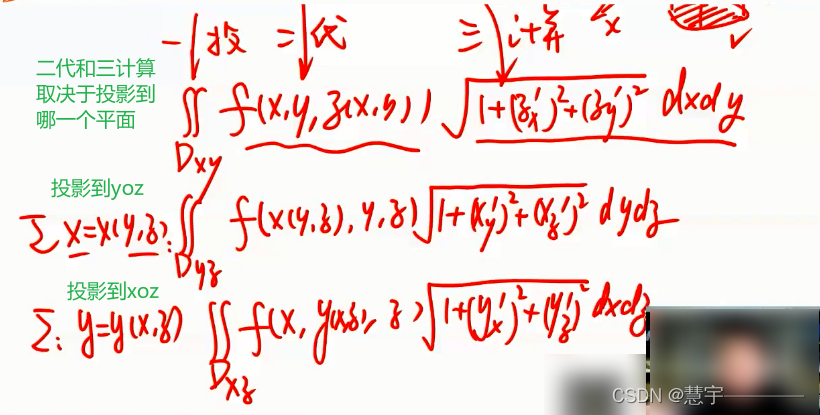
在这里插入图片描述

3.2.2 技术方法

边界方程代入被积函数

对称性

形心公式的逆用

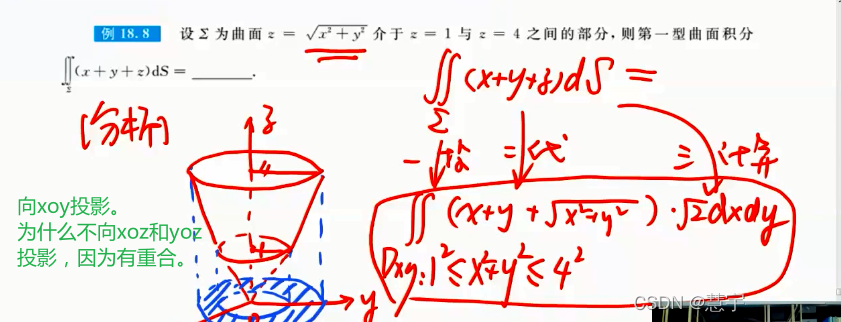
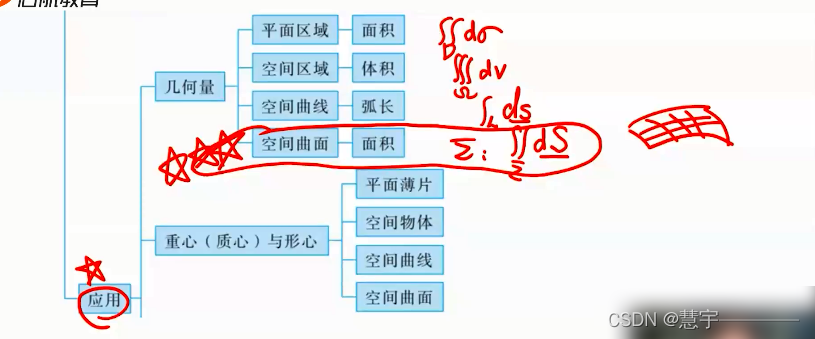
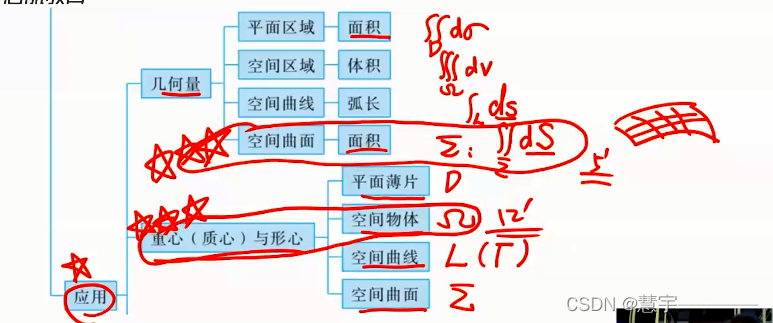
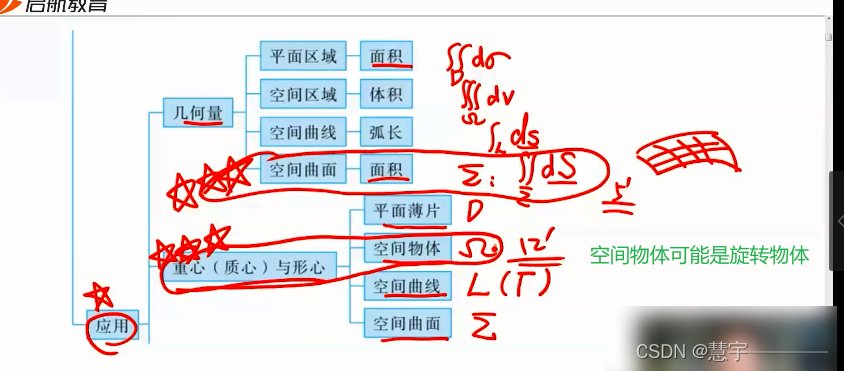
在这里插入图片描述

4、应用(二重积分三重积分曲线曲面积分)

在这里插入图片描述

4.1 几何量

平面区域(面积)

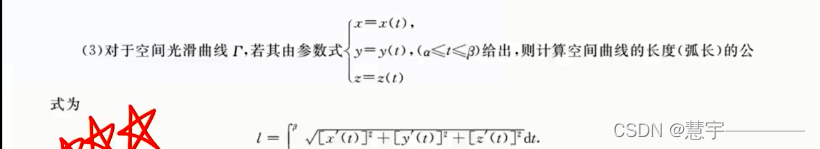
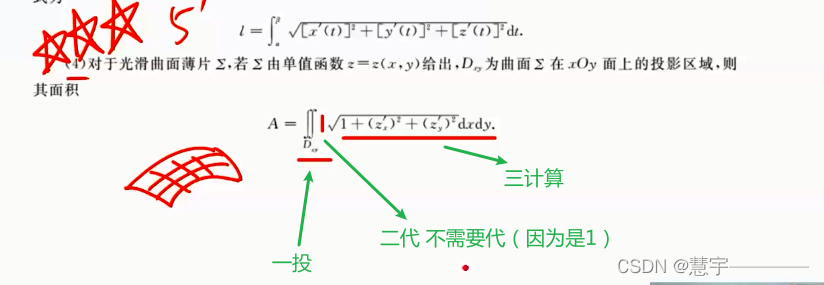
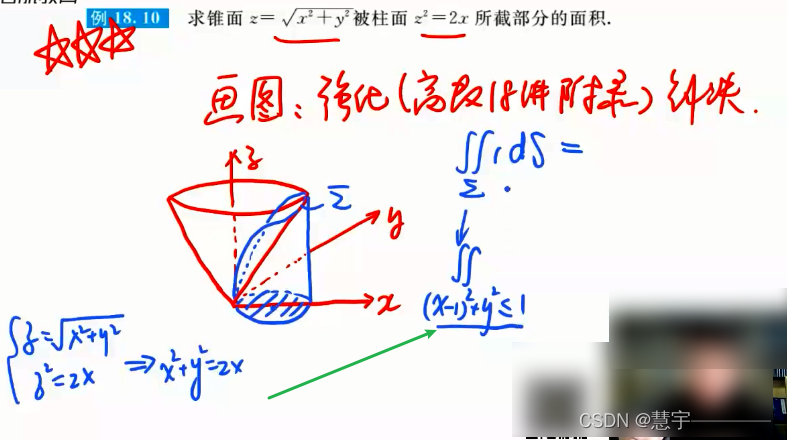
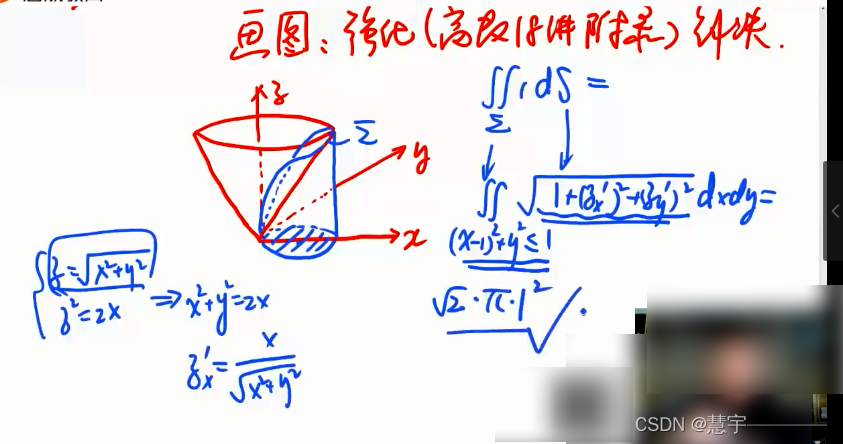
在这里插入图片描述

空间区域（体积）

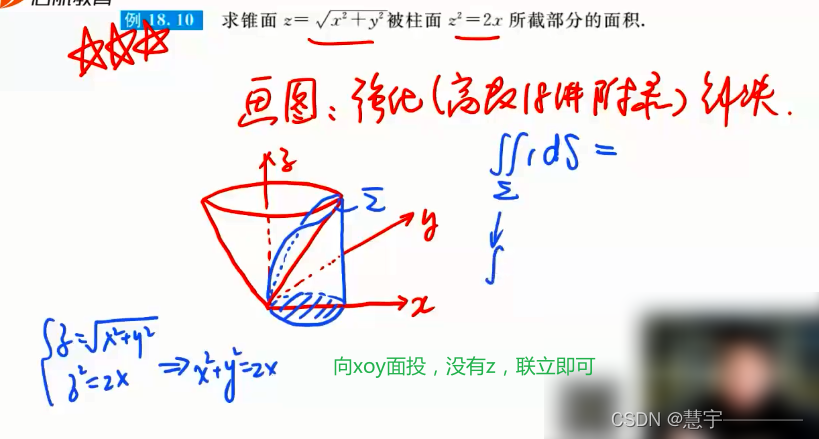
在这里插入图片描述

空间曲线（弧长）

在这里插入图片描述

空间曲面（面积）

在这里插入图片描述

4.2 重心（质心）与形心

平面薄面

空间物体质心

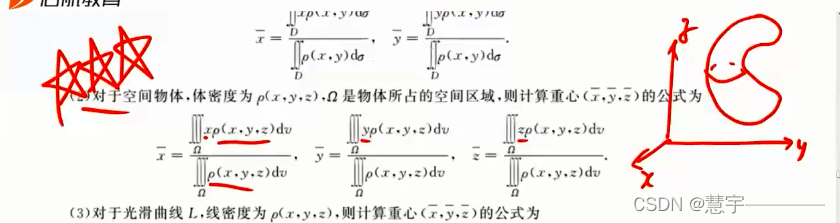
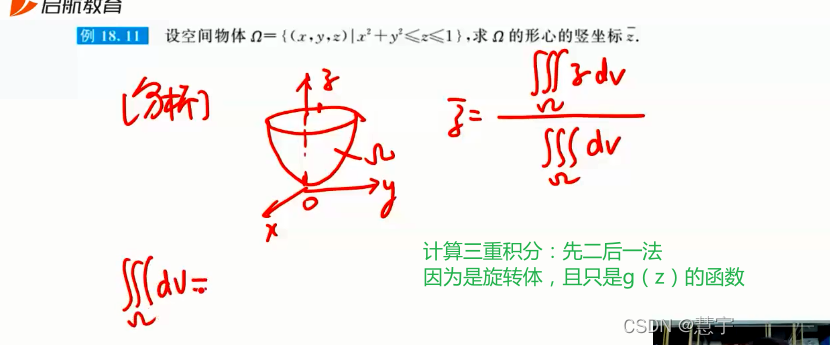
在这里插入图片描述

空间物体形心

在这里插入图片描述

空间曲线

空间曲面

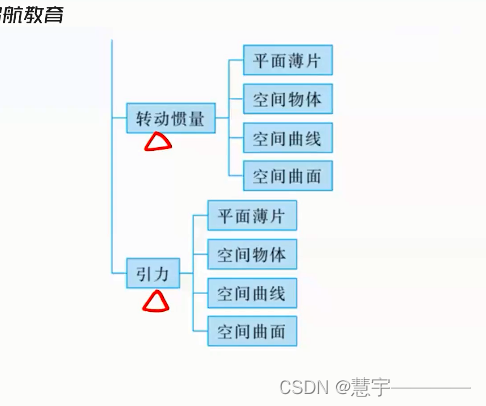
在这里插入图片描述

4.3 转动惯量

在这里插入图片描述

平面薄面

空间物体

在这里插入图片描述

空间曲线

空间曲面

4.4 引力

在这里插入图片描述

平面薄面

空间物体

在这里插入图片描述

空间曲线

空间曲面

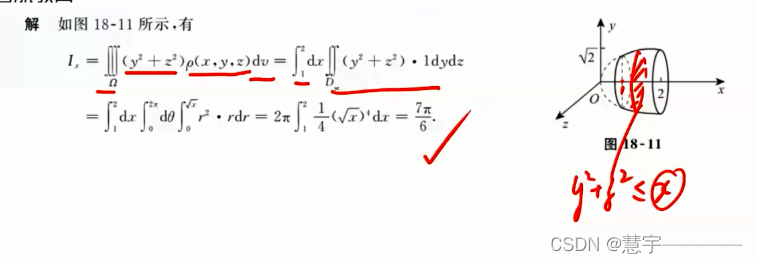
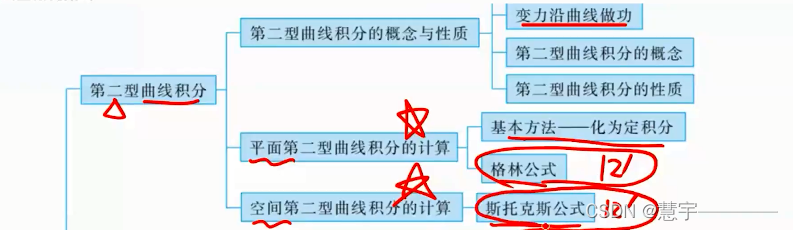
在这里插入图片描述

5、第二型曲线积分

在这里插入图片描述

5.1 概念与性质

场的概念

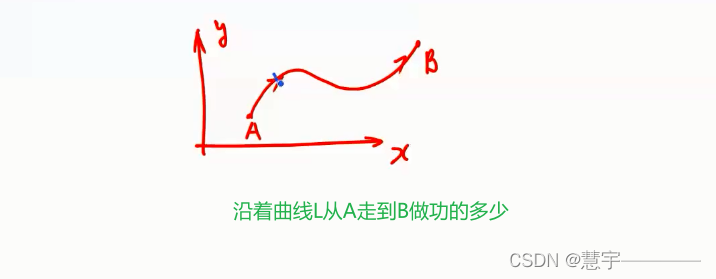
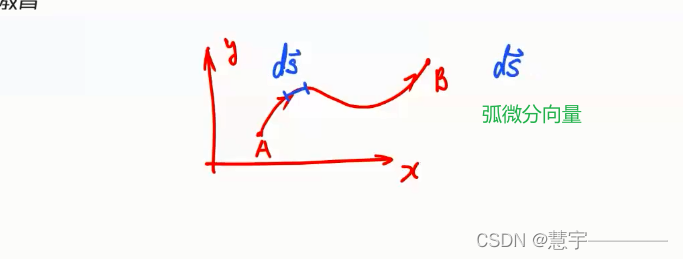
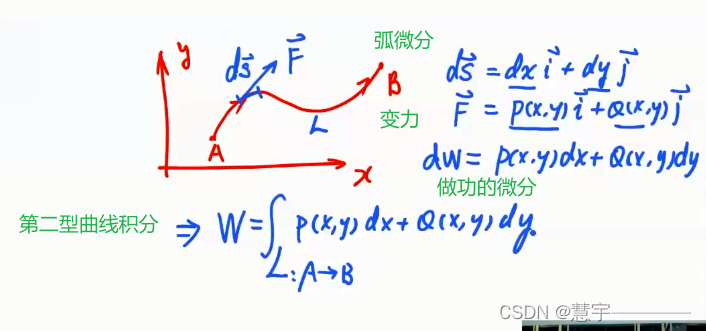
在这里插入图片描述

变力沿曲线做功

在这里插入图片描述

第二性曲线积分的概念

5.2 平面第二型曲线积分的计算

基本方法（化为定积分）

在这里插入图片描述
写成直角坐标系下的

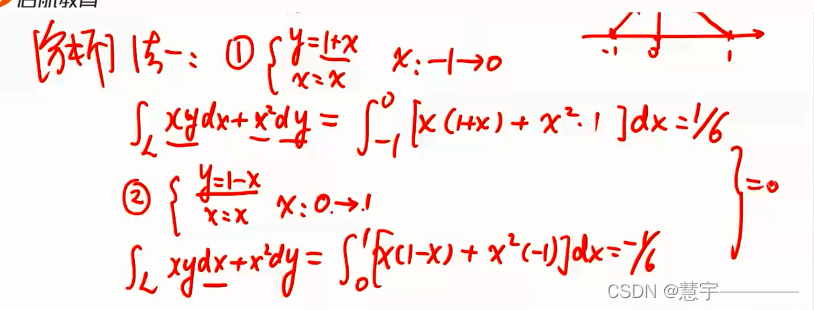
第二性曲线积分的性质

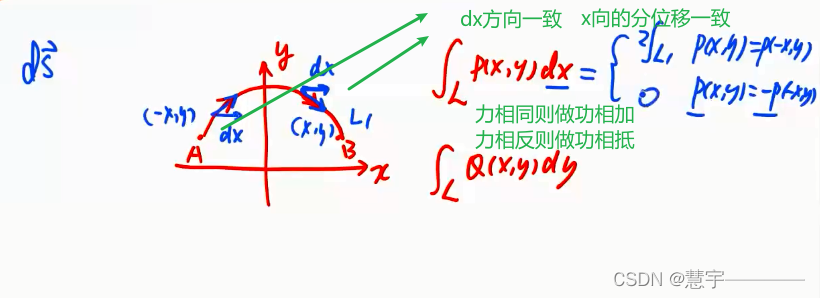
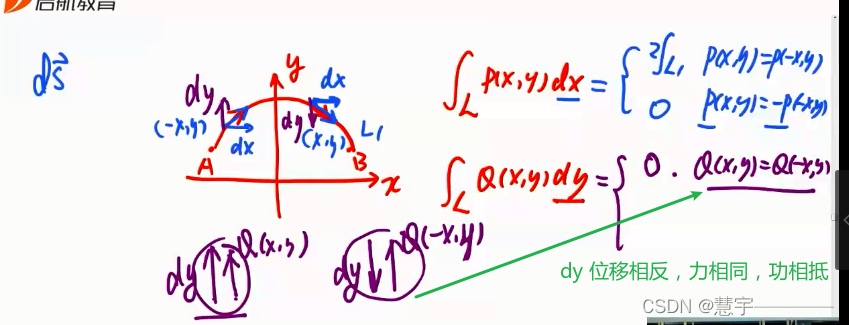
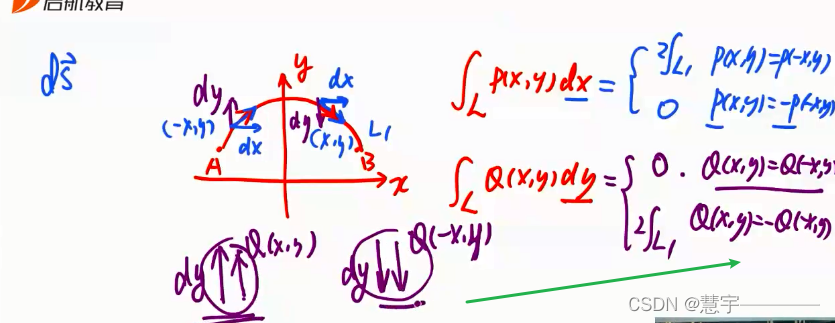
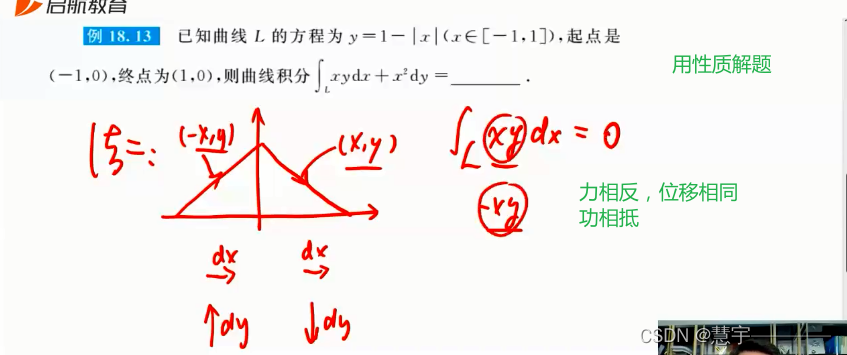
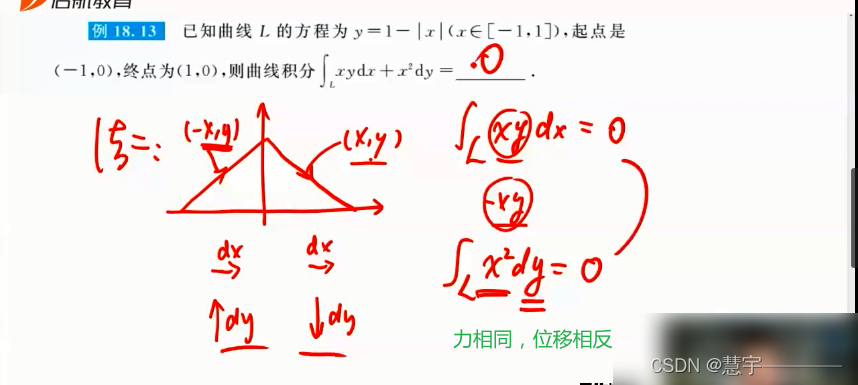
在这里插入图片描述

格林公式

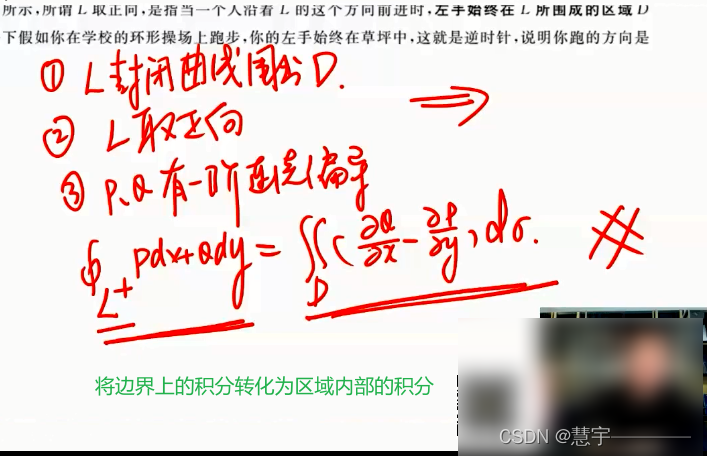
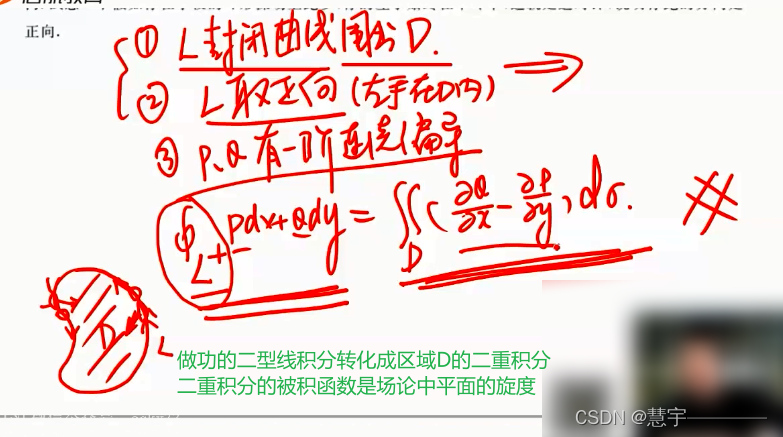
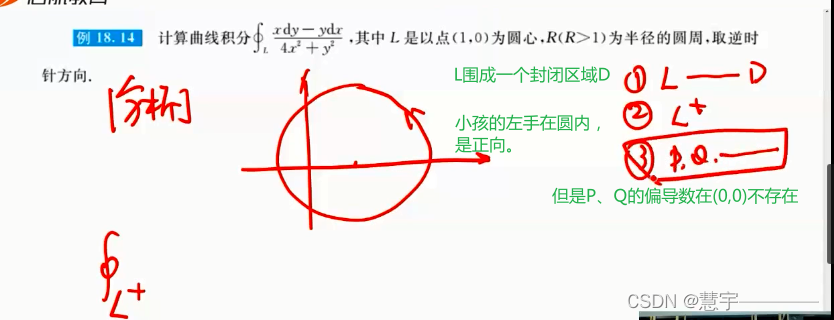
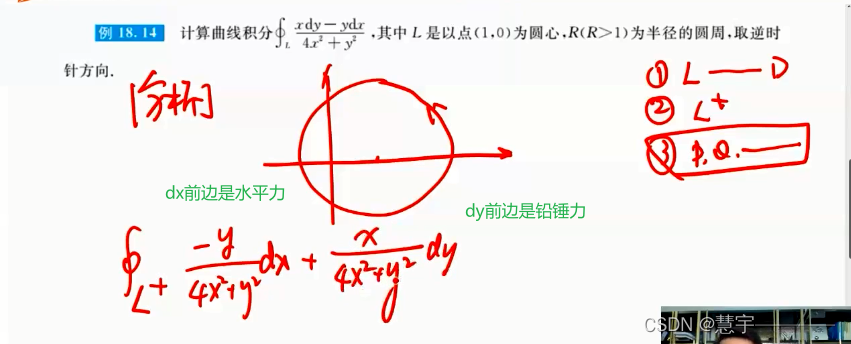
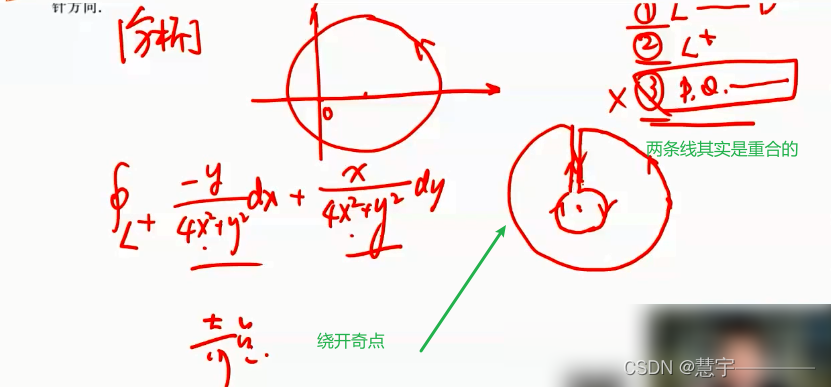
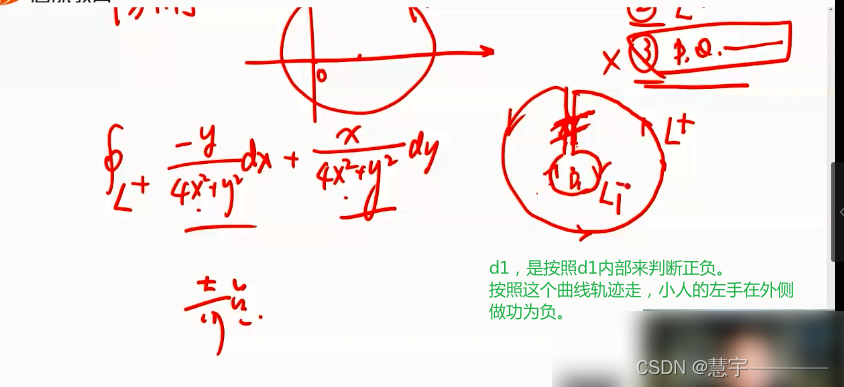
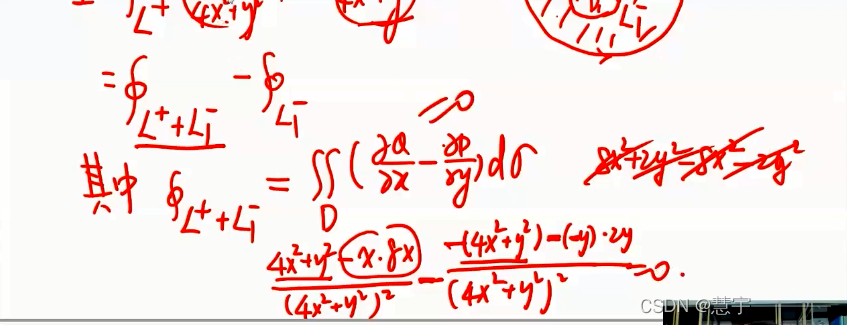
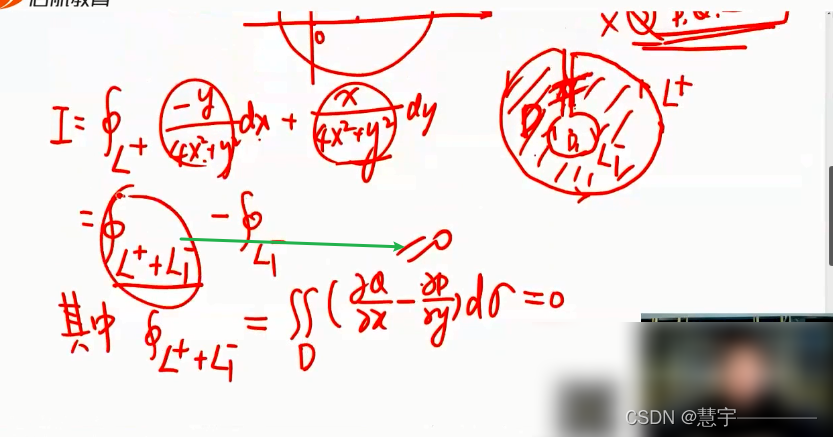
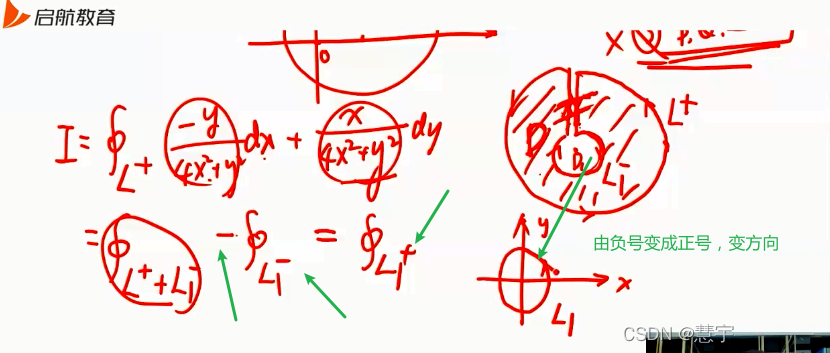
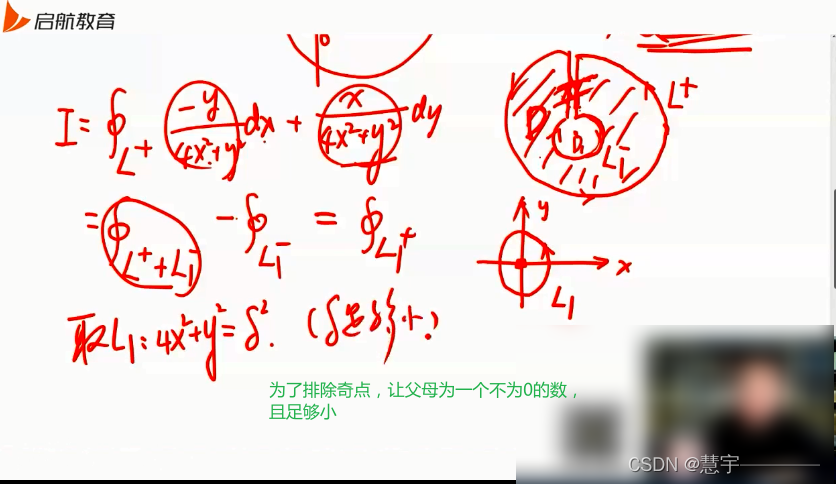
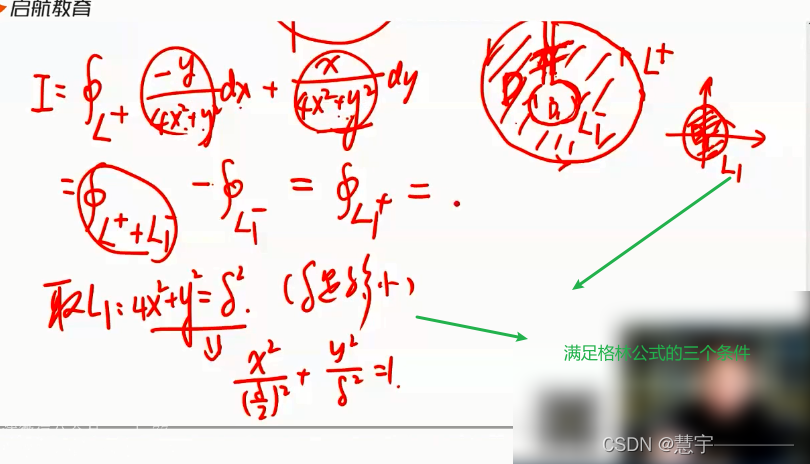
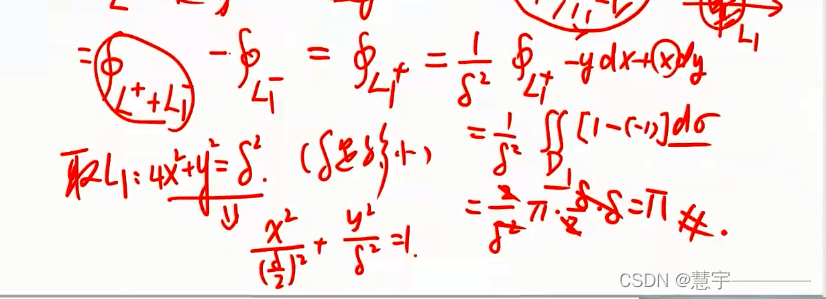
在这里插入图片描述

5.3 空间第二型曲线积分的计算

斯托克公式

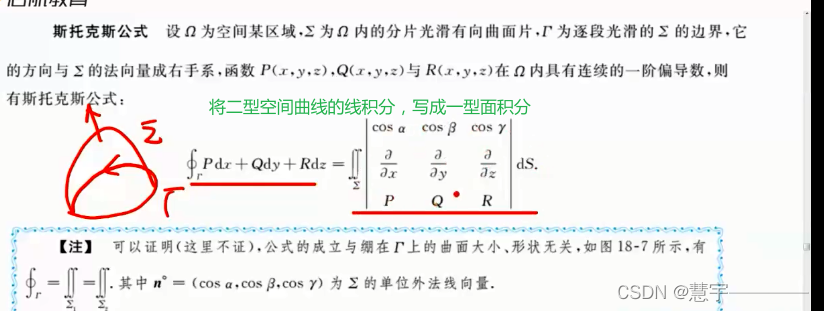
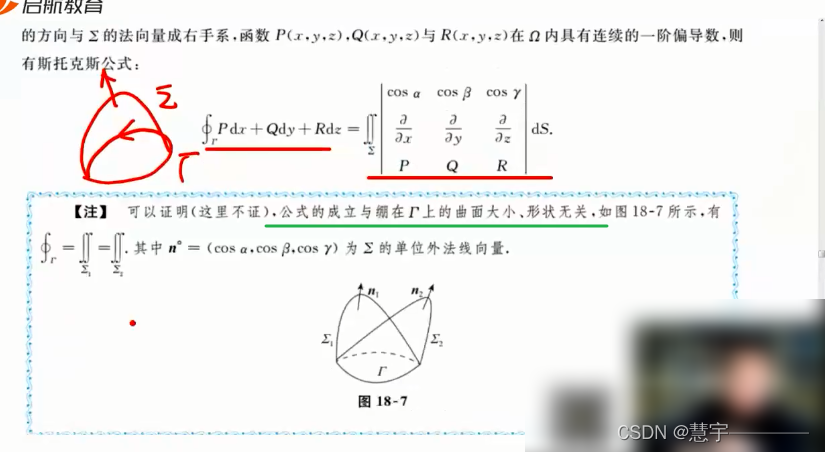
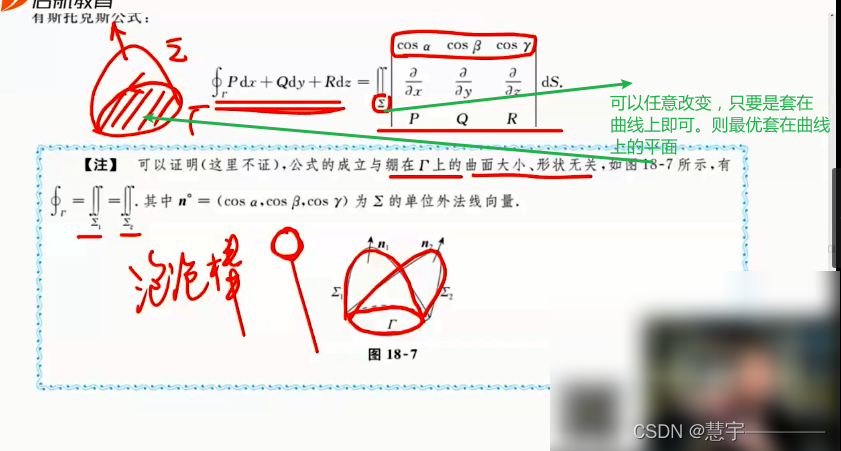
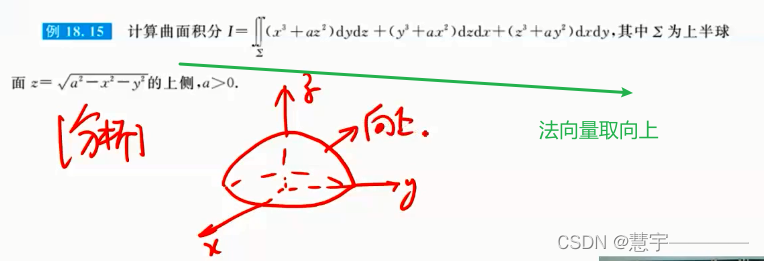
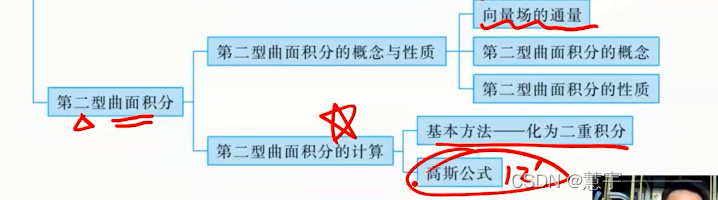
在这里插入图片描述

6、第二型曲面积分

6.1 概念与性质

向量场的通量

第二型曲面积分的概念

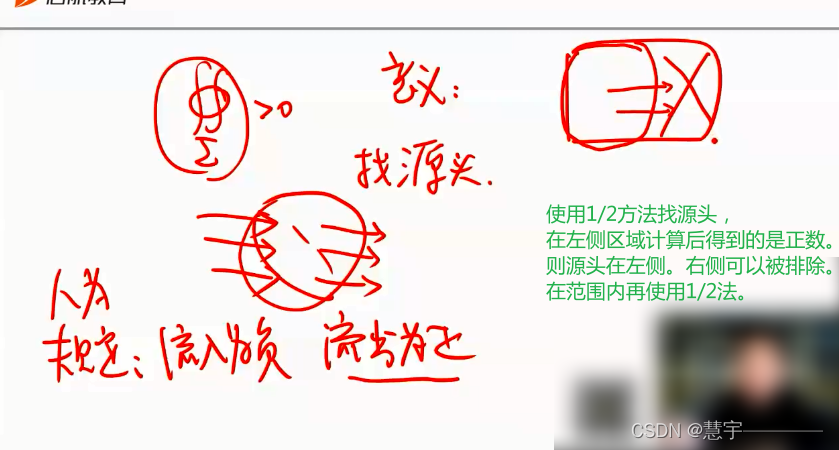
在这里插入图片描述

在这里插入图片描述

第二型曲面积分的性质

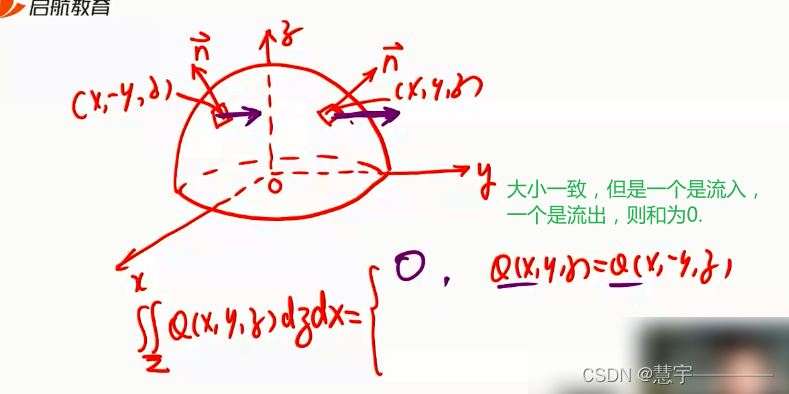
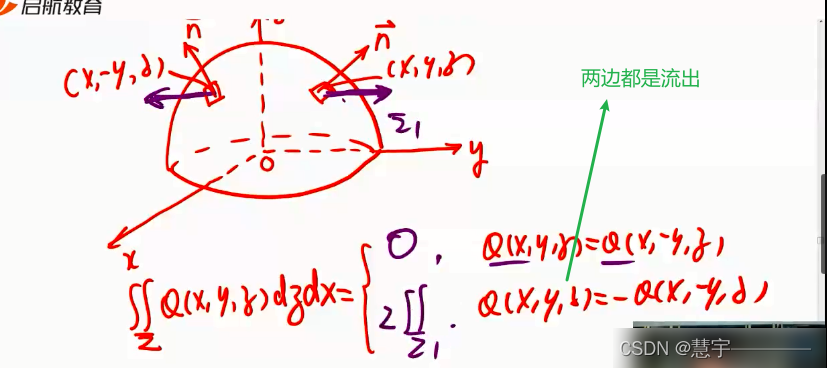
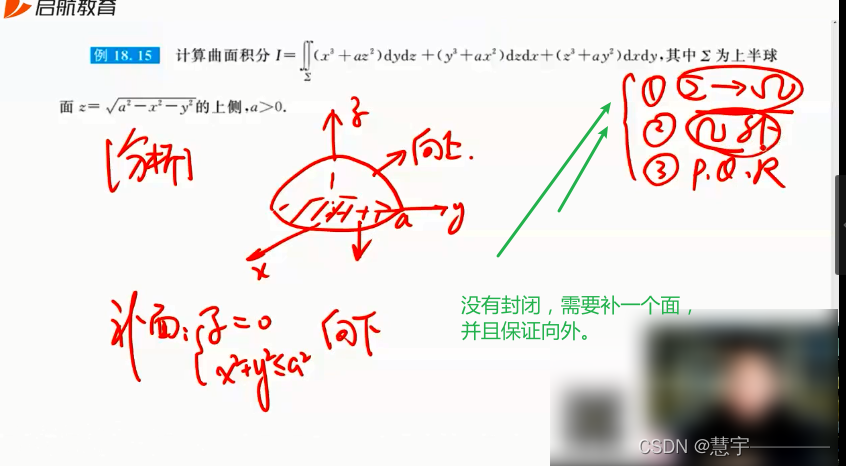
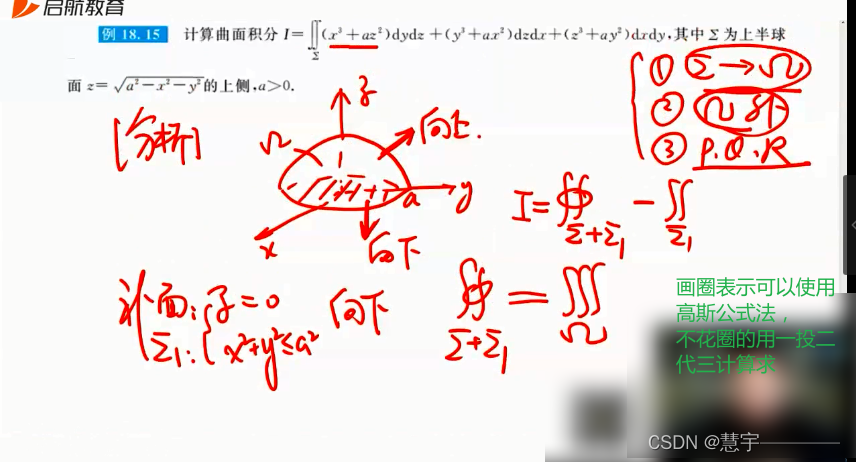
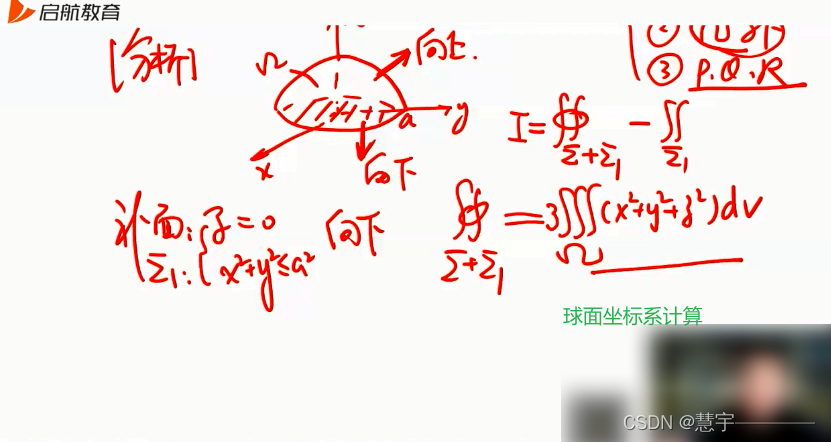
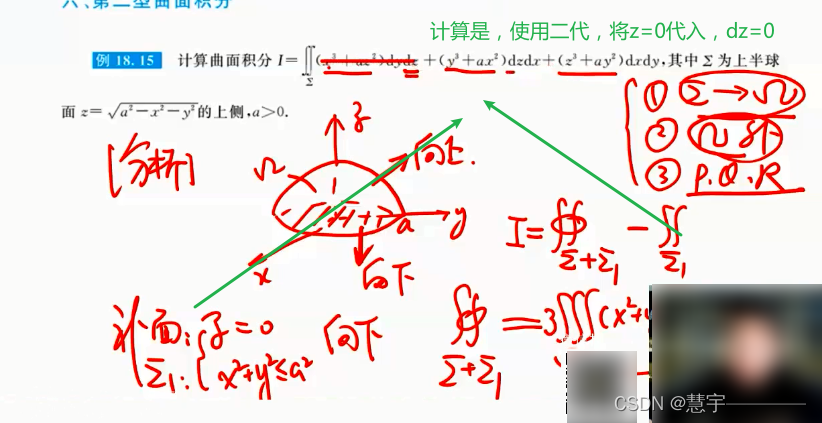
在这里插入图片描述

6.2 计算

基本方法（化为二重积分）

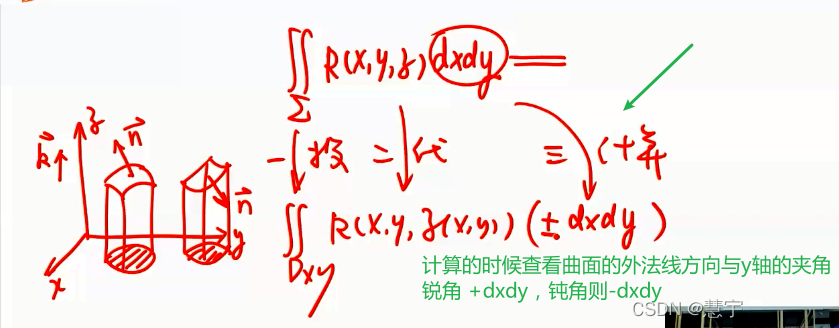
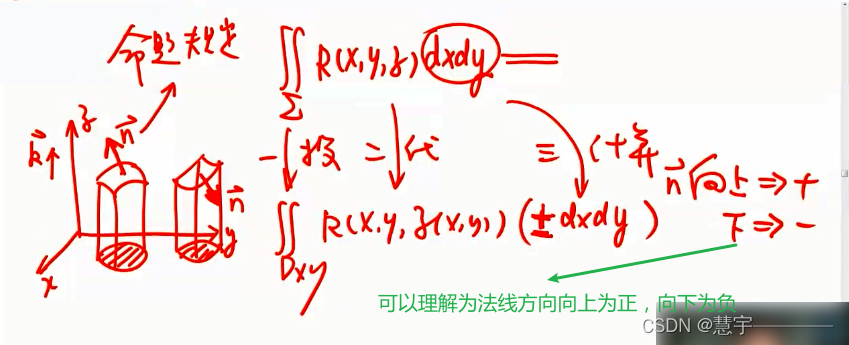
在这里插入图片描述

高斯公式

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

开发者涨薪指南

48位大咖的思考法则、工作方式、逻辑体系

数据结构与算法最新文章

【力扣106】从中序与后续遍历序列构造二叉

leetcode 322 零钱兑换

哈希的应用：海量数据处理

动态规划|最短Hamilton路径

华为机试_HJ41 称砝码【中等】【menset】【

【C与数据结构】——寒假提高每日练习Day1

基础算法——堆排序

2023王道数据结构线性表--单链表课后习题部

LeetCode 之反转链表的一部分

【题解】lintcode必刷50题＜有效的括号序列

上一篇文章下一篇文章查看所有文章

加:2022-06-06 17:30:41 更:2022-06-06 17:32:16

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

360图书馆购物三丰科技阅读网日历万年历 2025年2日历

-2025/2/6 5:54:20-

图片自动播放器
↓图片自动播放器↓

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

网站联系: qq:121756557 email:121756557@qq.com IT数码