(x,0)---m*n*k---(1,0)(0,1)
(x,8)---m*n*k---(1,0)(0,1)
用x和0分类,然后再用x和8分类,在同样收敛误差的情况下,是否因为8有两个圆而使得迭代次数是0的两倍?这个答案是否定的。
| 3 | 0 | 8 | 2 | 9 | 6 | 5 | 4 | 7 | |
| X:1 | 35671.24 | 23558.45 | 16861 | 11792.54 | 10721.14 | 10241.39 | 10137.68 | 9577.513 | 9568.94 |
| 3 | 4 | 9 | 7 | 1 | 6 | 0 | 8 | 5 | |
| 2 | 33389.61 | 19984.86 | 13772.15 | 12555.62 | 11792.54 | 9360.106 | 8358.603 | 7658.015 | 7100.643 |
| 1 | 2 | 9 | 7 | 8 | 4 | 0 | 5 | 6 | |
| 3 | 35671.24 | 33389.61 | 19919.65 | 17331.39 | 17015.68 | 15199.52 | 12572.23 | 11703.08 | 8136.266 |
| 2 | 9 | 3 | 0 | 1 | 6 | 7 | 8 | 5 | |
| 4 | 19984.86 | 18523.66 | 15199.52 | 11983.15 | 9577.513 | 9020.96 | 7572.704 | 6106.347 | 5689.266 |
| 3 | 1 | 7 | 2 | 9 | 8 | 4 | 0 | 6 | |
| 5 | 11703.08 | 10137.68 | 8617.161 | 7100.643 | 6794.688 | 6116.397 | 5689.266 | 5402.955 | 5362.608 |
| 0 | 1 | 2 | 9 | 4 | 7 | 8 | 3 | 5 | |
| 6 | 25605.5 | 10241.39 | 9360.106 | 9044.211 | 9020.96 | 8983.447 | 8626.678 | 8136.266 | 5362.608 |
| 9 | 3 | 2 | 1 | 6 | 5 | 0 | 4 | 8 | |
| 7 | 20211.46 | 17331.39 | 12555.62 | 9568.94 | 8983.447 | 8617.161 | 7822.01 | 7572.704 | 7073.432 |
| 0 | 3 | 1 | 6 | 2 | 7 | 9 | 5 | 4 | |
| 8 | 27905.07 | 17015.68 | 16861 | 8626.678 | 7658.015 | 7073.432 | 6966.322 | 6116.397 | 6106.347 |
| 7 | 3 | 4 | 2 | 0 | 1 | 6 | 8 | 5 | |
| 9 | 20211.46 | 19919.65 | 18523.66 | 13772.15 | 13346.79 | 10721.14 | 9044.211 | 6966.322 | 6794.688 |
让x分别等于1,2,3,4,5,6,7,9分别和0和8分类,得到的迭代次数没有任何的倍数关系, 如果考虑0的圆比8的圆大些,那大小关系总应该是一致的。但事实上大小关系也是不一致的,1,2,4,6,7,9的迭代次数8比0大。而3和5的迭代次数是0比8大。
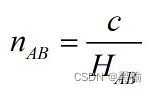
考虑迭代次数与熵成反比的假设,迭代次数越大表明两个被分类对象越像,熵越小。并且认为形态0是形态8的一个局部,这就意味着不能用x和0的迭代次数去估算x和8的迭代次数,表明局部的形态差异和整体的形态差异之间并不存在一种简单的加和关系。局部差异和整体差异之间的关系取决于分类环境x,x不同这二者的关系可能都不同。
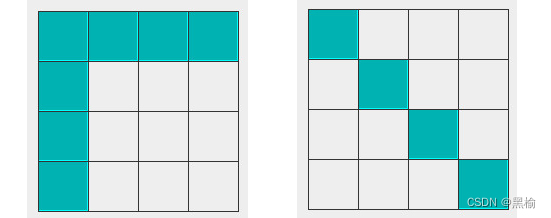
这是一组4*4的图片
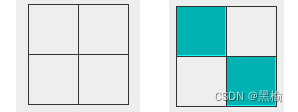
这是一组2*2的图片。把2*2的图片看作4*4的图片的局部,显然是很难用2*2的图片差异去预知4*4的图片差异。
像盲人摸象一样,在形态的世界我们不能简单的由局部去推及整体,但物质世界并不都是如此。比如2-1=1,同样102-101=1,1到10的加法律和100-110的加法律是一样的,对于整个数轴都成立。这就意味这只要了解1-10这个10个数的作用关系就可以由此推及整体,在数的领域由局部推及整体是可能的。这种规律没有局部和整体的差别。
或者比如氢原子的光谱在地球上和在系外星系的氢光谱是一样的,没有差别。地球上的物理定律和宇宙某个角落的物理定律也应该是一样的。可以用地球上的物理实验去预知宇宙某个角落的现象。所以对于物理定律而言也没有局部和整体的差别。
尽管能量有一个最小单位,但因为非常小对于宏观物体而言假设能量是连续的,而把原子当作一维实数连续性的一个物质体现。因此物理定律有一种严格的数学表达,所以无论对于物质还是实数都可以由局部去推及整体。这种可以由局部去推及整体的分类方法是一种元素的分类法。因为粒子之间的相对位置关系并不影响分类,因此是一种一维的连续的内在递进的分类法。
现在由一个沙漏从高处向下漏沙子,当沙子比较少的情况下,可以不考虑形态特征,可以用元素分类法去近似。可以明确的由局部去预知整体的行为。但当沙子比较多的时候,这时这堆沙子的行为变得不可测,其整体特征变得与局部特征很不相同。所以这个过渡可以解释为当沙子比较多的时候,其形态特征变得不再可被忽略,这时应该考虑的是形态的整体的差异,而不是其组成部分。其整体的形态差异已经无法用局部的特征去预知。
所以有理由认为涌现行为可以用形态分类法去解释,这是一种考虑粒子相对位置关系的二维的非递进的,承认整体和局部差异的分类法。这种分类法相当于认为每个形态都是不可分的, 只能当作一个整体来看待,每个分类行为都是一个原子行为。而涌现的奇特现象就是形态内在非递进现象的一种体现。
