1.概述
?泊松分布源于泊松过程,与指数分布,伽马分布有着紧密的联系,本文在参考相关资料的基础上,进行详细推导以加深理解。
2.推导与理解
2.1直观对比
? 泊松分布可以由二项分布推导得到!二项分布与泊松分布的pdf分别如下:
? ? ? ??????????????????? ? ? ? ? ? ? ? ? (1)
? ? ? ??????????????????????????? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(2)
直观的来看二项分布和泊松分布似乎无关。但仔细观察会发现一种非常有趣的关系。泊松分布只是二项分布的一个特例——即试验的数量足够大,从而给定的成功概率?就很小。当
趋于无穷大且
接近零时,二项分布就接近泊松分布。
2.2 详细推导
当我们有固定数量的事件 时,每个事件的成功概率
?都是恒定的,此时上述二项分布有效。
想象一下,假定我们不知道会进行多少次试验。相反,我们只知道每个时间段的平均成功次数。也就是说比如我们知道每天事件的成功率,但不知道导出该比率的试验次数 或成功概率
。
定义一个数字
让它表示每天的成功率(特定时间的成功次数)。用试验次数 (无论有多少次)乘以每次试验的成功概率
?。
可以这样想:如果成功的机会是 ? 并且我们每天运行
? 次试验,我们将观察到平均每天
次成功。这是我们观察到的成功率
?(平均成功次数)。
再看一次二项分布如下所示:
????????????????????????????????? ??
如上所述,当我们定义如下时:
????????????????????????????????????????????????????????????????????????
求解 ,我们得到:
????????????????????????????????????????????????????????????????????????
我们用这个表达式代替 ? 到上面的二项分布中,并在
趋于无穷时取其极限,即
????????????????
取出常数
和
并将右边 n-k??次方的项分解为 n 次方的项和 -k 次方的项,我们得到
????????????????????????????????
现在让我们取右边第一项的极限。我们可以分为三步进行。第一步是找到极限
???????????????????????????????????????????????? ? ??
在上式中,我们可以将分子与分母中的阶乘分别展开得到
???????????????????????????????
这样写,很明显,分子和分母的许多项抵消了,最终得到以下结果:
??????????????????????????????? ????????
由于我们抵消了 项,这里的分子剩下 k 项,从 n 到 n-k+1。而在分母中也有
项,因为有
的?
次幂。
然后展开分子与分母,我们可以将其重写为:
????????????????????????????????????????
这有 k 项。显然,当 接近无穷大时,这些
项中的每一项都接近 1。所以我们知道这一步的求解最终简化为一个1。这样我们就完成了第一步。
第二步是找到极限表达式中间项的极限,即
????????????????????????????????????????????????????????
???????????????????????????????????????????????????????????????
我们的目标是找到一种方法来操纵我们的表达式,使其看起来更像 e? 的定义,因为我们知道它的极限。首先可以定义一个变量?x 为
????????????????????????????????????????????????????????????????
现在让我们将其代入上述表达式,并采用如下变换:
????????????????????????????????????????
这个第二项最终简化得到?。这样我们就完成了第二步。只剩下最后第三步。我们的第三步也就是最后一步是找到右边最后一项的极限,即
????????????????????????????????????????????????????????
这很简单。当? ?接近无穷大时,此项变为
,等于 1。这样将这三个结果放在一起,我们可以将原来的极限改写为
???????????????????????
也就是:
??????????????????????????????????? ??
这就是广泛熟悉的泊松分布概率质量函数pmf,给出了给定参数??的每个周期成功
次的概率。
所以我们就证明了泊松分布只是二项分布的一个特例,其中 n 次试验的数量增长到无穷大,并且任何一次试验的成功概率都接近于零。泊松分布与二项分布的pdf曲线对比如下。
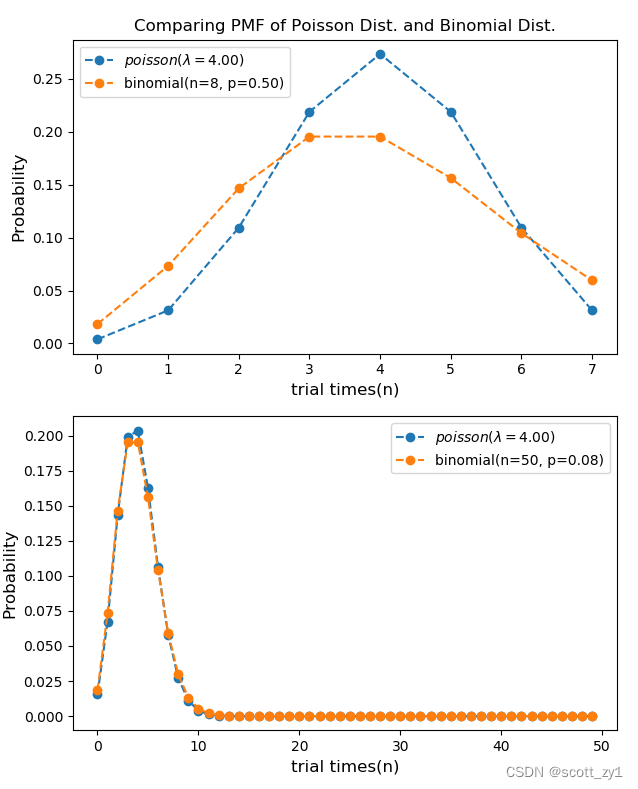
import numpy as np
from matplotlib import pyplot as plt
import operator as op
from functools import reduce
def const(n, r):
r = min(r, n-r)
numer = reduce(op.mul, range(n, n-r, -1), 1)
denom = reduce(op.mul, range(1, r+1), 1)
return numer / denom
def binomial(n, p):
q = 1 - p
#y = [const(n, k) * (p ** k) * (q ** (n-k)) for k in range(n)]
xlist = []
ylist = []
for k in range(n):
x = k
y = const(n, k) * (p ** k) * (q ** (n-k))
xlist.append(x)
ylist.append(y)
return xlist, ylist, np.mean(ylist), np.std(ylist)
def poisson(x, lamb):
xlist = []
ylist = []
for k in range(x):
xlist.append(k)
numer = np.exp(-lamb)*(lamb**k)
denom = reduce(op.mul, range(1, int(k+1)), 1)
y = numer/denom
ylist.append(y)
return xlist, ylist, np.mean(ylist), np.std(ylist)
fig,axes = plt.subplots(2,1, figsize=(6,9)) #get 1x1 subplots
axes[0].set_xlabel("trial times(n)", fontsize="12") #set the coordinate axis-x label
axes[0].set_ylabel("Probability", fontsize="12") #set the coordinate axis-y label
axes[0].set_title(u"Comparing PMF of Poisson Dist. and Binomial Dist.",fontsize=12)
axes[1].set_xlabel("trial times(n)", fontsize="12") #set the coordinate axis-x label
axes[1].set_ylabel("Probability", fontsize="12") #set the coordinate axis-y label
for idx, ls in enumerate([(4, 8),(4,50)]):
lamb, n = ls[0], ls[1]
p = lamb/n
xb, yb, _, _ = binomial(n, p)
x, y, _, _ = poisson(n, lamb=lamb)
axes[idx].plot(xb, yb, '--o', label=r'$poisson(\lambda=%.2f)$' % (lamb))
axes[idx].plot(x, y, '--o', label=r'binomial(n=%d, p=%.2f)' % (n, p))
axes[idx].legend()
axes[idx].legend()
#plt.savefig('./graph/binomial-poisson.png')