有人考试靠实力,有人考试靠视力,还有人考试靠想象力。
祝各位期末考试顺利~
考试时间:仨小时。
选择填空题共15道,每道1分。
第一道编程题15分,第二道编程题10分,第三道编程题10分。
共50分。
选择题 (总分:11.00)
1.?? ?若用一个大小为6的数组来实现循环队列,且当前rear和front的值分别为0和3,当从队列中出队一个元素,再入队两个元素后,rear和front的值分别为 __________ 。
A. 1和5 ? ?B. 2和4 ? ? ?C. 4和2 ? ? ?D. 5和1
正确答案: B
2.?? ?若已知一个栈的入栈序列是1、2、3、…、n-1、n,其输出序列为p1、p2、p3、…、pn,若p1=n,则pi为__________
A. i?? ? B. n-i?? ?C. n-i+1?? ? D.不确定
正确答案: C
3.?? ?已知二叉树的中序序列为:BADCE,后序序列为:BDECA,则其前序序列为:__________
A. ADBEC ? ? ?B. DECAB ? ? ?C. DEBAC ? ? D. ABCDE
正确答案: D
4.?? ?下列说法中,错误的是__________。
A. 无向图的邻接矩阵一定是一个对称矩阵。
B. 若有向图采用邻接表的存储方式,则其第i个链表中边结点个数是第i个顶点的出度。
C. 包含具有n个顶点的连通图G的全部n个顶点,仅包含其n-1条边的极小连通子图称为G的一个生成树。
D. 对于给定的带权连通无向图,从某源点到图中各顶点的最短路径构成的生成树一定是该图的最小生成树。
正确答案: D
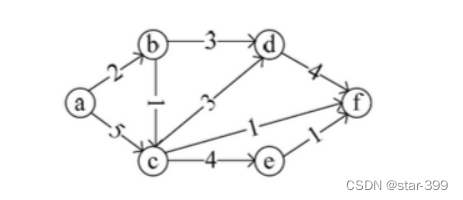
5.?? ?有向带权图,若采用迪杰斯特拉(Dijkstra)算法求源点a到其他各顶点的最短路径,得到的第一条最短路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是__________。
?
A ?.d,e,f ? ? ? B. ?e,d,f ? ? ?C. ? f,d,e ? ? ? ? D. ? f,e,d
正确答案: C
6.?? ?在建立散列表时,若散列函数为H(k),a与b分别为关键字值,则当__________ 时,称此现象为散列冲突。
A.a==b ? ? ? ?
B.a!=b ? ?
C.a==b且H(a)==H(b) ? ? ? ?
D.a!=b且H(a)==H(b)
正确答案: D
7.?? ?若在有序序列中采用折半查找方法进行查找,用来描述该查找过程的“判定树”的形状与__________有关。
A.序列中元素的值
B.序列中元素的排列次序
C.序列中元素的类型
D.序列中元素的个数
正确答案: D
8.?? ?下列排序方法中,不稳定的排序方法是__________。
A.冒泡排序 ? ? ?B. 快速排序 ? ? ? C.归并排序 ? ? ?D. 直接插入排序
正确答案: B
9.?? ?表达式a*(b+c)-(d+e)的后缀表达式是__________。
A.abcd*++-
B. abc+*de+-
C. abc*+d+-
D. -++*abcd
正确答案: B
10.?? ?假设二叉树结点中都保存有关键字,那么下面的二叉树中:从任一结点出发到根的路径上所经过的结点序列都是按其关键字有序的是__________。
A. 完全二叉树
B. 二叉排序树
C. 满二叉树
D. 大顶堆
正确答案: D
11.?? ?无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},则下面的顶点序列中,__________是该图深度优先遍历的一个正确的输出序列。
A. a,b,e,c,d,f
B. a,c,f,e,b,d
C. a,e,d,f,c,b
D. a,e,b,c,f,d
正确答案: C
======================================
填空题 (总分:4.00)
1.?? ?若一棵深度为6的完全二叉树的第6层有3个叶结点(根结点在第1层),则该二叉树共有叶结点的个数为__________。
正确答案: 17
2.?? ?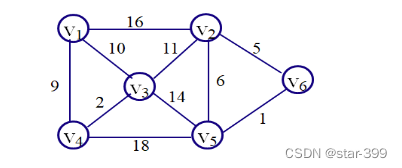
对于上图所示的无向连通图,若采用普里姆(Prim)算法求其最小生成树,假设第一个选择加入最小生成树的顶点为V1,则最后一条加入最小生成树的边的权值为 __________ 。
正确答案: 1
3.?? ?具有20个顶点的无向图采用邻接矩阵表示(两顶点间有边用1表示,无边用0表示),若该图为连通图,则其邻接矩阵中至少有__________个非零元素。
正确答案: 38
4.?? ?给定一组权值:{2,3,4,4,7,8},以这些权值作为叶结点构造哈夫曼树,其带权路径长度为__________。
正确答案: 69
======================================
?编程题(总分:35.00)
| 1. | 机试异常检测(简)A (分值:15.00) |
?
【问题描述】
某教学平台具有考试登录异常检测功能,检测规则如下:
1、考试开始后,如果同一账号在不同机器上登录,系统将报警输出异常登录信息(可能存在私自换机器的情况);
2、考试开始后,如果同一账号在同一机器上多次登录,属于正常情况,系统不报警。
编写程序,读入某次考试学生的登录日志信息,对其进行异常检测,输出异常登录信息。日志信息包括学生学号(即学生账号,唯一标识学生身份的信息,用一整数表示,不超过int的表示范围)、学生姓名(用不含空白符的字符串表示,字符个数不超过15)、机器号(用一整数表示,不超过int的表示范围)、登录时间(用包含6个数字的字符串表示,例如:093756,表示9点37分56秒)。
【输入形式】
先从控制台输入日志信息条数(不超过200条),然后按照登录先后顺序分行输入日志信息,每条信息包括学号、姓名、机器号和登录时间,以一个空格分隔各数据。
【输出形式】
按照学号从小到大的顺序输出登录异常账号信息(仅包括学号和姓名),每条信息独占一行,学号和姓名以一个空格分隔。如果没有异常登录信息,则什么都不输出。
【样例输入】
21
191028 wangdi 15 093000
192387 litong 39 093000
190877 liugang 37 093001
197583 huangqinian 196 093004
195211 liuhao 201 093005
193098 zhaogang 377 093006
190001 zhousheng 1 093007
190009 wuhong 12 093007
197583 huangqinian 197 093008
195877 lisisi 202 093008
192387 litong 309 093009
191000 tonghao 201 093402
197583 huangqinian 196 093500
191028 wangdi 15 093507
190010 wangzhuang 85 093558
195333 zhangye 63 093600
197583 huangqinian 195 094100
195211 liuhao 200 095103
190010 wangzhuang 287 095509
193098 zhaogang 377 095606
191028 wangdi 15 095709
【样例输出】
190010 wangzhuang
192387 litong
195211 liuhao
197583 huangqinian
【样例说明】
输入了21条登录日志信息,其中有四位学生(学号分别为190010、192387、195211和197583)在多台机器上登录,属于异常登录,输出异常账号登录信息;注意:学号为191028的学生在15号机器上有多次登录,属于正常重复登录。
【评分标准】
该题要求辨别输出异常登录信息,提交程序名为login.c。
解答1:
#include <stdio.h>
#include <string.h>
struct log
{
int no, mach;
char name[16], time[7];
};
int main()
{
int n, i, j, k, m, p;
struct log sts[200], es[200], temp;
scanf("%d", &n);
for (i = 0, m = 0, k = 0; i < n; i++)
{
scanf("%d%s%d%s", &temp.no, temp.name, &temp.mach, temp.time);
for (j = 0; j < m; j++)
if (temp.no == sts[j].no)
break;
if (j == m)
sts[m++] = temp;
else if (temp.mach != sts[j].mach)
{
for (p = 0; p < k; p++)
if (temp.no == es[p].no)
break;
if (p == k)
es[k++] = temp;
}
}
for (i = k - 1; i > 0; i--)
for (j = 0; j < i; j++)
if (es[j].no > es[j + 1].no)
{
temp = es[j];
es[j] = es[j + 1];
es[j + 1] = temp;
}
for (i = 0; i < k; i++)
printf("%d %s\n", es[i].no, es[i].name);
return 0;
}?解答2:
#include <stdio.h>
struct node
{
int id;
char name[20];
int machine;
char time[10];
};
int main()
{
int n;
scanf("%d", &n);
struct node list[205] = {};
for (int i = 0; i < n; i++)
scanf("%d%s%d%s", &list[i].id, list[i].name, &list[i].machine, list[i].time);
for (int i = 0; i < n - 1; i++)
{
int ys = 0;
for (int j = 0; j < n - i - 1; j++)
{
if (list[j].id > list[j + 1].id)
{
struct node tmp = list[j];
list[j] = list[j + 1];
list[j + 1] = tmp;
ys = 1;
}
}
if (ys == 0)
break;
}
struct node ans[205] = {};
int ansi = 0;
for (int i = 0; i < n - 1;)
{
int ys = 0;
int j = i + 1;
for (j = i + 1; list[i].id == list[j].id; j++)
{
if (list[i].machine != list[j].machine)
ys = 1;
}
if (ys == 1)
{
ans[ansi++] = list[i];
}
i = j;
}
for (int i = 0; i < ansi; i++)
printf("%d %s\n", ans[i].id, ans[i].name);
return 0;
}| 2. | 函数调用关系A (分值:10.00) |
?
【问题描述】
给定某能正常运行结束的用户函数调用栈信息(当一个函数被调用时将入栈,当调用返回时,将出栈)。编写程序,对函数调用栈信息进行分析,依据函数入栈和出栈信息,分析函数调用关系,即一个函数调用了哪些不同函数。并按运行时调用序输出调用关系。
说明:
1. 在一个函数中,同一函数有可能被调用多次,输出调用关系时只输出一次;若一个函数没有调用其它函数,则不输出调用关系;
2. 函数运行时调用序是指函数在调用栈中的出现序。
3. 程序中不存在递归调用。函数名符合C语言标识符的规定,函数名长度不超过20,每个函数最多调用不超过10个不同函数,程序中用户定义的函数个数不超过100。
算法提示:当一个函数入栈时,它就是当前栈顶函数调用的一个函数。
【输入形式】
假设用8表示函数入栈操作;用0表示当前函数出栈。当操作为8(入栈)时,输入形式为:
<操作> <函数名>??
当操作为0(出栈)时,输入形式为:
<操作>
所有入栈操作和出栈操作都是从标准输入分行输入,假设调用栈中函数个数最多不超过200。开始时,调用栈为空,当调用栈再次为空时,输入结束。
【输出形式】
按运行时调用先后顺序输出函数调用关系到标准输出,每行为一个函数的调用关系信息,包括:函数名及被调用函数,函数与被调用函数间用一个英文冒号“:”分隔,被调用函数间用一个英文逗号“,”分隔,最后一个函数名后跟一个回车。若一个函数没有调用其它函数,则不输出。
【样例输入】
8 main
8 input
0
8 mysqrt
0
8 findA
0
8 findB
8 area
8 mysin
0
8 mycos
0
8 mysqrt
0
0
0
8 findC
8 area
8 mysin
0
0
8 mysqrt
8 max
0
0
0
8 output
0
0
【样例输出】
main:input,mysqrt,findA,findB,findC,ouput
mysqrt:max
findB:area
area:mysin,mycos,mysqrt
findC:area,mysqrt
【样例说明】
按照运行时调用函数的先后顺序,依次输出了main、mysqrt、findB、area和findC的函数调用关系。其中main函数调用了6个函数,按照运行时调用序依次输出。注意:mysqrt函数先于findB等函数出现在栈中,虽然mysqrt调用max较晚,但要先输出其调用关系。
【评分标准】
该题要求对函数调用栈信息进行分析,提交程序名为stack.c
解答1:
#include <stdio.h>
#include <string.h>
struct func
{
char name[21];
char cf[10][21];
int n;
};
int main()
{
int i, j, k, m, top;
char st[200][21], fun[21];
struct func fs[100];
m = 0;
top = -1;
do
{
scanf("%d", &k);
if (k == 8)
{
scanf("%s", fun);
for (i = 0; i < m; i++)
if (strcmp(fs[i].name, fun) == 0)
break;
if (i == m)
{
strcpy(fs[m].name, fun);
fs[m++].n = 0;
}
if (top >= 0)
{
for (i = 0; i < m; i++)
if (strcmp(fs[i].name, st[top]) == 0)
break;
for (j = 0; j < fs[i].n; j++)
if (strcmp(fs[i].cf[j], fun) == 0)
break;
if (j == fs[i].n)
{
strcpy(fs[i].cf[j], fun);
fs[i].n++;
}
}
strcpy(st[++top], fun);
}
else
top--;
} while (top > -1);
for (i = 0; i < m; i++)
if (fs[i].n > 0)
{
printf("%s:", fs[i].name);
for (j = 0; j < fs[i].n - 1; j++)
printf("%s,", fs[i].cf[j]);
printf("%s\n", fs[i].cf[j]);
}
return 0;
}?解答2:
#include <stdio.h>
#include <string.h>
int main()
{
int operation;
char func[105][25] = {};
int funci = 1;
int stack[205] = {}, stacki = 0;
int ans[105][15] = {};
while (scanf("%d", &operation) != EOF)
{
if (operation == 0)
{
--stacki;
}
else if (operation == 8)
{
char f[25] = {};
scanf("%s", f);
int index = 0;
for (int i = 1; i < funci; i++)
{
if (strcmp(func[i], f) == 0)
{
index = i;
break;
}
}
if (index == 0)
{
index = funci;
for (int j = 0; f[j] != '\0'; j++)
func[index][j] = f[j];
funci++;
}
int top = stack[stacki - 1], ys = 0, a = 0;
for (int i = 0; i < 15; i++)
{
if (ans[top][i] == index)
{
ys = 1;
break;
}
if (ans[top][i] == 0)
{
ys = 2;
a = i;
break;
}
}
if (ys == 2)
{
ans[top][a] = index;
}
stack[stacki++] = index;
}
}
for (int i = 1; i < funci; i++)
{
if (ans[i][0] != 0)
{
printf("%s:", func[i]);
for (int j = 0; ans[i][j] != 0; j++)
{
int tmp = ans[i][j];
printf("%s", func[tmp]);
if (ans[i][j + 1] != 0)
printf(",");
else
printf("\n");
}
}
}
return 0;
}| 3. | 服务优化A (分值:10.00) |
?
【问题描述】
假设某机场所有登机口(Gate)呈树形排列(树的度为3),安检处为树的根,如下图所示。图中的分叉结点(编号大于等于100)表示分叉路口,登机口用小于100的编号表示(其一定是一个叶结点)。通过对机场所有出发航班的日志分析,得知每个登机口每天的平均发送旅客流量。作为提升机场服务水平的一个措施,在不改变所有航班相对关系的情况下(即:出发时间不变,原在同一登机口的航班不变),仅改变登机口(例如:将3号登机口改到5号登机口的位置),使得整体旅客到登机口的时间有所减少(即:从安检口到登机口所经过的分叉路口最少)。

?
?
编写程序模拟上述登机口的调整,登机口调整规则如下:
1)首先按照由大到小的顺序对输入的登机口流量进行排序,流量相同的按照登机口编号由小到大排序;
2)从上述登机口树的树根开始,将登机口按照从上到下(安检口在最上方)、从左到右的顺序,依次对应上面排序后将要调整的登机口。
例如上图的树中,若只考虑登机口,则从上到下有三层,第一层从左到右的顺序为:5、6、14、13,第二层从左到右的顺序为:7、8、9、10、1、2、18、17、16、15,第三层从左到右的顺序为:11、12、3、4、20、19。若按规则1排序后流量由大至小的前五个登机口为3、12、16、20、15,则将流量最大的3号登机口调整到最上层且最左边的位置(即:5号登机口的位置),12号调整到6号,16号调整到14号,20号调整到13号,15号调整到第二层最左边的位置(即7号登机口的位置)。
【输入形式】
1)首先按层次从根开始依次输入树结点之间的关系。其中分叉结点编号从数字100开始(树根结点编号为100,其它分叉结点编号没有规律但不会重复),登机口为编号小于100的数字(编号没有规律但不会重复,其一定是一个叶结点)。树中结点间关系用下面方式描述:
R S1 S2 S3 -1
其中R为分叉结点,从左至右S1,S2,S3分别为树叉R的子结点,其可为树叉或登机口,由于树的度为3,S1,S2,S3中至多可以2个为空,最后该行以-1和换行符结束。各项间以一个空格分隔。如:
100 101 102 103 -1
表明编号100的树根有三个子叉,编号分别为101、102和103,又如:
104 7 8 -1?
表明树叉104上有2个编号分别为7和8的登机口。
假设分叉结点数不超过100个。分叉结点输入的顺序不确定,但可以确定:输入某个分叉结点信息时,其父结点的信息已经输入。
输入完所有树结点关系后,在新的一行上输入-1表示树结点关系输入完毕。
2)接下来输入登机口的流量信息,每个登机口流量信息分占一行,分别包括登机口编号(1~99之间的整数)和流量(大于0的整数),两整数间以一个空格分隔。登机口数目与前面构造树时的登机机口数目一致。
【输出形式】
按照上述调整规则中排序后的顺序(即按旅客流量由大到小,流量相同的按照登机口编号由小到大)依次分行输出每个登机口的调整结果:先输出调整前的登机口编号,然后输出字符串"->"(由英文减号字符与英文大于字符组成),再输出要调整到的登机口编号。
【样例输入】
100 101 102 103 -1
103 14 108 13 -1
101 5 104 6 -1
104 7 8 -1
102 105 106 107 -1
106 1 110 2 -1
108 16 15 -1
107 18 111 17 -1
110 3 4 -1
105 9 109 10 -1
111 20 19 -1
109 11 12 -1
-1
17 865
5 668
20 3000
13 1020
11 980
8 2202
15 1897
6 1001
14 922
7 2178
19 2189
1 1267
12 3281
2 980
18 1020
10 980
3 1876
9 1197
16 980
4 576
【样例输出】
12->5
20->6
8->14
19->13
7->7
15->8
3->9
1->10
9->1
13->2
18->18
6->17
2->16
10->15
11->11
16->12
14->3
17->4
5->20
4->19
【样例说明】
样例输入了12条树结点关系,形成了如上图的树。然后输入了20个登机口的流量,将这20个登机口按照上述调整规则1排序后形成的顺序为:12、20、8、19、7、15、3、1、9、13、18、6、2、10、11、16、14、17、5、4。最后按该顺序将所有登机口按照上述调整规则2进行调整,输出调整结果。
【评分标准】
该题要求计算并输出登机口的调整方法,提交程序名为adjust.c。
解答1:
#include <stdio.h>
#include <stdlib.h>
struct node
{
int no;
struct node *l, *m, *r;
};
struct gate
{
int no, t;
};
struct node *find(struct node *root, int n1)
{
struct node *p;
if (root->no == n1)
return root;
if (root->l != NULL)
{
p = find(root->l, n1);
if (p != NULL)
return p;
}
if (root->m != NULL)
{
p = find(root->m, n1);
if (p != NULL)
return p;
}
if (root->r != NULL)
{
p = find(root->r, n1);
if (p != NULL)
return p;
}
return NULL;
}
int main()
{
int i, j, m, n, f, r, n1, n2, n3, n4, max;
struct node *root, *que[201], *p;
struct gate gs[100], temp;
root = NULL;
n = 0;
while (1)
{
scanf("%d", &n1);
if (n1 == -1)
break;
if (root == NULL)
{
root = (struct node *)malloc(sizeof(struct node));
root->no = n1;
p = root;
}
else
p = find(root, n1);
scanf("%d", &n2);
if (n2 != -1)
{
p->l = (struct node *)malloc(sizeof(struct node));
p->l->no = n2;
p->l->l = p->l->m = p->l->r = NULL;
if (n2 < 100)
n++;
}
else
{
p->l = p->m = p->r = NULL;
continue;
}
scanf("%d", &n3);
if (n3 != -1)
{
p->m = (struct node *)malloc(sizeof(struct node));
p->m->no = n3;
p->m->l = p->m->m = p->m->r = NULL;
if (n3 < 100)
n++;
}
else
{
p->m = p->r = NULL;
continue;
}
scanf("%d", &n4);
if (n4 != -1)
{
p->r = (struct node *)malloc(sizeof(struct node));
p->r->no = n4;
p->r->l = p->r->m = p->r->r = NULL;
if (n4 < 100)
n++;
scanf("%d", &m);
}
else
p->r = NULL;
}
for (i = 0; i < n; i++)
scanf("%d%d", &gs[i].no, &gs[i].t);
for (i = 0; i < n; i++)
{
max = i;
for (j = i + 1; j < n; j++)
if ((gs[max].t < gs[j].t) || (gs[max].t == gs[j].t && gs[max].no > gs[j].no))
max = j;
if (max != i)
{
temp = gs[i];
gs[i] = gs[max];
gs[max] = temp;
}
}
i = 0;
que[0] = root;
f = 0;
r = 0;
while (f <= r)
{
p = que[f++];
if (p->no < 100)
printf("%d->%d\n", gs[i++].no, p->no);
if (p->l != NULL)
que[++r] = p->l;
if (p->m != NULL)
que[++r] = p->m;
if (p->r != NULL)
que[++r] = p->r;
}
return 0;
}解答2:
#include <stdio.h>
struct node
{
int id;
int num;
struct node *father;
struct node *child[3];
};
int main()
{
struct node list[205] = {};
for (int i = 0; i < 205; i++)
{
list[i].id = i;
list[i].num = 0;
list[i].father = list[i].child[0] = list[i].child[1] = list[i].child[2] = NULL;
}
struct node *root = &list[100];
int r = 0, count = 0;
while (1)
{
scanf("%d", &r);
if (r == -1)
break;
int s = 0, i = 0;
while (1)
{
scanf("%d", &s);
if (s == -1)
break;
list[r].child[i] = &list[s];
list[s].father = &list[r];
if (s < 100)
count++;
i++;
}
}
for (int i = 0; i < count; i++)
{
int s = 0;
scanf("%d", &s);
scanf("%d", &(list[s].num));
}
struct node sort[105] = {};
for (int i = 0; i < 100; i++)
sort[i] = list[i];
for (int i = 0; i < 99; i++)
{
int ys = 0;
for (int j = 0; j < 99 - i; j++)
{
if (sort[j].num < sort[j + 1].num)
{
struct node tmp = sort[j];
sort[j] = sort[j + 1];
sort[j + 1] = tmp;
ys = 1;
}
}
if (ys == 0)
break;
}
int ans[105] = {}, ansi = 0;
struct node *queue[105] = {};
int a = 0, b = -1;
struct node *t = root, *p = NULL;
if (t != NULL)
{
queue[0] = t;
while (b < a)
{
p = queue[++b];
if (p->id < 100)
ans[ansi++] = p->id;
for (int i = 0; i < 3; i++)
{
if (p->child[i] != NULL)
queue[++a] = p->child[i];
}
}
}
for (int i = 0; i < count; i++)
{
printf("%d->%d\n", sort[i].id, ans[i]);
}
return 0;
}