六、排序
大纲
六、排序
(一)排序的基本概念 (二)插入排序
1.直接插入排序
2.折半插入排序 (三)气泡排序(bubble sort) (四)简单选择排序 (五)希尔排序(shell sort)
(六)快速排序 (七)堆排序
(八)二路归并排序(merge sort) (九)基数排序
(十)外部排序 (十一)排序算法的分析与应用
分类及稳定性分析
根据是否在内存中进行分类·分为 : 内排序与外排序
内排序分为需要关键字比较的排序(插排、选择、交换、归并)和 不需要的(基数排序)
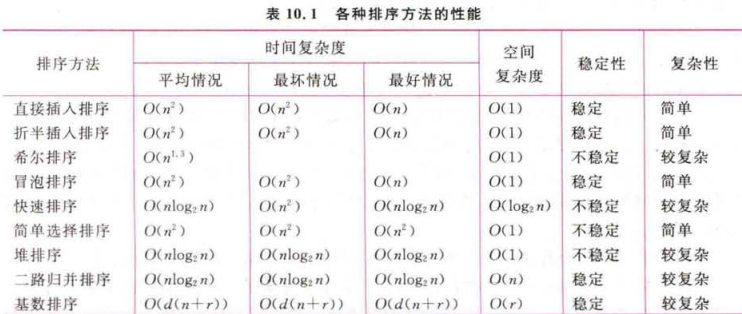
总体上分为(这里就按升序写了) :
| 1.插入排序 : 从无序区选择一个插入前面有序区,空间均为O(1), 时间O(n^2)、正序时最好 n, 每次插入后有序区不是全局有序,之后还会调整位置 | 稳定性 | 性能比较 | 时间 | |||
|---|---|---|---|---|---|---|
| 直接插入排序 : 每次将无序区第一个元素与前面依次比较大小交换,本就正序时间O(n) | 稳定 | 总比较次数最多,移动次数一样 | ||||
| 折半插入排序 : 在有序区二分查找位置,再集中向后移动插入 | 稳定 | 比较次数少,优于直接 | ||||
| 希尔排序 : 将其等间隔分组,对每组进行直接插排,依次调小间隔,直至间隔为1 | 不稳定 | 平均时间认为n^1.3,性能比直接优越 | ||||
| 2. 选择排序 : 每次选择一个无序区的最值与交换到无序区的边界,加入有序区,每次选择交换后,有序区是全局有序的,空间O(1) | ||||||
| 简单选择排序 : 每次选择一个最小的元素放到前面 | 稳定 | O(n^2) | ||||
| 堆排序 : 先要建立大根堆,之后每次将堆顶与后面交换,再将现在的堆顶下沉,循环 | 不稳定 | 建堆时间O(n),调整时间O(h),h为树高 | O(n*logn) | |||
| 3. 交换排序 有序区是全局有序的,空间O(1) | ||||||
| 冒泡排序 : 从后面相邻两个依次比较交换,将最小冒到前面 | 稳定 | O(n^2) | ||||
| 快速排序 : 以某个值为中心,让其左边都是小的,右边都是大的,左右递归 | 不稳定 | 平均(nlogn),最好nlogn,最坏n^2,正序/反序时最坏 | ||||
| 4.归并排序 二路归并,需要开一个辅助数组,空间O(n) | 稳定 | nlogn | ||||
| 5.基数排序 : 分别从低到高以各位的数字进行排序,空间O? | 稳定 | O(d(r+n)) |
代码
【模板】快速排序
题目描述
利用快速排序算法将读入的 N N N 个数从小到大排序后输出。
快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料,掌握后独立完成。(C++ 选手请不要试图使用 STL,虽然你可以使用 sort 一遍过,但是你并没有掌握快速排序算法的精髓。)
输入格式
第 1 1 1 行为一个正整数 N N N,第 2 2 2 行包含 N N N 个空格隔开的正整数 a i a_i ai?,为你需要进行排序的数,数据保证了 A i A_i Ai? 不超过 1 0 9 10^9 109。
输出格式
将给定的 N N N 个数从小到大输出,数之间空格隔开,行末换行且无空格。
样例 #1
样例输入 #1
5
4 2 4 5 1
样例输出 #1
1 2 4 4 5
提示
对于 20 % 20\% 20% 的数据,有 N ≤ 1 0 3 N\leq 10^3 N≤103;
对于 100 % 100\% 100% 的数据,有 N ≤ 1 0 5 N\leq 10^5 N≤105。
这道题用快排需要对基准选择优化才能满分,这里就用了一个最简单的优化算了,80分,毕竟just练习各大排序的模板
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int arr[N];
int tt[N];//归并排序的辅助数组
int n;
void quickSort(int nums[], int l, int r){
if(l > r) return;
int ll = l, rr = r;
if(r - l >= 10){
int x = rand() % (r - l + 1) + l;
// int mid = ll + rr >> 1;
int mid = x;
swap(nums[ll], nums[mid]);
}
int t = nums[ll];
while(ll < rr){
while(ll < rr && nums[rr] >= t) rr --;
while(ll < rr && nums[ll] <= t) ll ++;
if(ll < rr) swap(nums[ll], nums[rr]);
}
swap(nums[l], nums[ll]);
quickSort(nums, l, ll - 1);
quickSort(nums, ll + 1, r);
}
void mergeSort(int nn[], int l, int r){
if(l >= r) return;
int mid = l + r >> 1;
mergeSort(nn, l, mid);
mergeSort(nn, mid + 1, r);
int l1 = l, l2 = mid + 1, ind = l;
while(l1 <= mid && l2 <= r){
if(n[l1] <= nn[l2])
tt[ind ++] = nn[l1 ++];
else
tt[ind ++] = nn[l2 ++];
}
while(l1 <= mid) tt[ind ++] = nn[l1 ++];
while(l2 <= r) tt[ind ++] = nn[l2 ++];
for(int i = l; i <= r; i ++)
nn[i] = tt[i];
}
void sift(int a[], int l, int r){
int i = l, j = 2 * i + 1;
while(j <= r){
int big;
if(j + 1 <= r) big = a[j] >= a[j + 1] ? j : j + 1;
else big = j;
if(a[i] < a[big]){
swap(a[i], a[big]);
i = big, j = 2 * i + 1;
}else return;
}
}
void heapSort(int a[], int l, int r){
//初始化建堆
for(int i = r / 2; i >= 0; i --)
sift(a, i, r);
for(int i = r; i >= 1; ){
swap(a[0], a[i --]);
sift(a, 0, i);
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
scanf("%d", arr + i);
heapSort(arr, 0, n - 1);
for(int i = 0; i < n; i ++)
printf("%d ", arr[i]);
puts("");
return 0;
}
