应对笔试手写代码,如何准备动态规划?
1. 动态规划题目的特点
遇到一个题目,首先要区分是用动态规划来解答,还是用递归来解答。
动规题目特点:完成一个任务,有多个步骤,每个步骤可以有不同的选择,动态规划是让你求完成任务时总共有多少种选择,而递归要求你把每次的选择过程都记录下来。

动态规划的特点主要有以下三种,在这里我举一个更加具体的例子给大家理解。
假如我的家乡是在城市A,我上学的地方是城市B,那么如果题目问题“请问你从家乡到上学的地方的路线有哪些,请列举出来,这种就是用递归”,而如果问“请问你从家乡到上学的地方有多少种路线?”或“请问你从家乡到上学的地方最短的路线是哪一条?”或“请问是否有一条路线能从家乡到学校?”这就是对应着上面三种题型。
那他们有什么共同点呢?我随手给大家画了这个图
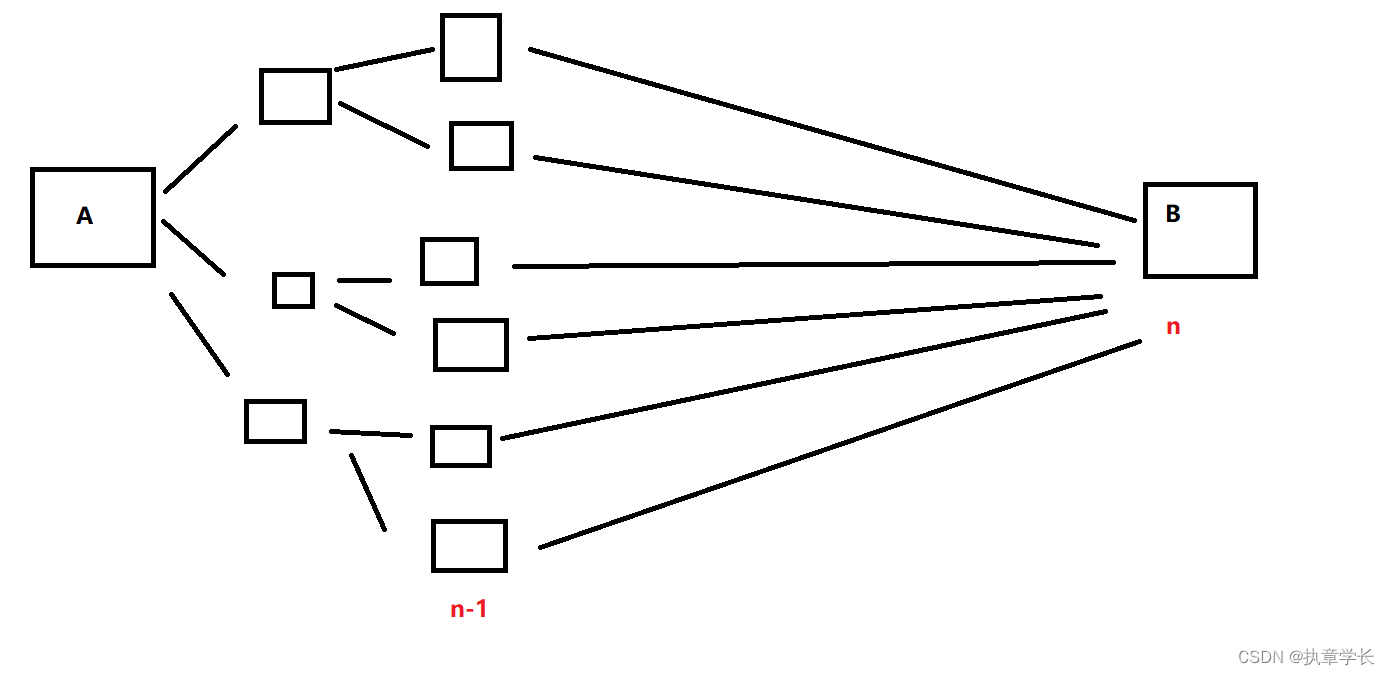
我们发现对于第一个问题,我们想知道从A到B有几种路线,那不就等于求从 A 到 n-1 层的路线共有多少种吗?而第二个问题就会转为求(到达 n-1 层的距离+从n-1层到B的距离)最短的路线,而最后一个问题就会转为在 n-1 层中选出可以从 A 到达的并且可以从 n-1 层到达B的。
那么他们的共同点就是,我们想要求第n层的数据,可以通过求第n-1层的各个数据,然后根据条件筛选出一个最合适的,而求第n-1层又可以通过n-2层来求得…以此类推,我们只需要求出最开始的初始状态即可,而通常初始状态都是已知的(例如这道题,到达第一层的数据,很容易得出吧)。那么我们写代码时只需要通过将思考方向转过来,开辟一个n的空间(通常是数组),从初始状态开始存,结合for循环计算到最后一个的数据即可。
2. 确认为动态规划题目后分析步骤
动态规划题目拿到时需要分析的:
1、确定状态
先尝试分析最后一步可以由前面哪些步骤得来(注意这里不一定是找n-1步,要具体情况具体分析)。
2、转移方程
根据1中的关系推演出整个过程的一般化公式。
第一种,求种数。f(x) = f(x-1)+f(x-2)…
第二种,求最大值最小值。f(x) = max(x-1,x-2)…
第三种,求是否。f(x) = f(x-1) && 结合其他条件…
注意以上三种对应的公式只是表示一个例子,具体到题目中要具体分析。
3、初始条件和边界条件
初始条件:f(0) = 一般题目会给或者很容易得到。
边界条件:具体题目具体分析是否有需要排除的情况。
4、循环计算
f(0)、f(1) 、f(2)…f(n)。
一般由初始条件开始,利用前面计算好的数据推演接下来的数据。
在这里插入图片描述
3. 动态规划题目模板
动态规划大致模板:
1、定义dp数组(可能时一维或二维等)。
2、找到初始值并赋值到dp中。
3、for循环处理dp中的每个值,对应每一个子问题的解,此时需要用到状态转移方程。
4、返回题目需要的答案。(例如可能为dp(n))
多维度的动态规划:
上面我们说到动态规划可以分为三种,而每一种都有可能出现二维的情况,不慌,这个时候的分析步骤和代码模板几乎和一维一致。区别在于,此时可能需要二维数组来存储,并且需要两个for循环。
4. 常见的动态规划类型

5. 动态规划空间复杂度优化
动态规划的空间复杂度优化:
一般可以通过复用空间来实现。举个例子,当我们在写dp数组的时候发现,状态转移方程是 f(x) = f(x-1) +xxx,那我们其实只需要记录两个变量就好了,用这两个变量记录前后两个值,这一次赋值的变量下一次就会变成前一个层次的变量,不断复用,就不需要dp数组了。空间复杂度就从o(n)到o(1)。同样的二维的也可以通过压缩来降低空间复杂度,例如可以通过取余操作,将原本存储在 5 位置的值通过取余2得到1,从而存储在1的位置(当然,前提是1的值不在需要被使用了,才可以这样赋值掉)。
