文章目录
最短路径问题
典型用途
交通网络的问题——从甲地到乙地之间是否有公路连通?在有多条通路的情况下,哪一条路最短?
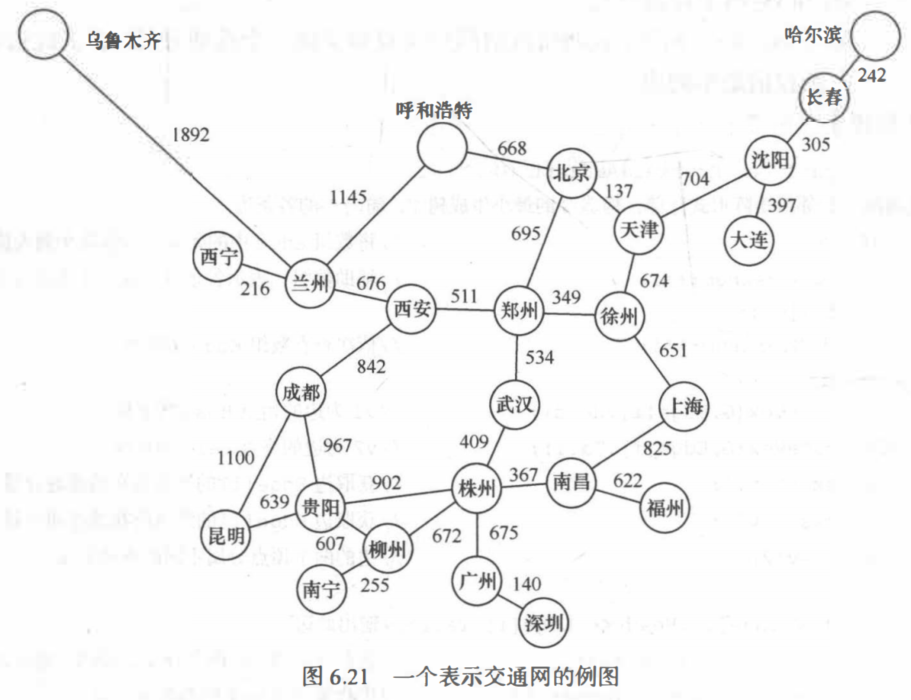
交通网络用有向图来表示:
顶点——表示地点,
弧——表示两个地点有路连通,
弧上的权值——表示两地点之间的距离、交通费或图中所花费的时间等。
如何能够使一个地点到另一个地点的运输时间最短或运费最省?这就是一个求两个地点间的最短路径的问题。
问题抽象
在有向网中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径。
最短路径与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n-1条边。
引出问题
第一类问题:两点间最短路径
用Dijkstra(迪杰斯特拉)算法。
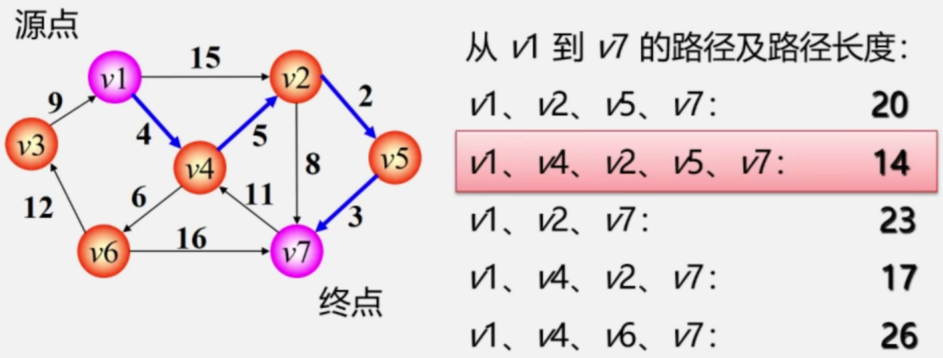
第二类问题:某源点到其他各点最短路径
用Floyd(弗洛伊德)算法。

Dijistra算法
(1)初始化:先找出从源点v0到各终点vk的直达路径(v0, vk),即通过一条弧到达的路径。
(2)选择:从这些路径中找出一条长度最短的路径(v0, u)。
(3)更新:然后对其余各条路径进行适当调整:
若在图中存在弧(u, vk),且(v0, u) + (u, vk) < (v0, vk),则以路径(v0, u, vk)代替(v0, vk)。
在调整后的各条路径中,再找长度最短的路径,以此类推。
void ShortestPath_DIJ(AMGraph G, int v0)
{ // 用Dijkstra算法求有向网G的vO顶点到其余顶点的最短路径
n=G.vexnum; // n为G 中顶点的个数
for(v= O;v<n; ++v) // n个顶点依次初始化
{
S[v]=false; // S初始为空集
D[v]=G.arcs[v0][v]; // 将v0到各个终点的最短路径长度初始化为弧上的权值
if(D[v]<Maxlnt) Path[v]=vO; // 如果v0和v之间有弧, 则将v的前驱置为v0
else Path[v]=-1; // 如果v0 和v之间无弧, 则将v的前驱置为-1
}
S[v0] = true; // 将v0加人 S
D[v0]=0; // 源点到源点的距离为 0
/*--------初始化结束, 开始主循环, 每次求得vO到某个顶点v的最短路径, 将v加到s集----*/
for(i=1;i<n;++i) // 对其余 n-1个顶点,依次进行计算
{
min=MaxInt;
for(w= O;w<n;++w)
if(!S[w]&&D[w]<min)
{v=w;min=D[w];} // 选择一条当前的最短路径,终点为v
S[v]=true; // 将v加入S
for(w=0;w<n;++w) // 更新从v0出发到集合V-S上所有顶点的最短路径长度
if(!S[w]&&(D[v]+G.arcs[v][w]<D[w]))
{
D[w]=D[v]+G.arcs[v][w]; // 更新D[w]
Path[w]=v; // 更改w的前驱为v
}
}
}
迪杰斯特拉(Dijkstra)算法描述
按路径长度递增次序产生最短路径
1.把V分成两组:
(1)S:已求出最短路径的顶点的集合。
(2)T=V-S:尚未确定最短路径的顶点集合。
2.将T中顶点按最短路径递增的次序加入到S中,保证:
(1)从源点v0到S中各顶点的最短路径长度都不大于从v0到T中任何顶点的最短路径长度。
(2)每个顶点对应一个距离值:
S中顶点:从v0到此顶点的最短路径长度。
T中顶点:从v0到此顶点的只包括S中顶点作中间顶点的最短路径长度。
算法步骤
初始时令S={v0},T={其余顶点}。
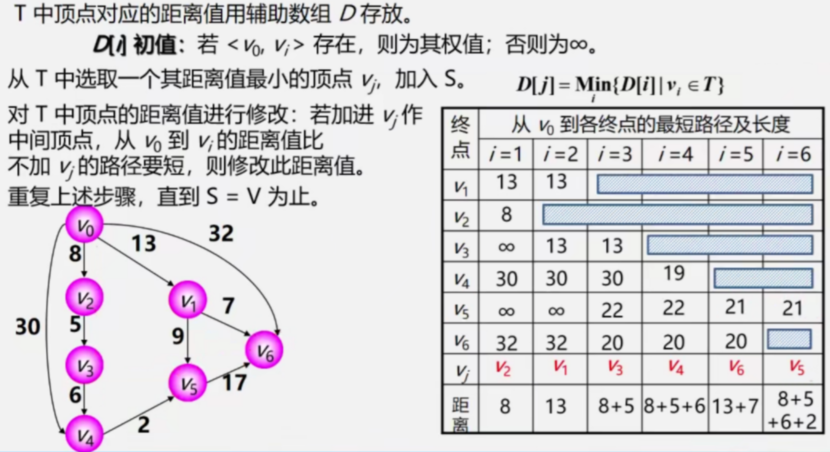
实例
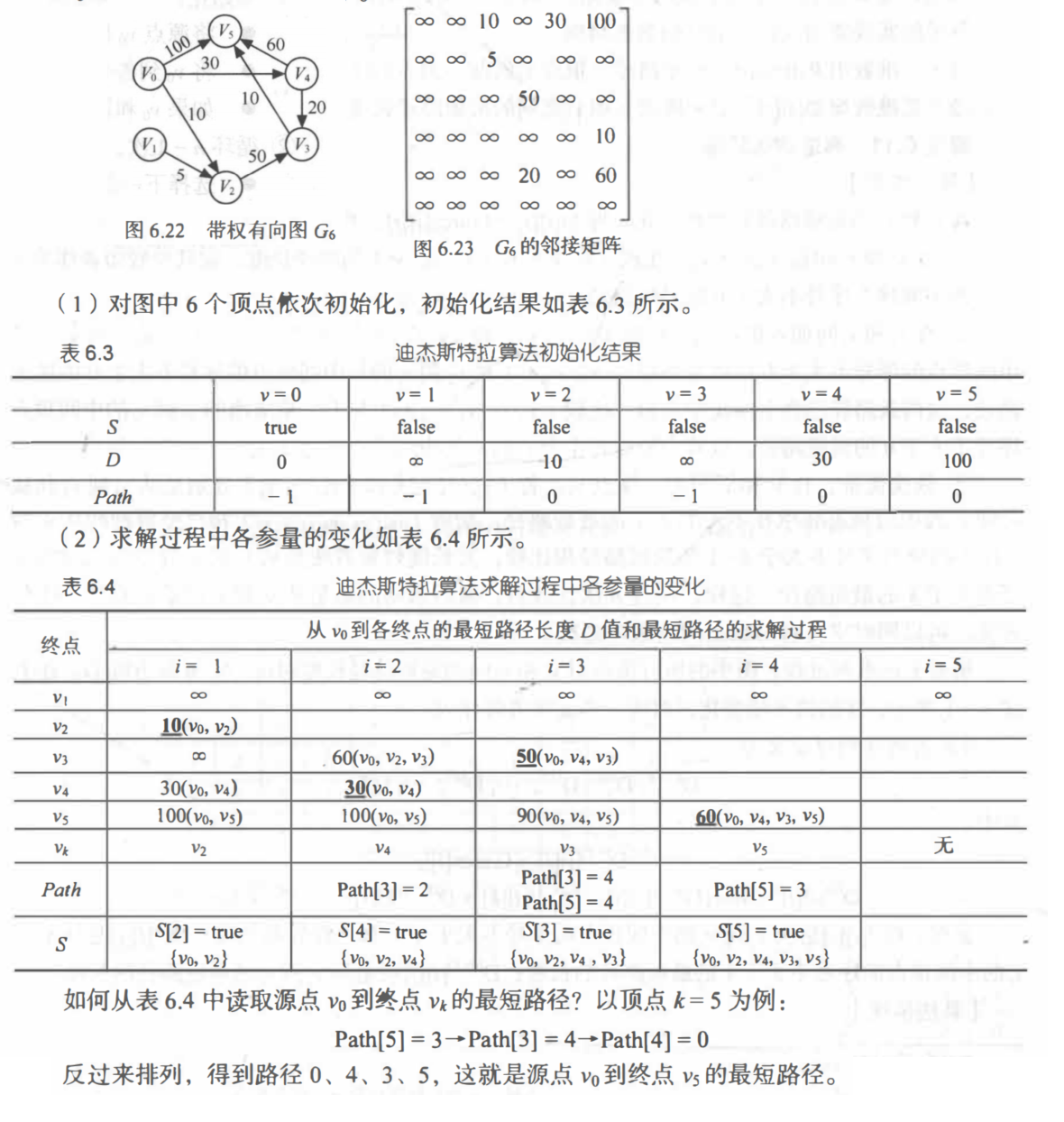
弗洛伊德(Floyd)算法
初始时设置一个n阶方阵,令其对角线元素为0,若存在弧<vi, vj>,则对应元素为权值;否则为∞。
逐步试着在原直接路径中增加中间顶点,若加入中间顶点后路径变短,则修改之;否则,维持原值。所有顶点试探完毕,算法结束。
void ShortestPath_Floyd(AMGraph G)
{ //用Floyd算法求有向网G中各对顶点i和j之间的最短路径
for (i=O; i < G.vexnum; ++i) // 各对结点之间初始已知路径及距离
for(j=O;j <G.vexnum;++j)
{
D[i][j] =G.arcs [i][j];
if(D[i][j]<Maxint) Path[i][j]=i; //如果 i和j 之间有弧,则将j的前驱置为i.
else Path[i][j]=-1; // 如果 i和j 之间无弧,则将j的前驱置为-1
}
for (k=O; k < G.vexnum; ++k)
for (i=O; i <G.vexnum;++i)
for(j=O;j <G.vexnum;++j)
if(D[i][k]+D[k][j] <D[i][j]) // 从i经k到j的一条路径更短
{
D[i][j]=D[i][k]+D[k][j]; // 更新D[i][j]
Path[i][j]=Path[k][j]; // 更改j的前驱为k
}
}
算法思想
- 逐个顶点试探;
- 从vi到vj的所有可能存在的路径中;
- 选出一条长度最短的路径。
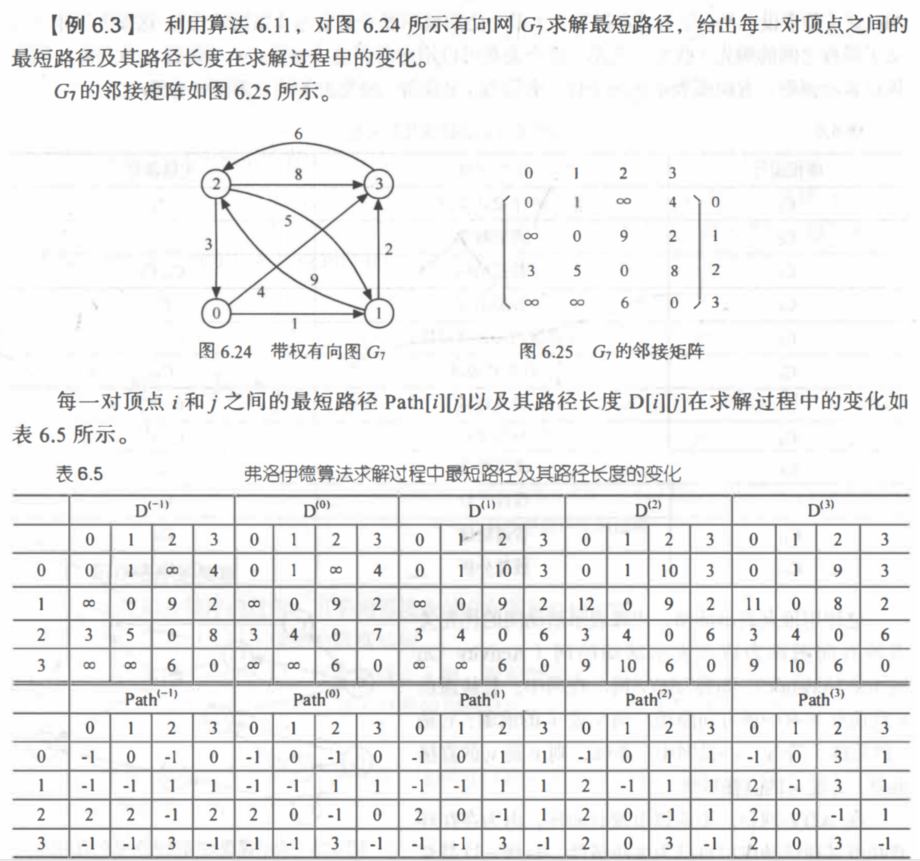
实例