【100个python算法超详细讲解@谷哥技术】
1.问题描述
本节要研究孪生素数的问题,先来看看什么是孪生素数。
所谓孪生素数指的是间隔为2的两个相邻素数,因为它们之间的距离已经
近得不能再近了,如同孪生兄弟一样,故将这一对素数称为孪生素数。
显然,最小的一对孪生素数是(1,3)。我们可以写出3~100以内的孪生素
数,一共有8对,分别是(3,5),(5,7),(11,13),(17,19),(29,31),(41,43),
(59,61)和(71,73)。随着数字的增大,孪生素数的分布也越来越稀疏,人工寻找
孪生素数变得非常困难。
关于孪生素数还存在着一个著名的猜想——孪生素数猜想,即孪生素数是
否有无穷多对,这是数论中还有待解决的一个重要问题。此处我们只讨论在有
限范围内的孪生素数求解问题。
本节要解决的问题:编程求出3~1000以内的所有孪生素数。
2.问题分析
只要明白了什么是孪生素数,该问题便很好理解了。下面我们给出孪生素
数更准确的定义。
孪生素数是指若a为素数,且a+2也是素数,则素数a和a+2称为孪生素数。
要编程求解的问题是找出3~1000以内的所有孪生素数,因此很自然的可
以使用穷举法对3~1000以内的每一个整数n进行考查,先判断n是否为素数,
再判断n+2是否为素数,如果n和n+2同时为素数,则(n,n+2)就是一对孪生素
数,将其打印输出即可。
读者根据输出结果便可获知3~1000以内的孪生素数共有多少对。
3.算法设计
在问题分析中我们已经确定要采用穷举法逐一考查3~1000以内的每个整
数,因此在本题的算法设计中需要采用循环结构。
在判断是否为素数时可以定义一个函数prime,每次判断整数n是否为素数
时都将n作为实参传递给函数prime(),在prime()中使用前面介绍过的判断素数
的方法进行判断。如果n为素数,则prime()函数返回值为1,否则prime()函数返
回值为0。
4.确定程序框架
程序的流程图如图5.11所示。
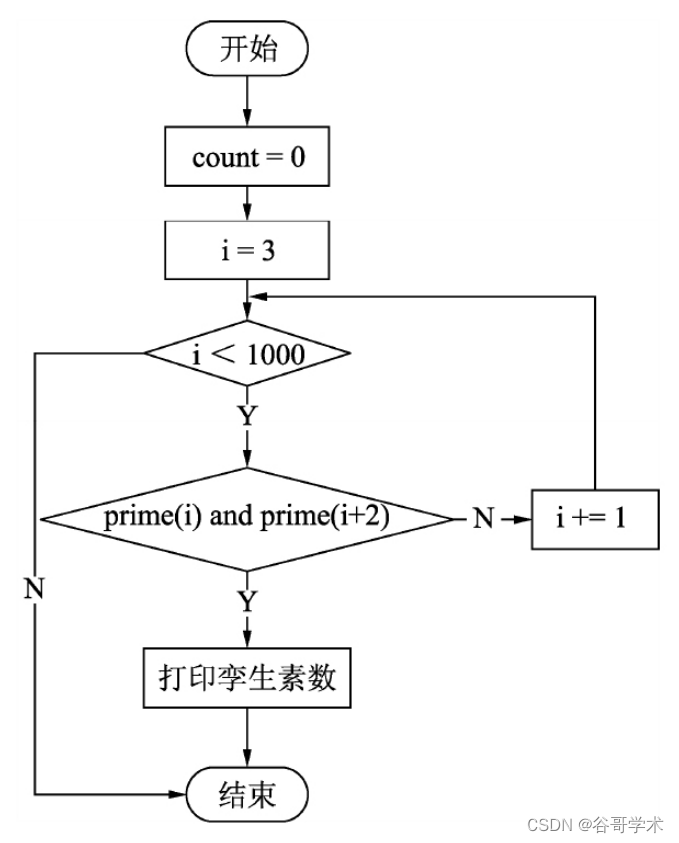
5.完整的程序
根据上面的分析,编写程序如下:?
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 孪生素数
import math
# 判断n是否为素数
def prime(n):
k = math.sqrt(n) + 1
i = 2
while i <= k:
if n % i == 0:
return 0 # n能被j整除,不是素数,返回0
i += 1
return 1 # n是素数,返回1
if __name__=="__main__":
count = 0 # 计数器
print("3到1000之间的孪生素数:")
for i in range(3, 1000):
if prime(i) and prime(i+2):
print("(%-3d, %3d) " %(i, i+2), end="")
count += 1
if count % 5 == 0: # 每5个数换一行
print()
print("\n1000以内的孪生素数共有%d对" %count)6.运行结果
在PyCharm下运行程序,结果如图5.12所示。

观察图5.12可知,输出结果时每行都打印了5对孪生素数,一共打印了7
行。因此,在3~1000范围内的孪生素数一共有35对。?