《基于eigen3多层感知机的反向传播算法实现》

Deep learning 现在有四大范式 MLP、CNN、RNN、Attention，一般feature extractor会是CNN、RNN，semantic info都会MLP、attention所获得

为了自适应地拥有最好的权重，他们都不开反向传法算法，或者是bp-based的训练方法（e.g. rnn有BPTT）

所以，做为cpp课设，很有价值基于链表手写复现其中最为简单的MLP

1.目标：只用线性代数库实现反向传播算法并验证通用近似定理（不可解释的级别、可解释可视化是后续工作）

这里我们验证的是多层感知机，即$ \phi(.) $本质是复合函数的情况
loss为平方误差损失函数 $MSE(y, y_{predict}) = (y - y_{predict})^2$
选择的激活函数仅为relu，即 $\begin{cases}x , x>0 \\ 0, x \le 0\end{cases}$
误差衡量标准为相对误差，即$ Error = \frac{|\delta|}{S_{true}} $

2. CmakeList 与 Eigen3

本次项目，仅调用Eigen作为线性代数库（无MKL后端）完成矩阵乘法等代数运算Eigen: The Matrix class

先上我的cmakelist, 非常esay

cmake_minimum_required(VERSION 3.20)
project(MLP_BP)

set(CMAKE_CXX_STANDARD 11)
include_directories(D:\\eigen\\eigen-3.4.0\\eigen-3.4.0)
include_directories(D:\\Originalcodes\\Field_of_C++\\Tim_STLx)

add_executable(MLP_BP main.cpp)

eigen小练手，图为两个矩阵相乘

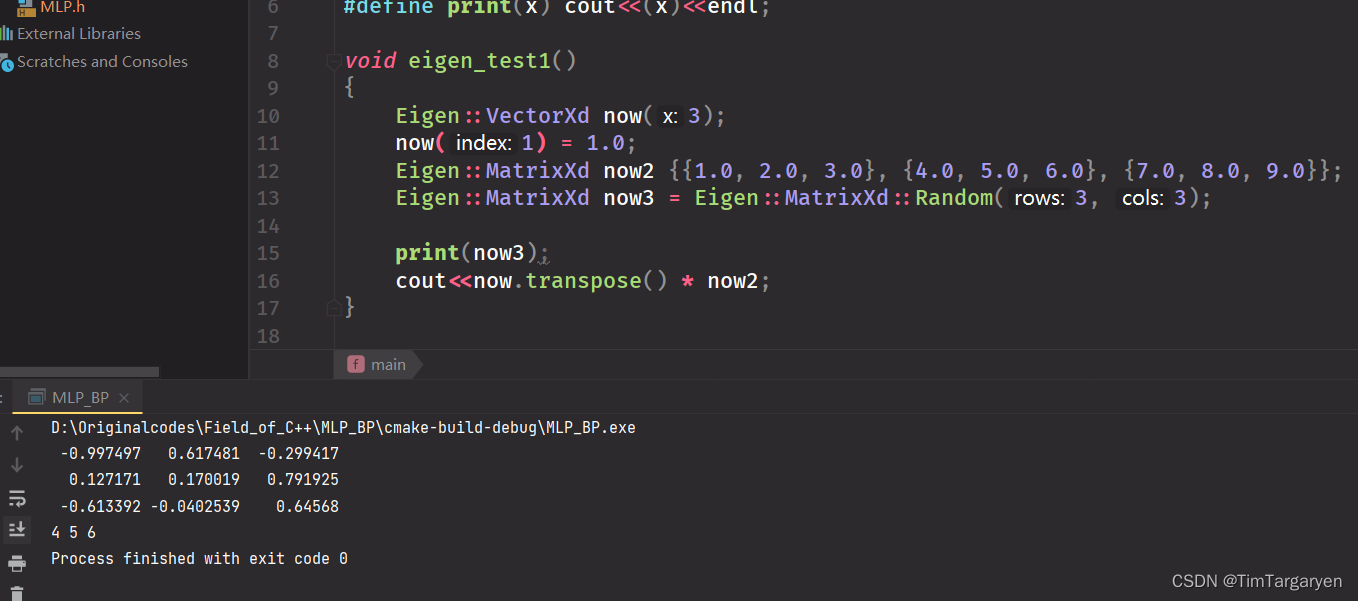
eigen很多有用的API

Eigen::VectorXd xxx;
Eigen::MatrixXd xxx;//人
xxx.resize(xx,xx,xx);
xxx.transpose();//转置
xxx.unaryExpr(lambda表达式);
xxx.binaryExpr(xx, lambda表达式)；
xxx<<1, 2, 3,
	4, 5, 6, 
	7, 8, 9;//输入矩阵

3. 原理上的一些推导

以下引自复旦邱锡鹏老师的nndl-book
手推（nndl-book自己进行了再推导）

一些点：
- 反向传播本质上是下一层的误差等于激活值的导数
- 最后一层的计算是通过直接把损失函数对最后一层的输入值也即未激活值进行求导，得到的是应该是向量，其他层都是对激活函数进行按位求导
- 因为反向传播的原因，实际上根本就没有对权重矩阵进行求导（如果不去bp的话），而是传换成了对激活函数求导 + 对上一层误差项的等价关系，然后就算出了权重矩阵的需要调整那个的变化量 $\Delta$
loss：从平均的二范数上衡量误差
bp算法是怎么work的？我的想法是高中就学过的链式法则的小量展开
激活函数的一些理解
- 最简单的:模拟神经元突触
- 对于多项式证明，我从思考过，定义一个激活函数对接受值非常敏感，从而模拟出指数的变化，有待下一步的实验进行证明
- 可以说，是激活函数在训练中权重矩阵的值进行了筛选，使所谓的pattern形成地更有区别

4.数据结构和实现的细节

容器选用的是我自己写的数据结构库Tim_STL中的list(毕竟是为了写cpp课设)，即链表的数据域中装载着神经网络的每个线性层
选择链表的原因是我的链表实现了正向与反向遍历（接受任意遍历器，模版加彷函数实现便历器），这和神经网络end2end的性质、前向推理与误差项反向传播优相当契合
求导的实现：选用的是较为简单的数值微分，即把函数当成一个黑盒，然后使用中心差分的方法去实现$ f’(x) = \frac{f(x + \Delta) - f(x - \Delta)}{2\Delta} $，人为的定义极小量，这里取的是$ \Delta = 0.0000001$

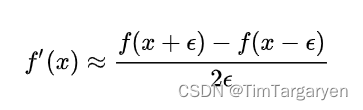
最关键的代码（实现的还不够优雅，乐）

前向传播

Eigen::VectorXd MLP::forward(Eigen::VectorXd const& x)
{
	auto temp = first();
	Eigen::VectorXd y = x;
	for (int i = 0; i < _size; i++, temp = temp->succ)
		y = temp->data(y);

	return temp->pred->data.a;
}

算最后一层的误差项

void SGD::set(Layer& layer)
{
	last_W = layer.W;
	error = Eigen::VectorXd::Random(layer.z.size());
	Eigen::VectorXd delta_z = layer.z;
	Eigen::VectorXd delta_z2 = layer.z;

	for (int i = 0; i < error.size(); i++) {
		delta_z[i] += delta;
		delta_z2[i] -= delta;
		double L = (loss(delta_z, Y) - loss(delta_z2, Y)) / (2 * delta);
		error[i] = L;
		delta_z[i] -= delta;
		delta_z2[i] += delta;
	}
}

反向传播，这里是把SGD当成遍历器

void SGD::operator()(Layer &layer)
{
	if (should) {
		set(layer);
		should = false;
	}
	else {
		Eigen::VectorXd delta_z = layer.z;
		Eigen::VectorXd delta_z2 = layer.z;
		for (auto& i: delta_z) i += delta;
		for (auto& i: delta_z2) i -= delta;
		delta_z.unaryExpr(layer.activate);
		delta_z2.unaryExpr(layer.activate);

		Eigen::VectorXd dadz = (delta_z - delta_z2).unaryExpr([](double x){return x / (2 * delta);});
		error = dadz.binaryExpr(last_W.transpose() * error, [](double x1, double x2){return x1 * x2;});
	}

	last_W = layer.W;
	layer.W -= LR * (error * layer.X.transpose() + regular_rate * layer.W);
	layer.B -= LR * error;
}

5. 实验

皆以预测值与真值间的相对误差$ Error = \frac{|\delta|}{S_{true}} $做为评价指标
线性回归，拟合的函数为$ F(X) = 4x_1 - 3x_2 + 2 x_1 + 10 $，选择的网络仅有单层三个神经元（以及一个bias）
- 一开始，可以看到损失函数下降的很快
- 最后的拟合结果，最后的avg_error也就是平均相对误差已经到10的-16次方了等于没有，打印的权重几乎一致
拟合一个任意的高次函数：$ F(X) = 6x_1^6 + 5x_2^5 + 4x_3^4 + 7x_4^7 + 2x_5^2$
- 数据分布：0 ~ 1内的正态分布
- 最后的训练结果，平均相对误差为1，预测值打印之后发现皆为0，很迷惑，为什么LOSS向着推理值横为0优化了？
- 打印最后的权重的初步结论是，权重基本作用于bias上跟输入都无关了，因为bias都很大，即我拟合了一个常值函数f(X) = 0

6. 下一步的挑战

思考为什么Loss会导向相对误差为0、预测值恒为0的状态？梯度爆炸？加skip connection会好吗？（我加过BN，没用）
这里我打算证明的是多项式情形即 $f(x_1, x_2, x_3, ..., x_n） = \prod_{i}^{m} (\sum_{j}^{n}a_{i, j}x_j)$ 其中的a可以从m层神经网络的权重矩阵中学得，当然这个
用ViT分patch的方式刷一下minst（pytorch采用LeNet架构可以刷到98%，目前sota99.4x），以及能不能用我的c++ MLP复现google 21年的工作MLP-mixer