本篇博文的矩阵展开都是根据状态向量为21维给出的,也就是位置误差、速度误差、失准角、陀螺常值零偏误差、加速度计常值零偏误差、陀螺比例因子误差、加速度计比例因子误差
卡尔曼滤波简介
概念
卡尔曼滤波算法作为一种重要的最优估计理论被广泛应用于各种领域,组合导航系统的设计是其成功应用中的一个最主要方面。卡尔曼滤波有离散型和连续型两种形式,前者可直接用于数字计算机上实现,后者更常用于卡尔曼滤波的理论性能分析。这里只介绍应用离散卡尔曼滤波算法实现GNSS/INS松组合解算的具体设计。

内容
在一个滤波周期内,卡尔曼滤波的信息更新过程可以分为时间更新过程和量测更新过程。其中时间更新又被称为预测,一步预测的状态及其协方差阵为:

方法

卡尔曼滤波器的初始化
GNSS/INS 松组合卡尔曼滤波算法设计的关键在于:建立离散时间系统误差状态模型,然后构建误差状态的线性观测方程。有了系统模型和观测方程则可直接使用卡尔曼滤波的基本方程进行组合导航解算,即完成了组合导航的算法设计。
系统状态
GNSS/INS 松组合常采用误差状态卡尔曼滤波(间接卡尔曼滤波)进行组合导航解算,以解决系统的非线性问题。因此,卡尔曼滤波的状态向量包含导航状态误差和传感器误差,定义为

微分方程

陀螺和加速度计零偏及比例因子误差均建模为一阶高斯马尔可夫过程


注意:系统噪声不能随意加入,而应该根据系统状态方程的推导式确定。例如位置误差微分方程中没有包含传感器误差,则一般情况下不应该在位置误差分量上加上系统噪声
离散化



GNSS 位置观测方程
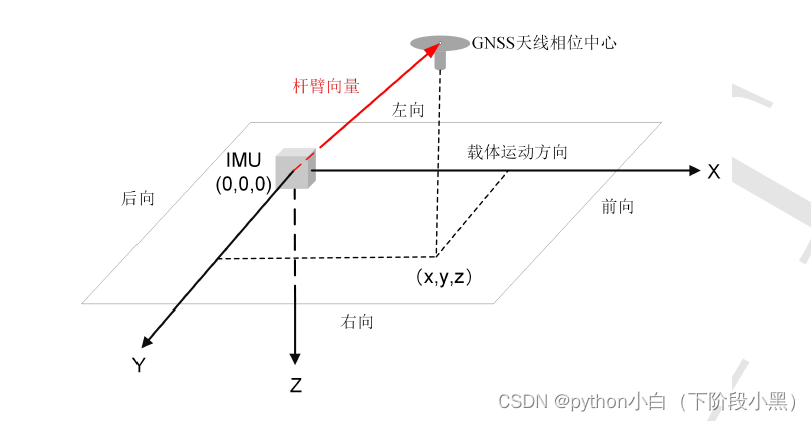
GNSS定位解算给出的是天线相位中心(或其它参考点)的位置坐标,INS机械编排给出的是IMU测量中心的导航结果,二者在物理上不重合((如图1所示),因此在数据融合解算时需进行杆臂效应改正。GNSS天线相位中心与 IMU测量中心之间的位置转换关系式为:





状态转移矩阵


系统噪声方差阵
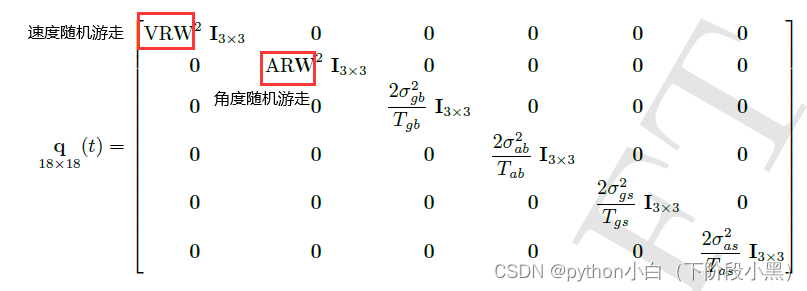
系统噪声驱动阵
