问题
三个物品他们的编号,重量和价值如下。1个背包能够称重30公斤,求装入的物品的最大价值
| 编号 | 重量 | 价值 |
|---|---|---|
| 1 | 16 | 45 |
| 2 | 15 | 25 |
| 3 | 15 | 25 |
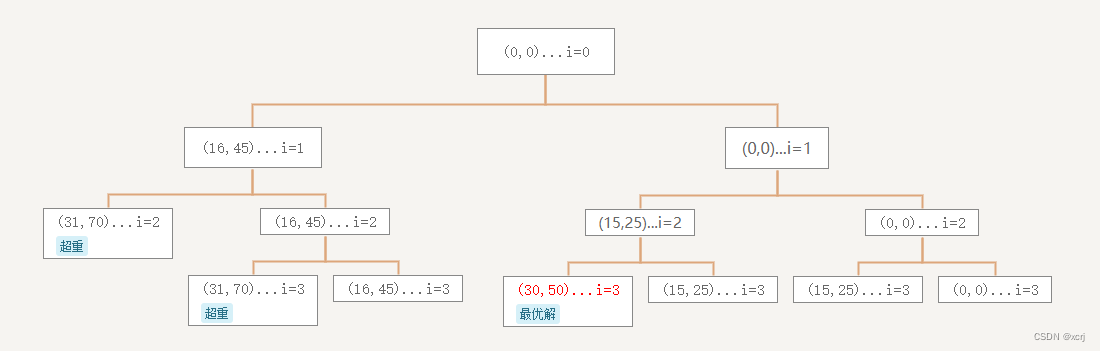
总结
广度优先搜索解空间树:结点是状态,分支是选择这个状态
- 一个物品产生两种状态(结点):加入状态,不加入状态
- 分支代表:你选择那种状态,你可以选择加入背包,也可以选择不加入背包
- 选择加入背包的条件:加入了不超重
- 选择不加入背包的条件:将来加入的物品更有价值
分枝:左分枝-加入背包,右分枝-不加入背包
限界:限界函数,限制走的分支,没有价值的分支不会往下走,走这个分支一定得不到解就不走
分枝限界法
分枝限界法:广度优先搜索解空间树
0. 解空间树:
- 左分枝代表选择,右分枝代表不选择
- 左孩子代表加入了第i个物品,右孩子代表没有加入第i个物品
- 选择不选择加入第i个物品:1~i-1物品重量之和+i物品重量<=背包可承受重量
- 活结点表:普通队列
- 限界函数:
- 当前结点是不是有前景的结点,从当前结点扩展下去能够获得更大价值
- 求最大价值是最大值问题,使用上界函数;当前结点的极大价值>当前最大价值,这个结点是有发展前景的结点,将这个结点放入活结点表
- 确定解向量的分量:
- 存储解向量的分量。例如,01背包问题的1个解的分量是选择的物品
- 当前结点包含的解向量,保存从根结点到该节点的路径
对比回溯法
| 回溯法 | 分枝限界法 |
|---|---|
| 回溯法使用栈进行DFS | 分枝限界法使用队列进行BFS |
| 回溯法可以找到所有解 | 分枝限界法只能找到1个解(最优解) |
| 回溯法所有结点都会被遍历 | 分枝限界法每个结点只有1次成为活结点的机会 |
代码
package xcrj.kchalgorithm.branchBound;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
/**
* 问题:
* 有n个物品 重量分别为{w1,w2,…,wn},价值分别为{v1,v2,…,vn}
* 背包能够承受的重量为w
* 选取一部分物品放入该背包
* 每个物品要么选中要么不选中
* 要求选中的物品不仅能够放到背包中,而且具有最大的价值
* <p>
* 分枝限界法对比回溯法:
* - 回溯法使用栈进行DFS,分枝限界法使用队列进行BFS
* - 回溯法可以找到所有解,分枝限界法只能找到1个解(最优解)
* - 回溯法所有结点都会被遍历,分枝限界法每个结点只有1次成为活结点的机会
* <p>
* 分枝限界法:广度优先搜索解空间树
* 0. 总结:
* - 首先是加入或不加入某个物品的两种状态,再是选不选择某个状态;选择不加入状态 看看剩下的的物品有没有更大价值(限界函数)-有更大价值就走,没更大价值就不走
广度优先搜索解空间树
* - 一个物品产生两种状态(结点):加入状态,不加入状态
* - 分支代表:你选择那种状态,你可以选择加入背包,也可以选择不加入背包
* - 选择加入背包的条件:加入了不超重
* - 选择不加入背包的条件:将来加入的物品更有价值
* 2. 限界函数:
* - 当前结点是不是有前景的结点,从当前结点扩展下去能够获得更大价值
* - 求最大价值是最大值问题,使用上界函数;当前结点的极大价值>当前最大价值,这个结点是有发展前景的结点,将这个结点放入活结点表
* 3. 确定解向量的分量:
* - 存储解向量的分量。例如,01背包问题的1个解的分量是选择的物品
* - 当前结点包含的解向量,保存从根结点到该节点的路径
*/
public class Knapsack {
/*解空间树结点类*/
static class Node {
// 第i个物品=第i层的物品(跟结点是第0层)
private int i;
// 结点编号
private int no;
// 结点总重量
private int weight;
// 结点总价值
private double value;
// 当前结点包含的解向量,保存从根结点到该节点的路径,xs[]数组元素值为1,表示取这个下标的元素,下标就是结点的唯一编号
private int[] xs = new int[n + 1];
// 上界价值
private double ubValue;
public Node() {
}
public Node(int i, int no, int weight, int value, int[] xs, double ubValue) {
this.i = i;
this.no = no;
this.weight = weight;
this.value = value;
this.xs = xs;
this.ubValue = ubValue;
}
}
/*问题描述*/
// 总物品数量=解空间树层级(层级从0开始)
private static int n = 3;
// 背包能够承受的重量
private static int availableWeight = 30;
// 每个物品的重量,下标0不使用,下标代表物品的唯一编号
private static int[] weights = {0, 16, 15, 15};
// 每个物品的价值,下标0不使用(根节点),下标代表物品的唯一编号
private static double[] values = {0, 45, 25, 25};
/*结果描述*/
// 最大价值
private static double maxValue = Double.MIN_VALUE;
// 最优解 选择哪些物品放进去
private static int[] opitimalXs = new int[n + 1];
// 解空间中结点总述,初始时1个结点A(0,0)
private static int tatalNode = 1;
/**
* !!!
* 价值上界函数,求每个结点的潜在价值(极大价值)
* 这个结点的极大价值>当前最大价值 证明从这个结点往后扩展结点能够获得更大价值,这个结点是有潜在价值的结点,有前景结点
* <p>
* 把背包装满,下一个物品不能全部装下了,打碎了也要把背包装满
*
* @param node 解空间树的结点
*/
public static void valueUpBound(Node node) {
// node结点的重量(包含了祖宗结点的重量)
int sumWeight = node.weight;
// node结点的价值(包含了祖宗结点的价值)
double sumValue = node.value;
// 准备处理下一层结点(孩子结点)
int i = node.i + 1;
// 尝试装入下一个物品
while (i <= n && (sumWeight + weights[i] <= availableWeight)) {
sumWeight += weights[i];
sumValue += values[i];
i++;
}
if (i <= n) { // 背包剩下的可承载重量 不能把下1个物品全部装入,
// 把剩下的物品打碎了装进去, (values[i] / weights[i])是单位重量价值
node.ubValue = sumValue + (availableWeight - sumWeight) * (values[i] / weights[i]);
} else {// 把所有物品都装下了,物品上界=总价值
node.ubValue = sumValue;
}
}
/**
* 解空间树结点放入队列
* 判断是否是叶子结点,叶子结点xs[]存储了一个解(自己+祖宗)
* - 到了叶子结点,处理这个可能解
* - 没有到叶子结点,结点入队
*/
public static void enQueue(Node node, Queue<Node> que) {
// 到了叶子结点,处理这个可能的解
if (node.i == n) {
// 注意,结点.value存储了自己和祖宗结点的价值之和
if (node.value > maxValue) {
maxValue = node.value;
// j从1开始到n结束,因为数组下标0没有使用
for (int j = 1; j <= n; j++) {
// 结点.xs[]中存储了自己和祖宗结点
opitimalXs[j] = node.xs[j];
}
}
} else {
// 非叶子结点,入队列
que.add(node);
}
}
/**
* 广度优先遍历
*/
public static void bfs() {
// 普通队列
Queue<Node> que = new LinkedList<>();
// 结点定义,3个物品,3个结点,node是根节点 ?
Node node = new Node();
node.i = 0;
// 根结点编号是1
node.no = tatalNode++;
node.value = 0.0;
for (int j = 1; j <= n; j++) node.xs[j] = 0;
// 根节点上界
valueUpBound(node);
// 根节点入队
que.add(node);
// 遍历根节点的下层子结点
while (!que.isEmpty()) {
// 出队1个结点
Node nodeHead = que.poll();
// 条件剪枝,当前结点的总重量+下个结点的重量 能放入背包时 才进行操作
if (nodeHead.weight + weights[nodeHead.i + 1] <= availableWeight) {
/*建立左孩子结点,选择第i个结点*/
Node nodeLeft = new Node();
nodeLeft.i = nodeHead.i + 1;
nodeLeft.no = tatalNode++;
nodeLeft.weight = nodeHead.weight + weights[nodeLeft.i];
nodeLeft.value = nodeHead.value + values[nodeLeft.i];
for (int j = 1; j <= n; j++) nodeLeft.xs[j] = nodeHead.xs[j];
nodeLeft.xs[nodeLeft.i] = 1;// xs[]数组元素值为1,表示取这个下标的元素,下标就是结点的唯一编号
// 节点上界
valueUpBound(nodeLeft);
// 节点入队
enQueue(nodeLeft, que);
}
/*建立右孩子结点,不选择第i个结点*/
Node nodeRight = new Node();
nodeRight.i = nodeHead.i + 1;
nodeRight.no = tatalNode++;
nodeRight.weight = nodeHead.weight;
nodeRight.value = nodeHead.value;
for (int j = 1; j <= n; j++) nodeRight.xs[j] = nodeHead.xs[j];
nodeRight.xs[nodeRight.i] = 0;// xs[]数组元素值为1,表示取这个下标的元素,下标就是结点的唯一编号
// 结点价值上界
valueUpBound(nodeRight);
// 剪枝,走右边,右结点是有前景的结点,背包能装入更有价值的物品;使用限界函数限制成为活结点;分枝限界法每个结点只有1次成为活结点的机会
if (nodeRight.ubValue > maxValue) {
// 节点入队
enQueue(nodeRight, que);
}
}
}
public static void main(String[] args) {
bfs();
System.out.println("最大价值:" + maxValue);
System.out.println("装入物品:" + Arrays.toString(opitimalXs));
}
}