文章目录
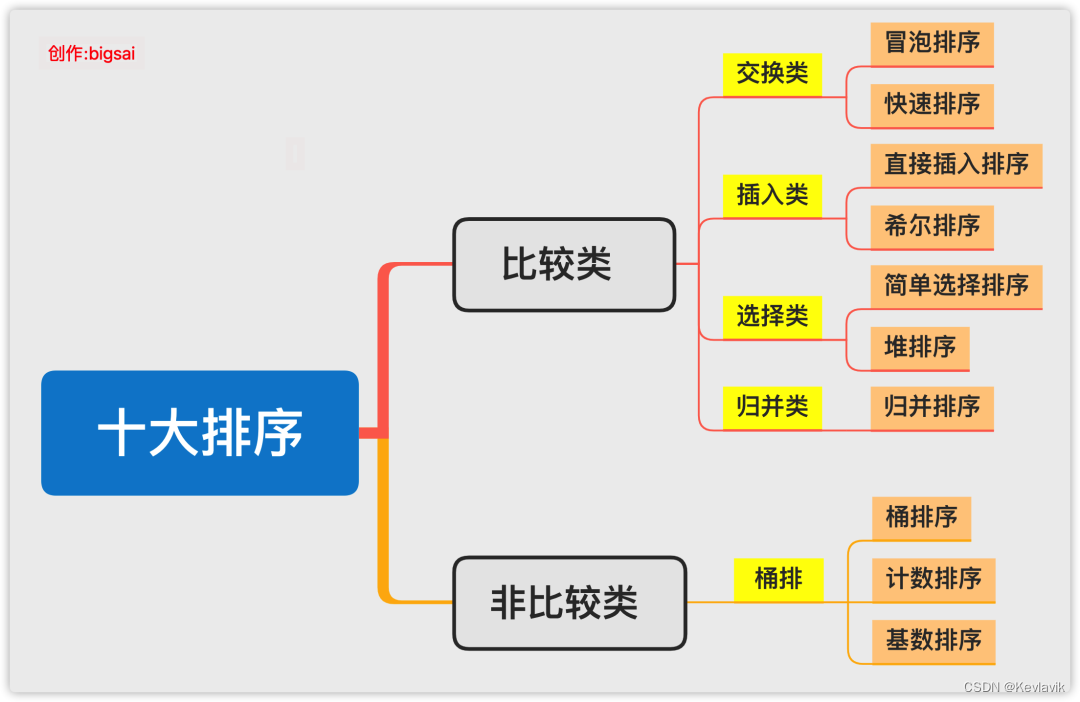
排序算法面试现状
知乎:邓卓…对排序算法的考察内容

升序为例
交换类
冒泡排序
中心思想…:每一个数从左向右依次比较,一趟下来确定一个最值放到最后,两个for循环
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n-i; i++)/跑完i躺 ,已经把i个大的数放到了最后,从前往后比的,所以不需要再比较了。
{
int flag = 1;
for (int j = 0; j < n - 1-i; j++)/不用再和i个已经比他大的数比较了
{
if (a[j] > a[j + 1])
{
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
flag = 0;
}
}
/一趟下来没有发生 交换说明俨然有序了
if (flag == 1)
{
return;
}
}
}
快速排序
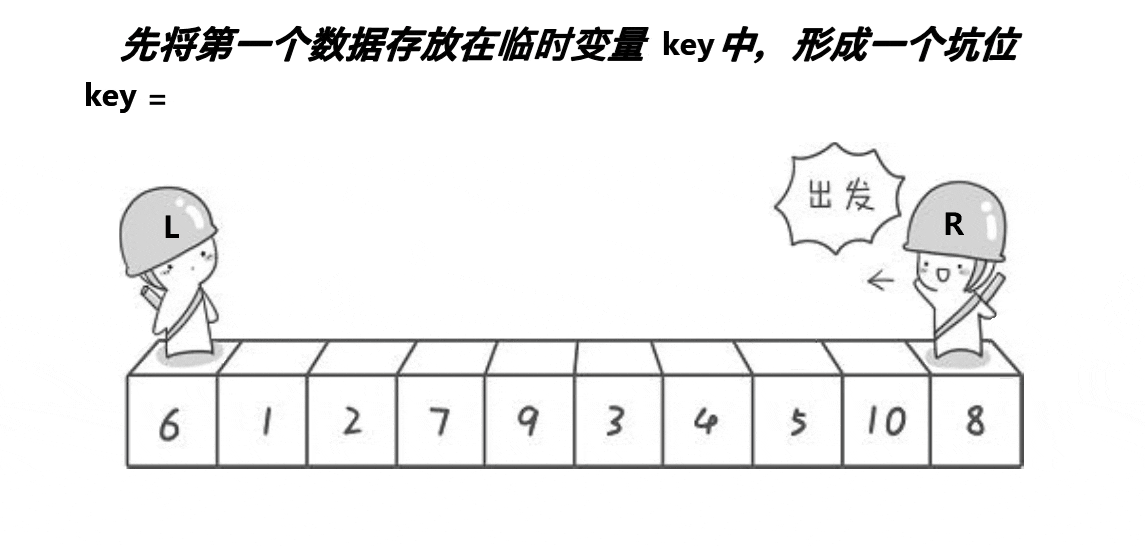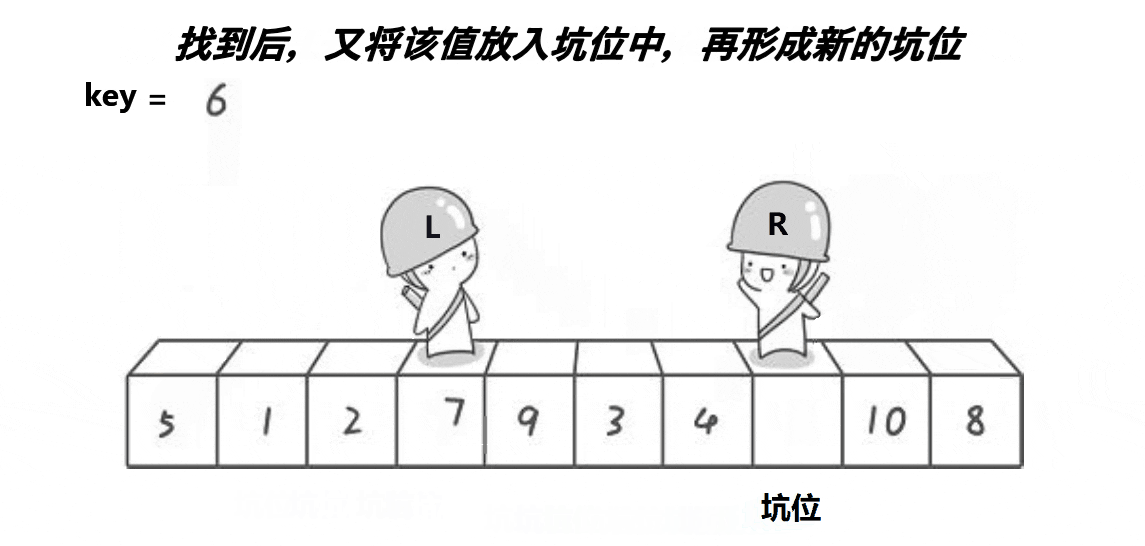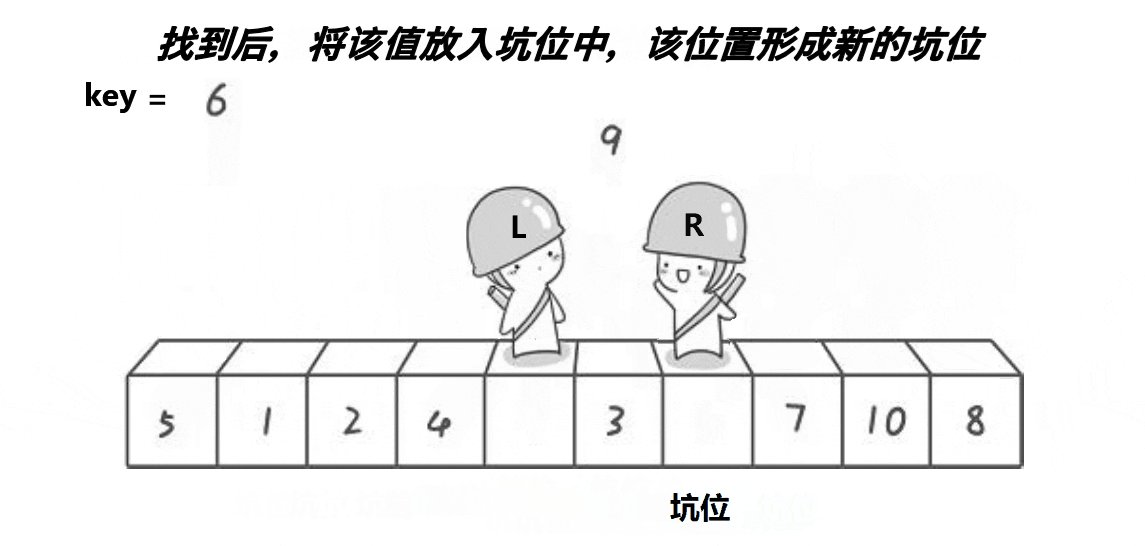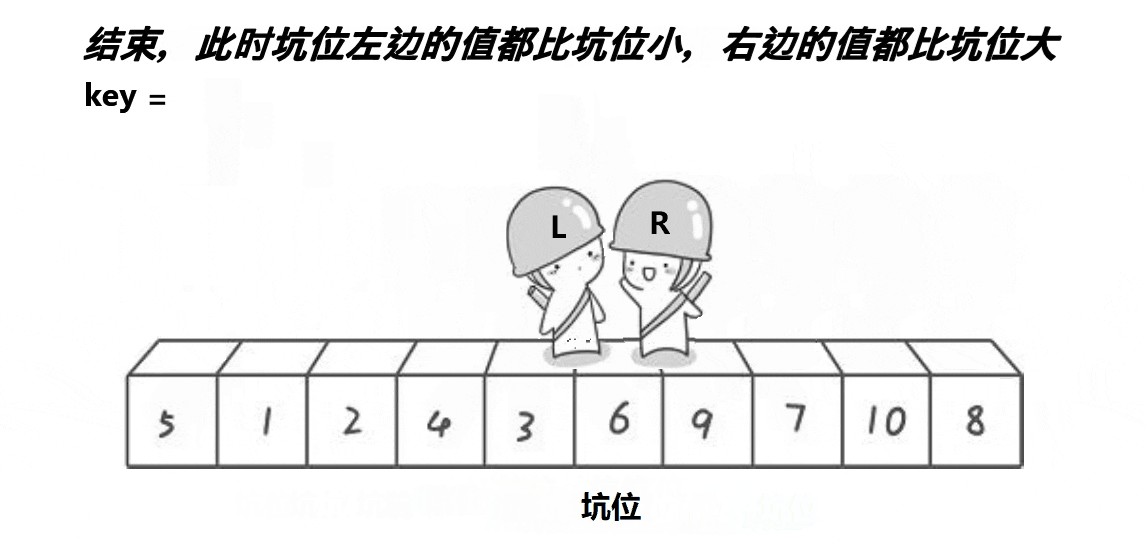
中心思想…:选定左边/右边第一个作为K值,从右往左找比它小的,从左往右找比他大的,交换;
相等停下,交换相等处值和K值,返回相等出的下标;
递归【left----K值下标】区间,和【K值下标----right】区间,直到【left>=right】return空
三数取中是在快速排序面对有序数组的神级优化插件,三个版本都可以用

快速排序1.0-原生hoare版本
三数取中
int ChooseKeysi(int*a, int left, int right)
{
/优化---针对接近高度有序的数组,接近于冒泡排序,因为高度有序,所以取头部,中间 尾部三个数比较
/选取一个合适 的作为基准值,便会大大加快快排面对有序数组的排序效率
int mid = left + (right - left) / 2;/防止左右坐标各自超过int的一半儿
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else //(a[left] > a[mid])
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
一趟快排
int PartSort(int* a, int left, int right)
{
int mid = ChooseKeysi(a, left, right);
/把左边的值换成基准值
swap(&a[mid], &a[left]);
int keys = left;
while (left<right)
{
/防止右边都是大的情况,一路减减,右边遇见了左,而左边还要一直加加
/右边找比k值小的, 如果一路没有小的便会和左边相遇,
while (left < right && a[right]>=a[keys])
{
--right;
}
/左边找比K值大的,和上面小的交换,脚底下就是小的了,
/相遇了就不会加加且该位置上就是小的数,就可以和K值换位置。把小的换到前面。
while (left < right && a[left]<=a[keys])
{
++left;
}
swap(&a[left], &a[right]);
}
/等于的地方便是K值最合适的地方,左右区间相对有序
/然后返回K值坐标,递归排序左右区间
/left停的地方必定是大的地方,然后和右边的小的互换。
swap(&a[keys], &a[left]);
return left;
}
多趟
void QuickS(int* a, int left, int right)
{
if (left>=right)
{
return;
}
int keyi = PartSort(a, left, right);
/对左右区间确定K值,当left == right 时,说明只有一个数了。
QuickS(a, left, keyi - 1);
QuickS(a, keyi + 1, right);
}
快速排序2.0-挖坑法
子函数2.0
int HoleSort(int* a, int left, int right)
{
int mid = ChooseKeysi(a, left, right);
/把左边的值换成基准值
swap(&a[mid], &a[left]);
int hole = left;
int k = a[hole];
while (left<right)
{
/右边开始走,把比key小的往洞里填
while (left < right && a[right]>= k)
{
--right;
}
/更新洞的坐标
a[hole] = a[right];
hole = right;
while (left < right && a[left]<=k)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = k;
return hole;
}
快速排序3.0-前后双指针法
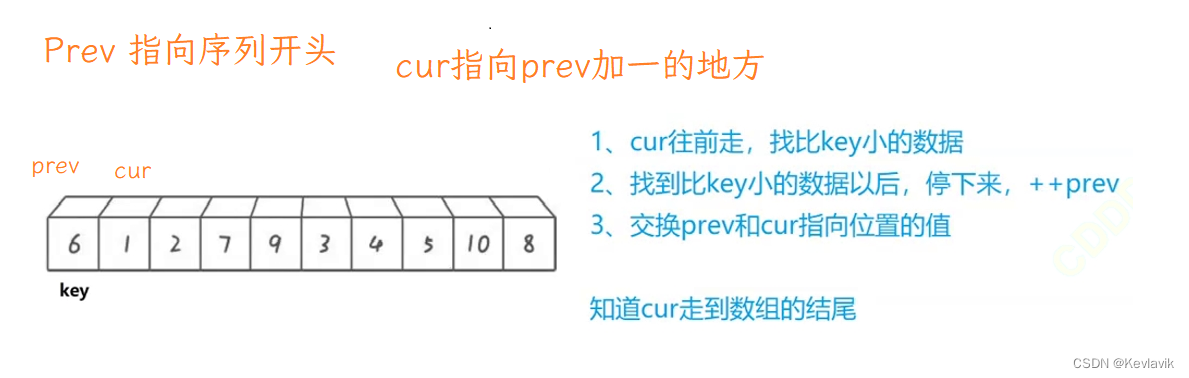

子函数3.0
int DoubleSort(int* a, int left, int right)
{
/把左边的值换成基准值
int mid = ChooseKeysi(a, left, right);
swap(&a[mid], &a[left]);
/Cur比prev多一,如果cur的值比k值小,则停下来,++prev,交换两个的值
/直至cur走到结束
int k = left;
int prev = left;
int cur = prev + 1;
while (cur<=right)
{
/防止一路都是小,一路原地交换
if (a[cur]<=a[k] && cur != ++prev)
{
swap(&a[prev], &a[cur]);
}
cur++;
}
swap(&a[prev], &a[k]);
return prev;
}
快速排序4.0-非递归版本
改造递归,用循环,或栈+循环
void QueickNoRecursion(int* a, int left, int right)
{
/需要初始化栈 入栈 出栈 栈顶元素,是否为空 ,栈的销毁
SK quc;
SKIinit(&quc);
/左右指针入栈,右边的先入
SKPush(&quc, right);
SKPush(&quc, left);
/记住每次要处理区间的左右下标,后进先出,栈不为空就处理
while (!SKEmy(&quc))
{
int lef = SKTop(&quc);
SKPop(&quc);
int rig = SKTop(&quc);
SKPop(&quc);
/基准值坐标
int k = DoubleSort(a, lef, rig);
/当k=左边右边时,说明待排序数组区间只剩一个了
/则下面不会执行,空栈了,循环结束。
if ( k<rig)
{
SKPush(&quc, rig);
SKPush(&quc, k+1);
}
if (lef<k)
{
SKPush(&quc, k - 1);
SKPush(&quc, lef);
}
}
SKDty(&quc);
}
插入类
直接插入排序
中心思想…:第一个坐标和后一个比,比他大则交换;第三个和前两个比较,放到合适的位置,以此类推形成相对有序,最后使整个数组有序,场景:打扑克牌
void InsertS(int* a, int n)
{
int i = 0;
for ( i = 0; i < n-1; i++) /i+1<=n-1
{
/假设前end个有序
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
希尔排序
中心思想…:一个叫希尔的人对直接插入排序的优化,将待排序数组分为gap组,每组间隔gap,对gap个间隔为gap的分组进行直接插入排序;等比缩小gap…当gap== 1时,数组接近有序

//希尔排序 O(N^1.3)...
void ShellS(int* a, int n)
{
int gap = n;
while (gap>1)
{
/分组
/ 2/3=0 +1
gap = gap / 3 + 1;
/对多个分组同时进行直接插入排序
for (int i = 0; i < n - gap; i++)//i+gap<n
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
/确保前end个有序
end -= gap;
}
else
{
break;
}
}
/0-gap = -gap
a[end + gap] = tmp;
}
}
}
选择类
简单选择排序
中心思想…:每一趟选出一个最值,放到起始位置…
void SelectS(int* a, int n)
{
int begin = 0;
int end = n - 1;
int min = begin;
int max = begin;
while (begin<end)
{
/选出遍历一遍,选出整个数组最大最小的
for (int i = begin; i <=end ; i++)
{
if (a[begin] < a[min])
{
min = begin;
}
if (a[begin] > a[max])
{
max = begin;
}
}
/最大的放尾部,最小的放头部,同时缩减数组比较范围
swap(&a[begin], &a[min]);
if (begin == max)
{
/假设最大的是头部,换完之后,最大的跑到了min那里
max = min;
}
swap(&a[end], &a[max]);
begin++;
end--;
}
}
堆排序
中心思想…:找到最后一个非叶子节点,进行向下调整算法,减减到0为止。
归并类
中心思想…:似与二叉树的前序遍历,需要将左右区间相对有序,再将整体有序;
分区间取值排序(left—mid;mid—right),放进临时数组,再将临时数组拷贝给原数组;
非递归版分成2的次方倍的gap组进行归并…
归并排序1.0-递归版
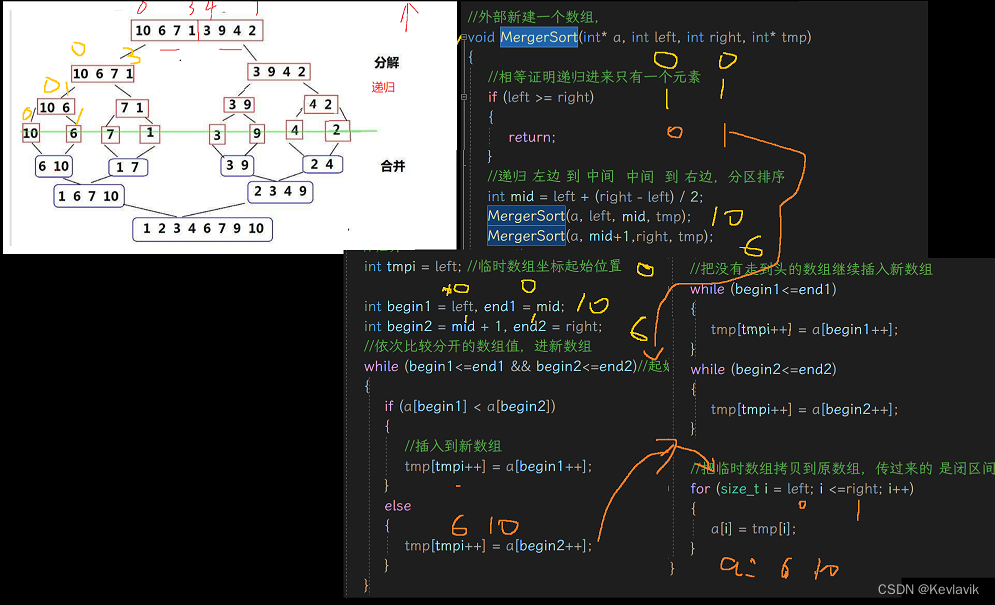
void MergerSort(int* a, int left, int right, int* tmp)
{
/相等证明递归进来只有一个元素
if (left >= right)
{
return;
}
/递归 左边 到 中间 中间 到 右边,分区排序
int mid = left + (right - left) / 2;
MergerSort(a, left, mid, tmp);
MergerSort(a, mid+1,right, tmp);
/归并
int tmpi = left; /临时数组坐标起始位置
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
/依次比较分开的数组值,进新数组
while (begin1<=end1 && begin2<=end2)/起始坐标小于等于数组尾部坐标结束
{
if (a[begin1] < a[begin2])
{
/插入到新数组
tmp[tmpi++] = a[begin1++];
}
else
{
tmp[tmpi++] = a[begin2++];
}
}
/把没有走到头的数组继续插入新数组
while (begin1<=end1)
{
tmp[tmpi++] = a[begin1++];
}
while (begin2<=end2)
{
tmp[tmpi++] = a[begin2++];
}
/临时数组拷贝到原数组,传过来的是闭区间
for (int i = left; i <=right; i++)
{
a[i] = tmp[i];
}
}
归并排序2.0-非递归版
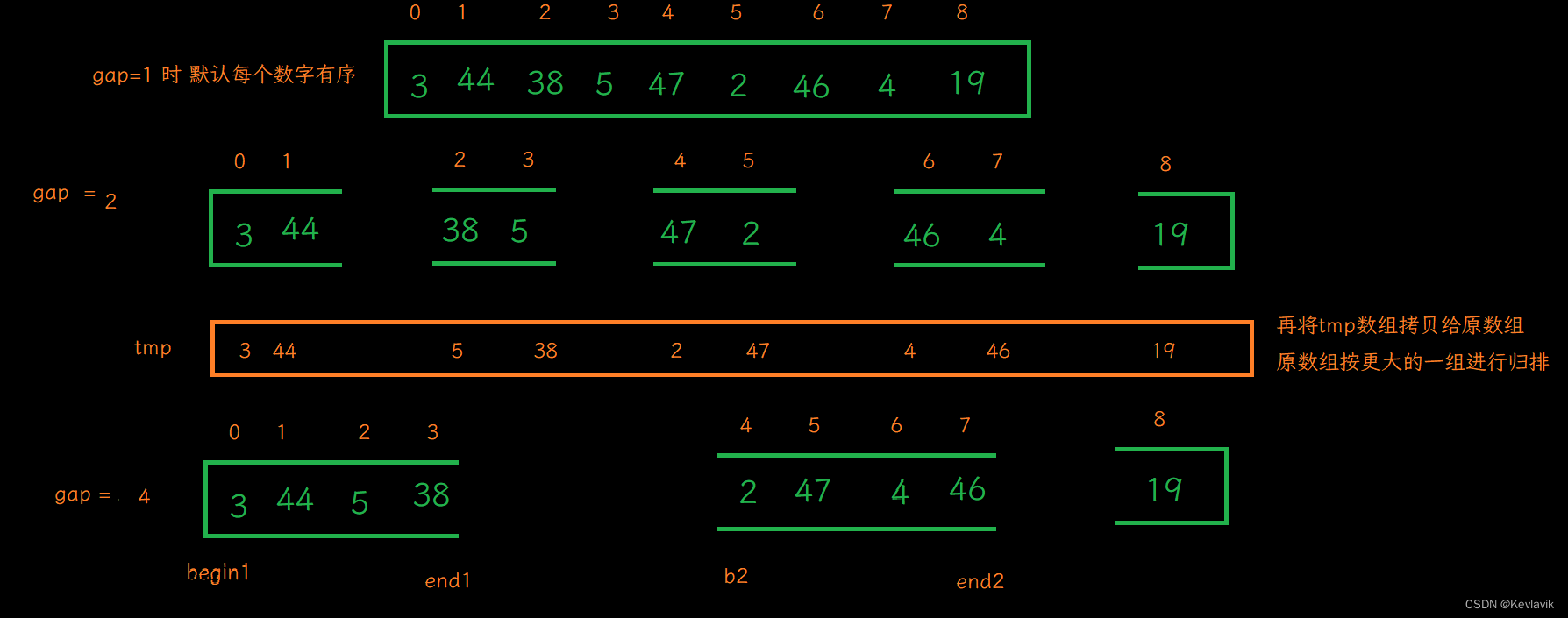
void MergerSortNoRe(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
/将递归改为循坏, 依次分成1 2 4 8... 组 归并排序
int gap = 1;
while (gap<n)
{
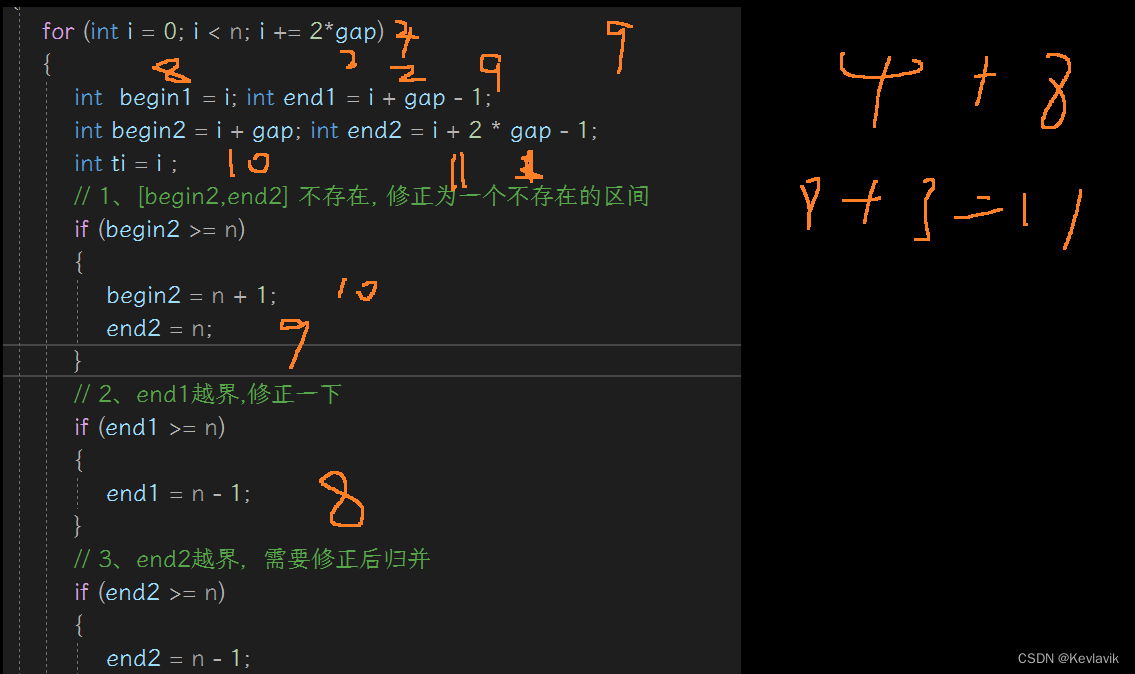
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i; int end1 = i + gap - 1;
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
int ti = i ;
/ 1、[begin2,end2] 不存在, 修正为一个不存在的区间
/下面while 的 b2 <=end2 就不会生效,,end 1越界 begin2就会越界
if (begin2 >= n)
{
begin2 = n + 1;
end2 = n;
}
/ 2、end1越界,修正一下, gap 4 i = 8 e1 =11 数组9
if (end1 >= n)
{
end1 = n - 1;//8
}
/ 3、end2越界,需要修正后归并 gap 2 i=6 b2 = 8 e2= 11
if (end2 >= n)
{
end2 = n - 1;// b2 8 end2 8 19
}
while (begin1 <= end1 && begin2 <= end2) //b1 0 end1 7 8 8 19
{
/取小值放入临时数组
if (a[begin1]<a[begin2])
{
tmp[ti++] = a[begin1++];
}
else
{
tmp[ti++] = a[begin2++];
}
}
/有一个越界,一个还没比较完,则将还没比较完的给临时数组
while (begin1 <= end1)
{
tmp[ti++] = a[begin1++];/b1 8 end1 7 ti 8 ti++= 9 上面结束
}
while (begin2 <= end2)
{
tmp[ti++] = a[begin2++];
}
}/将分成多组的每两组都进行比较,导入临时数组
/进行下一次调整分组前将临时数组导入给原数组
for (int i = 0; i < n; i++)
{
a[i] = tmp[i];
}
gap *= 2;
//SortPrint(a,9);
}
}
非比较类:计数排序
中心思想…:相对映射,原数组的值减去最小值作为临时数组的下标;临时数组下标位置统计原数组值出现的次数;最后根据临时数组的次数,将临时下标加上最小值返给原数组
1.计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
void ConutSort(int* a, int n)
{
int i = 0;
int max = a[0], min = a[0];
for ( i = 1; i < n; i++)
{
if (a[i]>max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
} /相对映射,绝对映射,决定开辟的临时数组的大小
/相对映射 ,数组的最大值 -- 最小值
int tmpn = max - min+1;//40-20 21个数
int* tmp = (int*)calloc(tmpn, sizeof(int));
/原数组元素减去一个最小值 是tmp数组的坐标,相同的值会有相同的坐标
/tmp元素记录 该值 出现的次数
for ( i = 0; i < n; i++)
{
tmp[a[i] - min]++;
}
//tmp坐标
int j = 0;
i = 0;
for ( j = 0; j < tmpn; j++)
{
while (tmp[j]--)/值出现的次数
{
a[i++] = j + min; /下标加上最小值 还原元素
}
}
free(tmp);
}
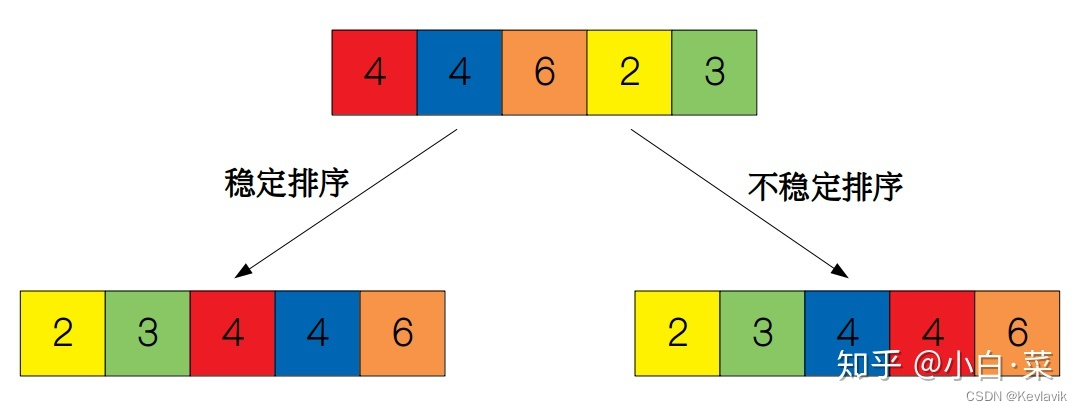
排序算法稳定性的意义
中心思想…:本来想等的两个值,他在前,她在后,排完序后相对位置不变;场景之一:发奖金
原始稳定的有 : 冒泡,直接插入.归并;但都可以写成不稳定
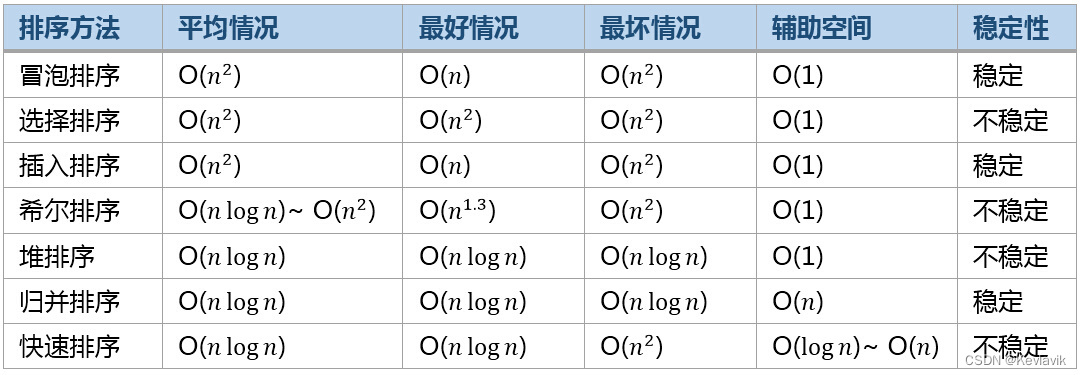
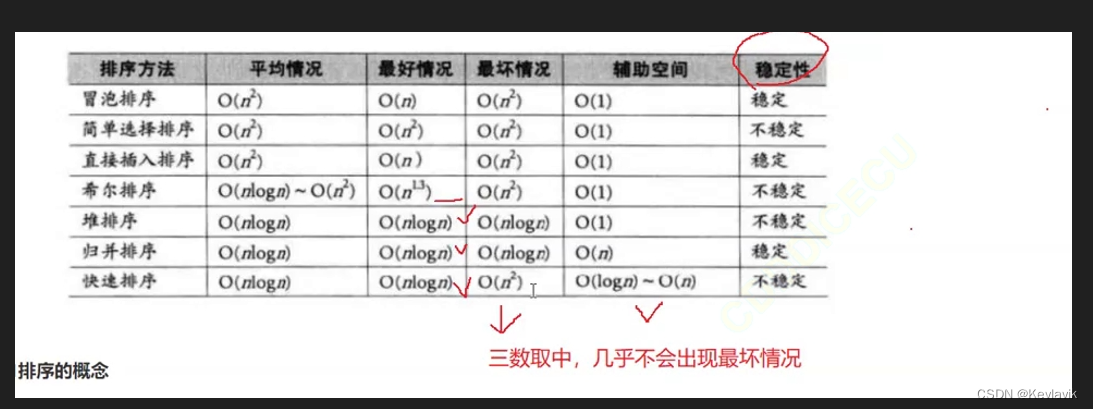
各算法的时空间复杂度
中心思想…:第一梯队:快速排序,堆排序,归并排序,平均都是(N*logN)…
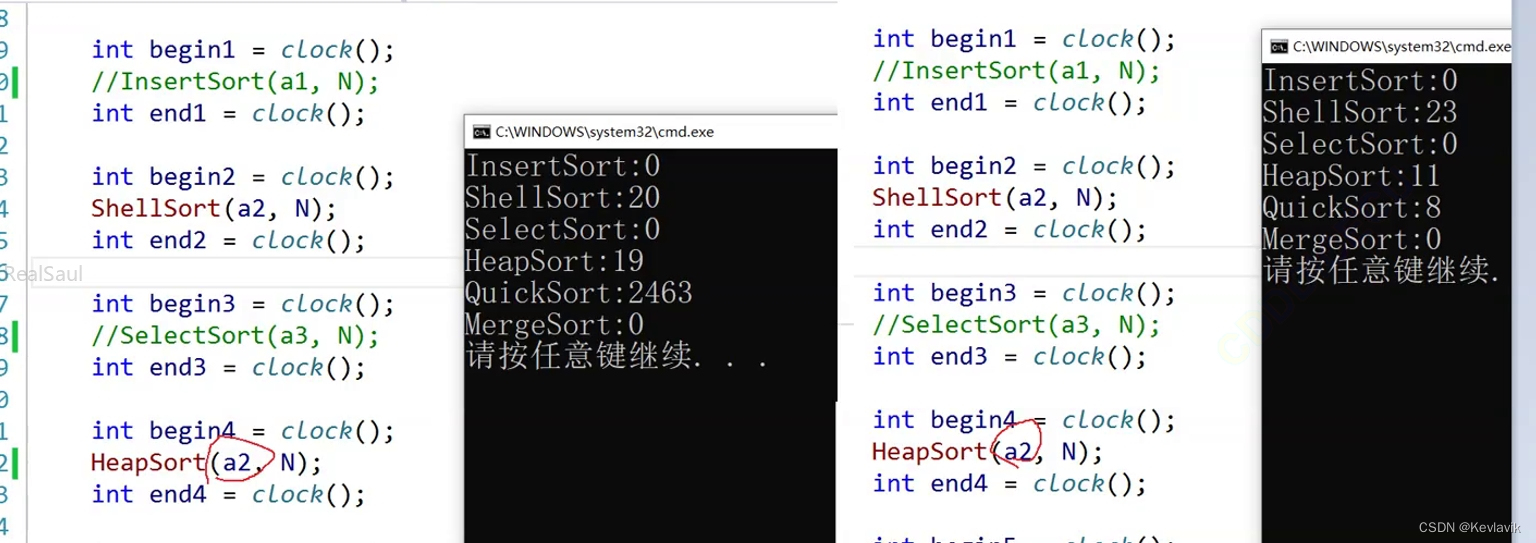
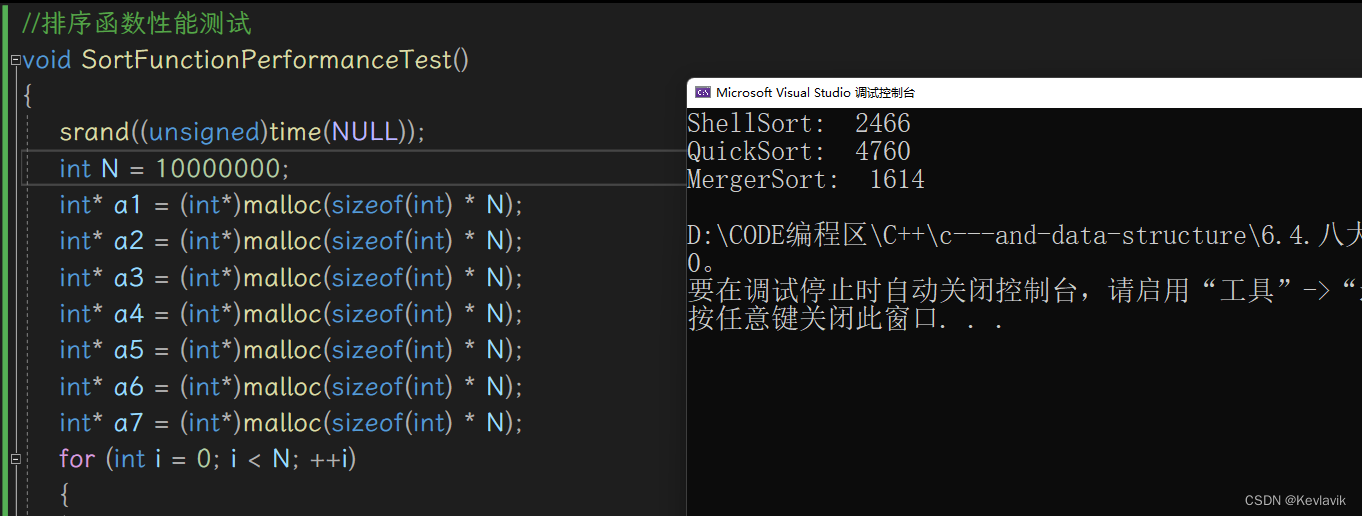
各算法性能测试
/排序函数性能测试
void SortFunctionPerformanceTest()
{
srand((unsigned)time(NULL));
int N = 100000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
//int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
//int* a6 = (int*)malloc(sizeof(int) * N);
//int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
//a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
//a6[i] = a1[i];
//a7[i] = a1[i];
}
//int start1 = clock();
//InsertS(a1, N);
//int end1 = clock();
int start2 = clock();
ShellS(a2, N);
int end2 = clock();
//int start3 = clock();
//SelectS(a3, N);
//int end3 = clock();
int start4 = clock();
QuickS(a4, 0, N - 1);
int end4 = clock();
int* tmp = (int*)malloc(N * sizeof(int));
int start5 = clock();
MergerSort(a5, 0, N - 1, tmp);
int end5 = clock();
//int start6 = clock();
//ConutSort(a6,N);
//int end6 = clock();
//int start7 = clock();
//BubbleSort(a7, N);
//int end7 = clock();
//printf("InsertSort: %d\n", end1 - start1);
printf("ShellSort: %d\n", end2 - start2);
//printf("SelectSort: %d\n", end3 - start3);
printf("QuickSort: %d\n", end4 - start4);
printf("MergerSort: %d\n", end5 - start5);
/printf("CountSort: %d\n", end6 - start6);
/*printf("BubbleSort: %d\n", end7 - start7);*/
free(a1);
free(tmp);
free(a2);
/free(a3);
free(a4);
free(a5);
/free(a6);
/free(a7);
}
我的快排可能有问题…
递归程序的问题

编者寄语
秉持着自己写的代码,只有自己看的懂的原则…hhh,单链表专训练,二叉树专题训练,大复习作业…