在大城市,地铁系统对于游客来说总是看起来如此复杂。
为了使你对此有所了解,下图显示了北京地铁的地图。
现在,请你帮助编写一个程序,给定用户的起始位置,找到到达其目的地的最快方法。
输入格式
第一行包含一个正整数 N,表示地铁线路的数量。接下来 N 行,第 i 行以下列格式描述第 i 条线路(地铁线路都是双向的):
M S[1] S[2] ... S[M]
其中 M 是站点数量,S[i] 是沿线站点的编号(站点编号是从 0000 到 9999 的 4 位数字)。
确保这些站点是按照地铁行进顺序给出的,即地铁会从 S[i] 直接开到 S[i+1]。
注意,可能会存在回路,但不存在自环(即地铁从 S 出发,直接开向 S,中途不经过任何站点)。
每个车站间隔都只属于一条唯一线路。
一些线路可能会在某些站点(中转站)彼此交叉,但是不能有任何站点作为中转站时,有超过 5 条线路在该站点交汇。
描述完地铁线路信息后,包含一行整数 K,表示询问次数。
接下来 K 行,每行描述一个询问,包含两个站点编号分别表示始发站和目的地。
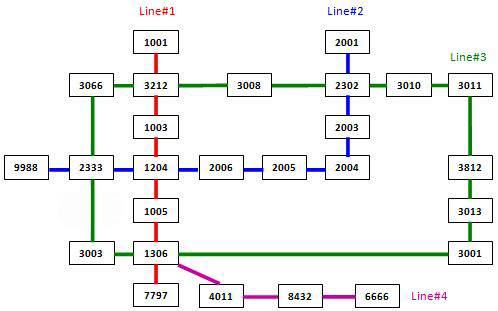
下面是示例图:
保证所有站点都能到达,询问站点编号合法。
输出格式
对于每个询问,首先输出最少需要停靠的站点数量,然后以如下格式输出最佳线路:Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
......
其中 Xi 是线路编号,Si 是站点编号,除始发站和终点站外,只输出中转站。如果最快线路不唯一,则输出换乘次数最少的线路,保证唯一。
数据范围
1≤N≤100,
1≤M≤100,
1≤K≤10
输入样例:
4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
3
3011 3013
6666 2001
2004 3001
输出样例:
2
Take Line#3 from 3011 to 3013.
10
Take Line#4 from 6666 to 1306.
Take Line#3 from 1306 to 2302.
Take Line#2 from 2302 to 2001.
6
Take Line#2 from 2004 to 1204.
Take Line#1 from 1204 to 1306.
Take Line#3 from 1306 to 3001.
我的解法:
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 1000010;
typedef pair<int, int> PII;
int n, stops[N];
int e[M], ne[M], w[M], h[N], idx;
int line[M];
int dist[N], pre[N];
bool st[N]; // 由于是无向图,所以要记录节点是否被使用过
int cnt[N]; // 记录换乘次数
string info[N]; // 记录乘坐信息
void add(int a, int b, int c, int id){
e[idx] = b, w[idx] = c, line[idx] = id, ne[idx] = h[a], h[a] = idx ++;
}
string to_build(int n){
string s = to_string(n);
while(s.size() != 4){
s = "0" + s;
}
return s;
}
void dijkstra(int start, int end){
memset(dist, 0x3f, sizeof dist);
memset(cnt, 0x3f, sizeof cnt);
memset(st, 0, sizeof st);
priority_queue <PII, vector<PII>, greater<PII>> heap; // 堆维护迪杰斯特拉算法
dist[start] = cnt[start] = 0;
heap.push({0, start});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second;
if (ver == end) break;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i]; // 找到节点名字
if(dist[j] > dist[ver] + w[i]){ // 说明要换乘了
dist[j] = dist[ver] + w[i];
cnt[j] = cnt[ver] + 1;
pre[j] = ver;
info[j] = "Take Line#" + to_string(line[i]) + " from " +
to_build(ver) +" to " + to_build(j) + ".";
heap.push({dist[j], j});
}
else if(dist[j] == dist[ver] + w[i]){
if(cnt[j] > cnt[ver] + 1){
cnt[j] = cnt[ver] + 1;
pre[j] = ver;
info[j] = "Take Line#" + to_string(line[i]) + " from " +
to_build(ver) +" to " + to_build(j) + ".";
}
}
}
}
cout << dist[end] << endl;
vector <string> path;
for(int i = end; i != start; i = pre[i]){
path.push_back(info[i]);
}
for(int i = path.size() - 1; i >= 0; i -- ){
cout << path[i] << endl;
}
}
int main(){
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++ ){
int m;
cin >> m;
for(int j = 0; j < m; j ++ ) cin >> stops[j];
for(int j = 0; j < m; j ++ ){
for(int k = 0; k < j; k ++ ){
int len;
if(stops[0] != stops[m - 1]) len = j - k;
else len = min(j - k, m - 1 - j + k);
add(stops[j], stops[k], len, i); // 创建邻接表按照车站名创建
add(stops[k], stops[j], len, i);
}
}
}
int k;
cin >> k;
while(k --){
int start, end;
cin >> start >> end;
dijkstra(start, end);
}
return 0;
}堆优化版迪杰斯特拉算法,适用于图中边数较多的情况
模板例题:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 ?1。
输入格式
第一行包含整数 n 和 m。接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。如果路径不存在,则输出 ?1。
数据范围
1≤n,m≤1.5×105,
图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 109。输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
模板:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef pair<int, int> PII;
int h[N], ne[N], w[N], e[N], idx;
int dist[N];
bool st[N];
int n, m;
void add(int a, int b, int c){
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dijkstra(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while(heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second;
if(st[ver]) continue;
st[ver] = true;
for(int i = h[ver]; i != -1; i = ne[i]){
int j = e[i];
if(dist[j] > dist[ver] + w[i]){
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main(){
memset(h, -1, sizeof h);
cin >> n >> m;
while(m --){
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}收获:
使用c++的优先队列stl来模拟堆,即priority_queue
优先队列具有队列的所有特性,包括基本操作,只是在这基础上添加了内部的一个排序,它本质是一个堆实现的
和队列基本操作相同:
top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容
定义:priority_queue<Type, Container, Functional>
Type 就是数据类型,Container 就是容器类型(Container必须是用数组实现的容器,比如vector,deque等等,但不能用 list。STL里面默认用的是vector),Functional 就是比较的方式,当需要用自定义的数据类型时才需要传入这三个参数,使用基本数据类型时,只需要传入数据类型,默认是大顶堆
为了方便解题,可以根据题意自己额外建边