[数据结构与算法]Automatic Mapping of Tailored Landmark Representations for Automated Driving and Map Learning 论文阅读

ICRA 2021 论文链接
源代码 无

1 速读

1.1 论文试图解决什么问题？这是否是一个新的问题？

高精度地图的高维语义信息（mask）的自动构建问题；是个较新的问题，没有被广泛的解决，问题在于高维度的表示和高成本中间的矛盾；
用途为对交通语义信息自动构建，从人力操作转化为程序自动构建+人工修正误检测；

1.2 有哪些相关研究？如何归类？谁是这一课题在领域内值得关注的研究员？

各种语义目标的构建方法；object SLAM中的表示；

1.3 文章的贡献是什么？

利用雷达给出的深度和朝向+语义信息，解决了单目情况下的地图语义元素的检测+追踪+建图这一整套流程；
对交通标识+交通灯+杆子建模，定位精度<10cm，大小精度<5cm，朝向MAE<6°；
①对语义用精简的方式建模；
②语义信息+雷达数据从单帧中恢复语义目标的而深度和朝向；
③data association方法；
④多视角landmark估计方法；

1.4 文章解决方案的关键是什么

1.5 实验如何设计？实验结果足够论证其效果吗？

没有合适的benchmark，无法推广到KITTI数据集，所以用自己的车测量了三个具有挑战性的数据；
采集车配置：4096 × 1536 pixels that is triggered with 10 Hz when the Velodyne VLS-128 Alpha Prime lidar；
Single Measurement Precision：单帧测量准确度，应该是只用雷达信息+一帧信息恢复，为了说明单帧测量的精度很高满足使用需求；
Map Optimization Results：

1.6 数据集是什么？

1.7 还会存在什么问题

作者conclution：
1.将语义信息和位姿一同优化
我觉得：
2.其他道路信息怎么办？
3.没有合适的benchmark

2 主要内容

2.1 系统框架

整个思路有点像SfM，通过点云流和视频流恢复场景中的路标，路灯，路杆等信息；
①预处理得到需要的信息；
②滤除不好的数据并利用雷达测量做深度估计；
③恢复出语义的参数化表示；
④进行帧间关联，并优化地图信息；

2.2 参数化

2.2.1 预处理

语义网络得到mask和bounding box+视觉SLAM系统得到准确位姿；
得到：语义测量${\mathcal{D}}_k$，类别标签$c_m$，bounding box左上和右下的图像坐标$d_{TL/BR}^m$，雷达点云${\mathcal{L}}_k$，每帧的位姿$T_k$;

2.2.2 pre-filtering

①过滤掉重复检测到的landmarks，bounding box的IoU>10%就是重复（这阈值也太低了吧？）；
②bounding box需要足够优秀，mask占据bounding box的比例>30%;

2.2.3 深度估计

雷达点云投影到像素平面并结合mask得到深度；
由于雷达和相机的安装位置不完全相同，所以两者观测到的东西不会完全相同，如下图所示：路牌上有来自后方汽车的点云信息，是因为在雷达的位置可以绕过路牌探测到后方车辆，但是投影到像素平面被认为是路牌的深度了；

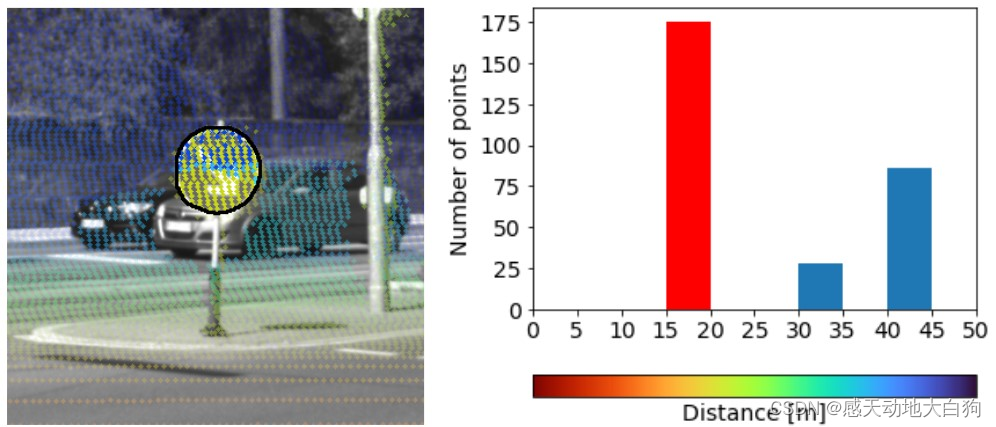
解决方法为利用DBSCAN algorithm对雷达点云进行聚类，在投影时只关注具有最近距离的那个聚类点云的数据；

2.2.4 参数表示

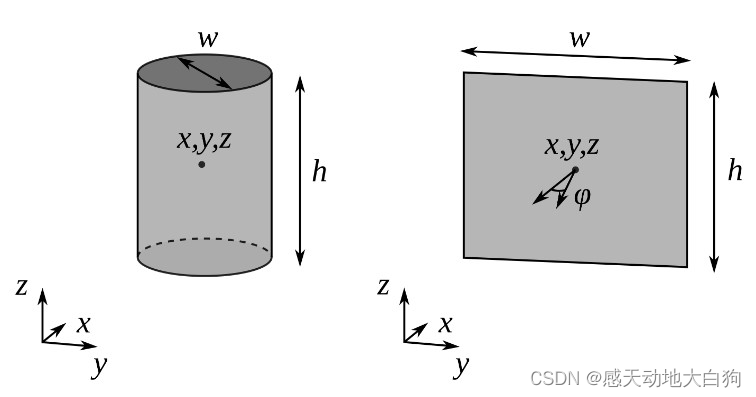
路杆、路灯：直立部分用圆柱体表示：位置xyz，宽w，高h；
标志：用方框表示：位置xyz，宽w，高h，多了一个z方向的朝向角$\phi$;

①求解点云中心$x_{\mathcal{L}}$：
$$x_{\mathcal{L},\theta }=\underset{x_{\mathcal{L},\theta }}{\mathrm{argmin}}\sum _{l_i\in {\mathcal{L}}_k^m}\rho (||l_{i,\theta }?x_{\mathcal{L},\theta }|{|}^2)$$②将点云中心$x_{\mathcal{L}}$投影到观测方向$d_C$上得到真正的中心$x$（这个思想对构建object很有帮助！！）：
这样做是因为：
首先，观测到的点云肯定是真实物体的一个侧面，无法正确描述物有轮廓物体的空间位置；
其次，物体的真实中心很可能在2d bounding box的中心所在的投影方向上；
这样即可通过投影方向+点云中心两个条件大致确定物体的中心了，如下图：

图中的平面表示垂直于地面，过$x_{\mathcal{L}}$的平面，法向量可以通过观测方向的投影确定：
$$n=d_G=\frac{1}{\sqrt{d_{C,1}^2+d_{C,2}^2}}?\begin{array}{c}{d}_{C,1}\\ d_{C,2}\\ 0\end{array}?$$
根据法向量可以确定中心$x$：
$$x=\frac{x_{{\mathcal{L}}^T}?n}{{d_C}^T?n}{d}_C=\frac{x_{{\mathcal{L}}^T}?d_G}{{d_C}^T?d_G}{d}_C$$
③长宽wh确定，根据bounding box和平面的交点坐标确定；
交通灯和路杆：
$$x_{TL/BR}=\frac{x^T?d_G}{d_{TL/BR}^T?d_G}=d_{TL/BR}$$
标志：其中$n_{\mathcal{L}}$是由点云拟合的平面向量
$$x_{TL/BR}=\frac{x^T?n_{\mathcal{L}}}{d_{TL/BR}^T?n_{\mathcal{L}}}=d_{TL/BR}$$
标志还多一个朝向角，通过地面法向量计算：
$$\phi =arccos(?d_D^T?n_{\mathcal{L}})$$
得到bounding box在空间中的坐标后可用这些坐标来计算wh；

2.2.5 bounding box测量

较远处的object由于雷达测量点稀疏，对bounding box中少于5个雷达投影的情况，只用该bounding box去优化中心$x$；
2.3 数据关联
由于雷达在近处表现更好，所以选择时间上倒序的方式（倒退行驶），匹配策略采用匈牙利算法；
2.4 地图优化
从所有恢复的landmark中计算出最有的结果，做法是每有一个新关键就优化一次地图（为了更好地实现匹配）
所谓地图优化即从所有结果中算一个代价最小的：参数为 θ ∈ { x , y , z , w , , h , φ } \theta\in\{x,y,z,w,,h,\varphi\} θ∈{x,y,z,w,,h,φ};
$${\widehat{?}}_{i,\theta }=\underset{{?}_{i,\theta }}{\mathrm{argmin}}\sum _{p_i\in {\mathcal{A}}_{{\widehat{?}}_i}}\rho (||{?}_{i,\theta }?p_{j,\theta }|{|}^2)$$