1 引言

自动驾驶仪的核心任务是保证导弹精确、鲁棒的跟踪制导系统生成的输入指令，使导弹稳定的飞行直至命中目标。在战术导弹控制领域，过载驾驶仪扮演着非常重要的角色；常见的过载驾驶仪有经典两回路过载驾驶仪、带 PI 校正的两回路过载驾驶仪、经典三回路过载驾驶仪、伪攻角反馈三回路过载驾驶仪等。采用线性二次型最优控制理论进行自动驾驶仪设计，不仅使设计出的驾驶仪有一定的稳定裕度，而且在求出最优控制时，也推导出了对应的自动驾驶仪结构，即可从最优控制理论的角度揭示出经典三回路过载驾驶仪的结构来源。通过改变权值矩阵 Q 和 R 来改变求得增益矩阵，从而改变响应时间。

2 STT 导弹数学模型

在小扰动线性化假设条件下，对弹体动力学模型进行线性化，即李雅普诺夫第一稳定性理论，得到如下数学模型：
在这里插入图片描述
在下文中以俯仰通道为例，应用最优控制理论设计过载驾驶仪，因此仅考虑俯仰通道控制线性方程组。

3 LQR 线性二次型最优控制

3.1 无限时间 LQR 问题

有限时间 LQR 问题只考虑系统在过渡过程中的最优运行，而无限时间 LQR 问题还需考虑系统趋于平衡状态时的渐近性为，因此在控制工程中无限时间 LQR 问题更实用。无限时间 LQR 问题的状态空间模型及目标函数如下：
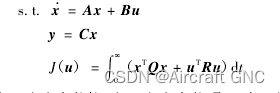
在这里插入图片描述
里卡提方程：

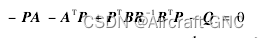
最优控制率：

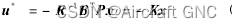
3.2 考虑 Du 项的无限时间 LQR 问题：

在这里插入图片描述

4 基于 LQR 的三回路过载驾驶仪设计

4.1 “惩罚”舵偏角速率的三回路驾驶仪系统状态方程

考虑控制量为舵偏角速率而不是舵偏角，对系统进行增广，增加舵偏角速率的微分方程，此时舵偏角作为一个状态，舵偏角速率为控制量，并将姿态角加速度作为一个输出量，得到新的增广系统状态方程如下：
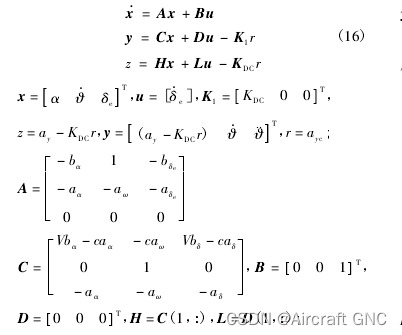
在这里插入图片描述

4.2 性能指标函数及控制率

考虑指令法向过载跟踪问题，对于阶跃指令，跟踪问题可视为定点调节器问题，性能指标函数取法向加速度与加速度指令误差与舵偏角速率加权平方和，如下：
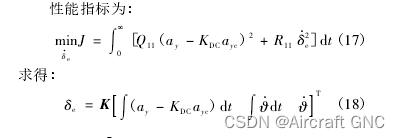
在这里插入图片描述

4.3 Simulink 仿真

根据上述介绍进行仿真验证，取某特征点下的动力学系数如下：

%% 特征点动力学系数
a_wz = 1.5;          
a_alpha = 250;          
a_delta_e = 280;       
b_alpha = 1.6;       
b_delta_e = 0.23;                
V = 914.4;                     
height = 3000;          
c = 0.68;

搭建如下图所示 Simulink 仿真框图：
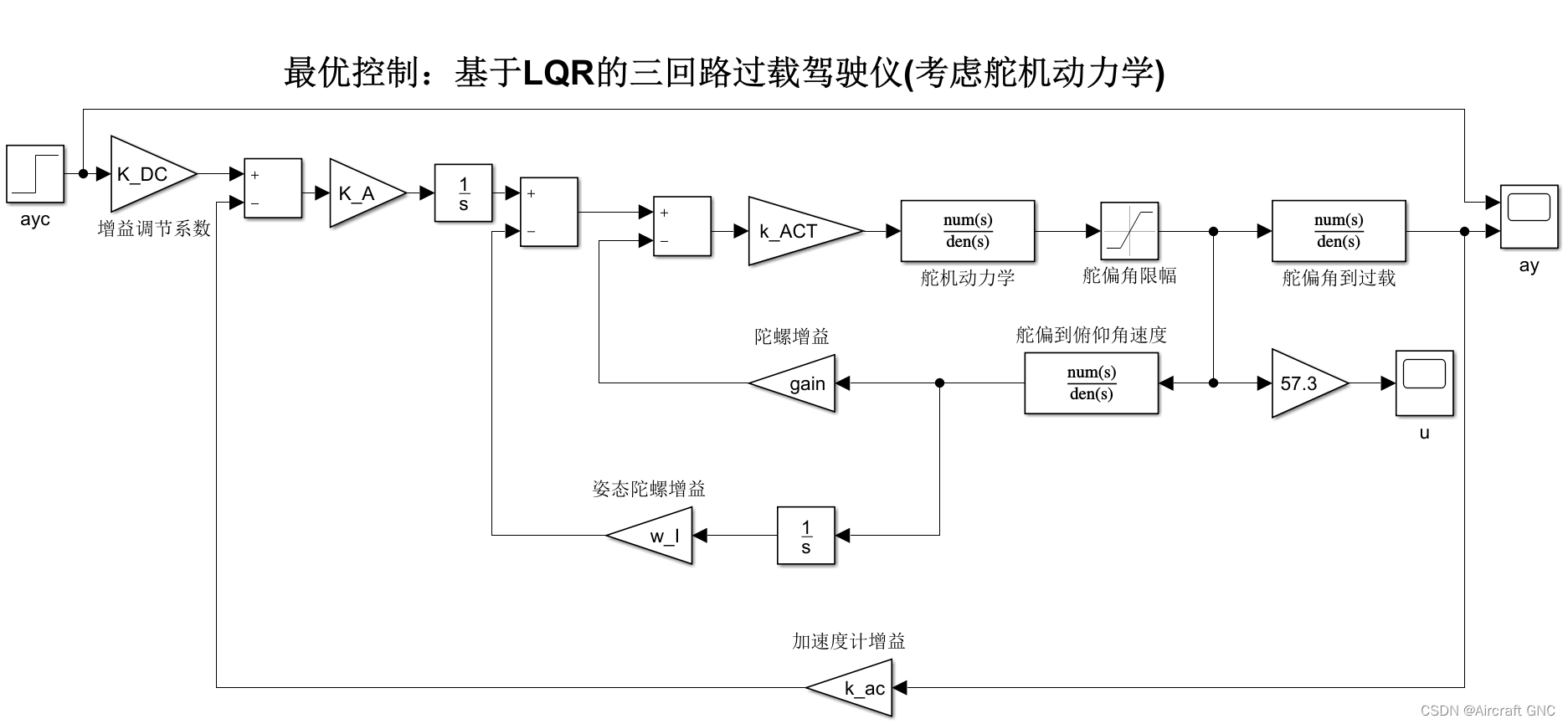
在这里插入图片描述
给定仿真初始条件，得到控制器实际参数如下：K_A = 0.0403; w_I = 3.2225; k_g = 0.1486; K_DC = 1.0874。
开环系统波特图及闭环系统单位阶跃响应：

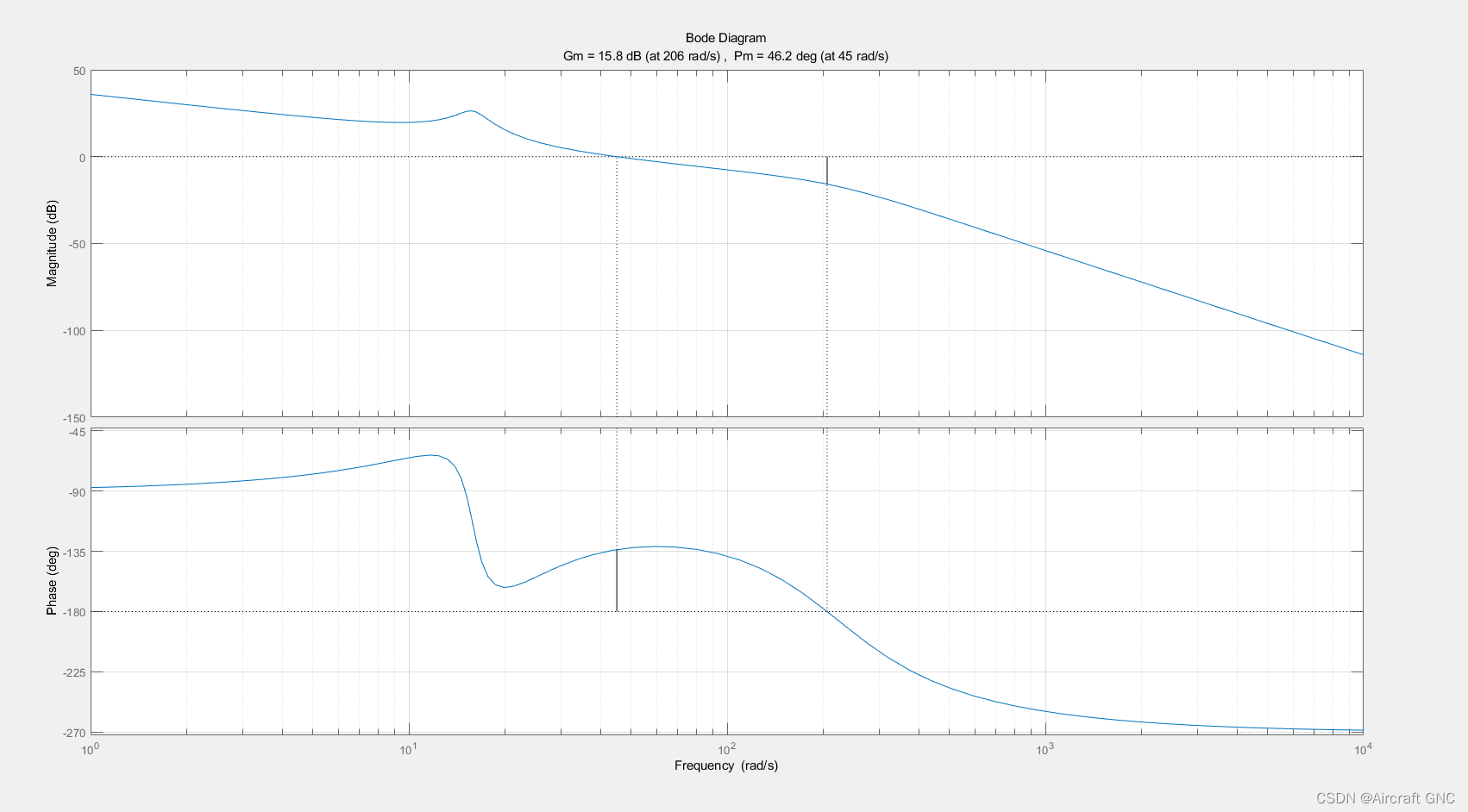
可看出系统有 46.2 deg 的相位裕度以及 15.8 dB 的幅值裕度。

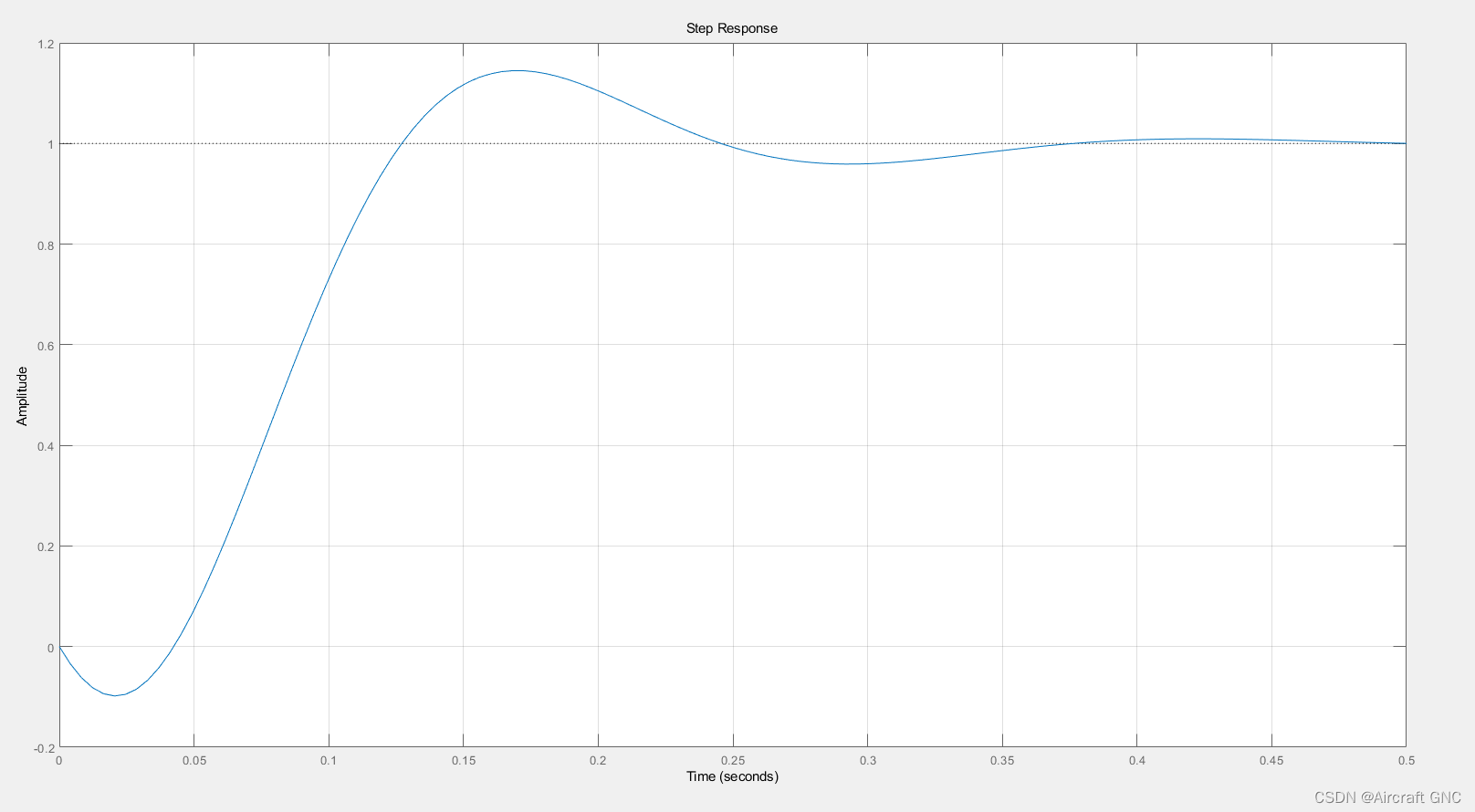
系统在不到 0.4 秒的时候达到了稳定状态，控制器的时域性能指标：峰值时间 0.1684；超调量：14.4793%；上升时间：0.0657；调节时间：0.2218。
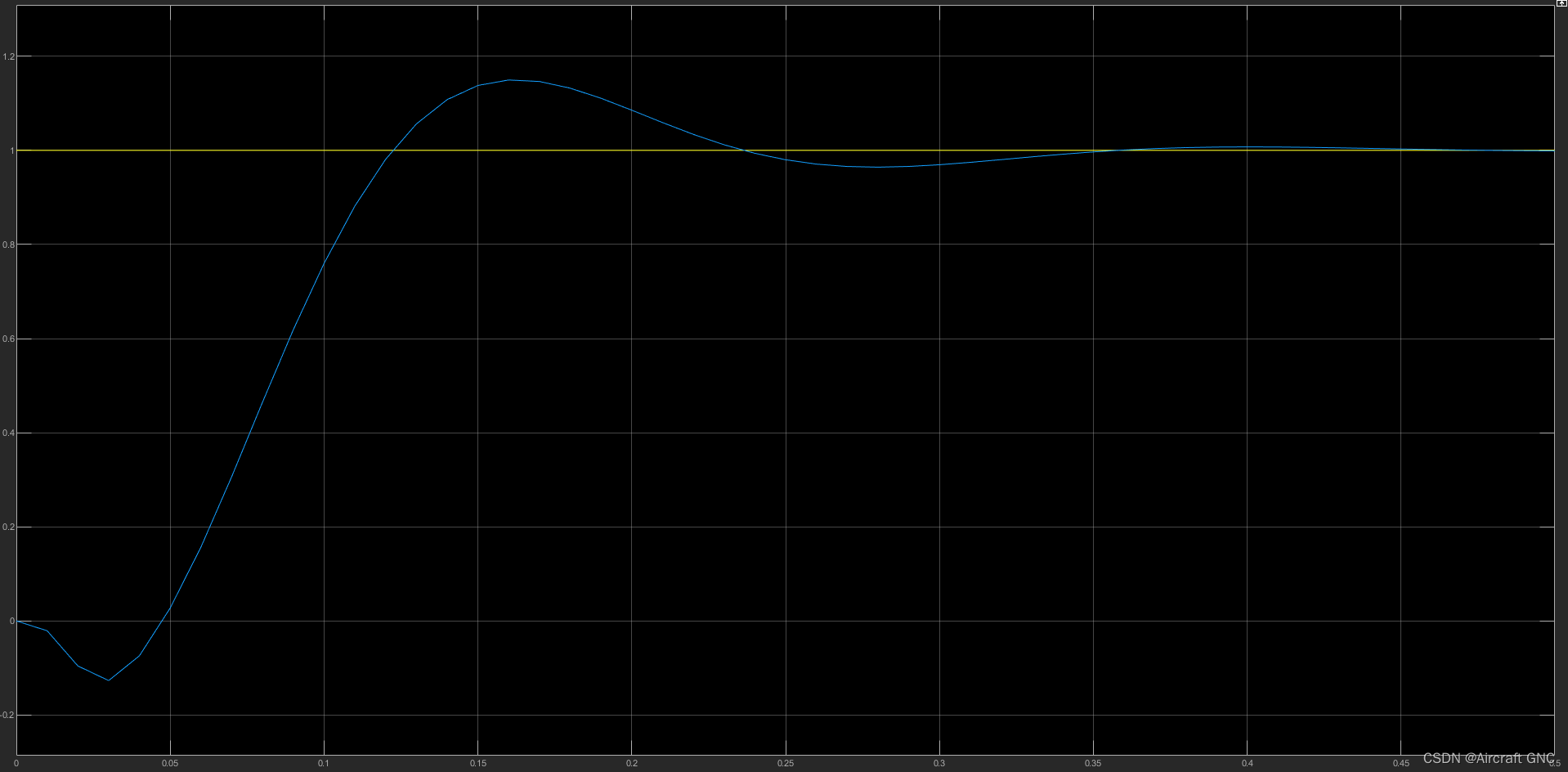
在这里插入图片描述
舵偏角响应曲线：

4.4 讨论

基于 LQR 的两回路过载驾驶仪	基于 LQR 的伪攻角反馈三回路过载驾驶仪
系统状态方程	系统状态方程
性能指标函数	性能指标函数
控制率	控制率
最优控制理论的角度揭示驾驶仪结构	最优控制理论的角度揭示驾驶仪结构

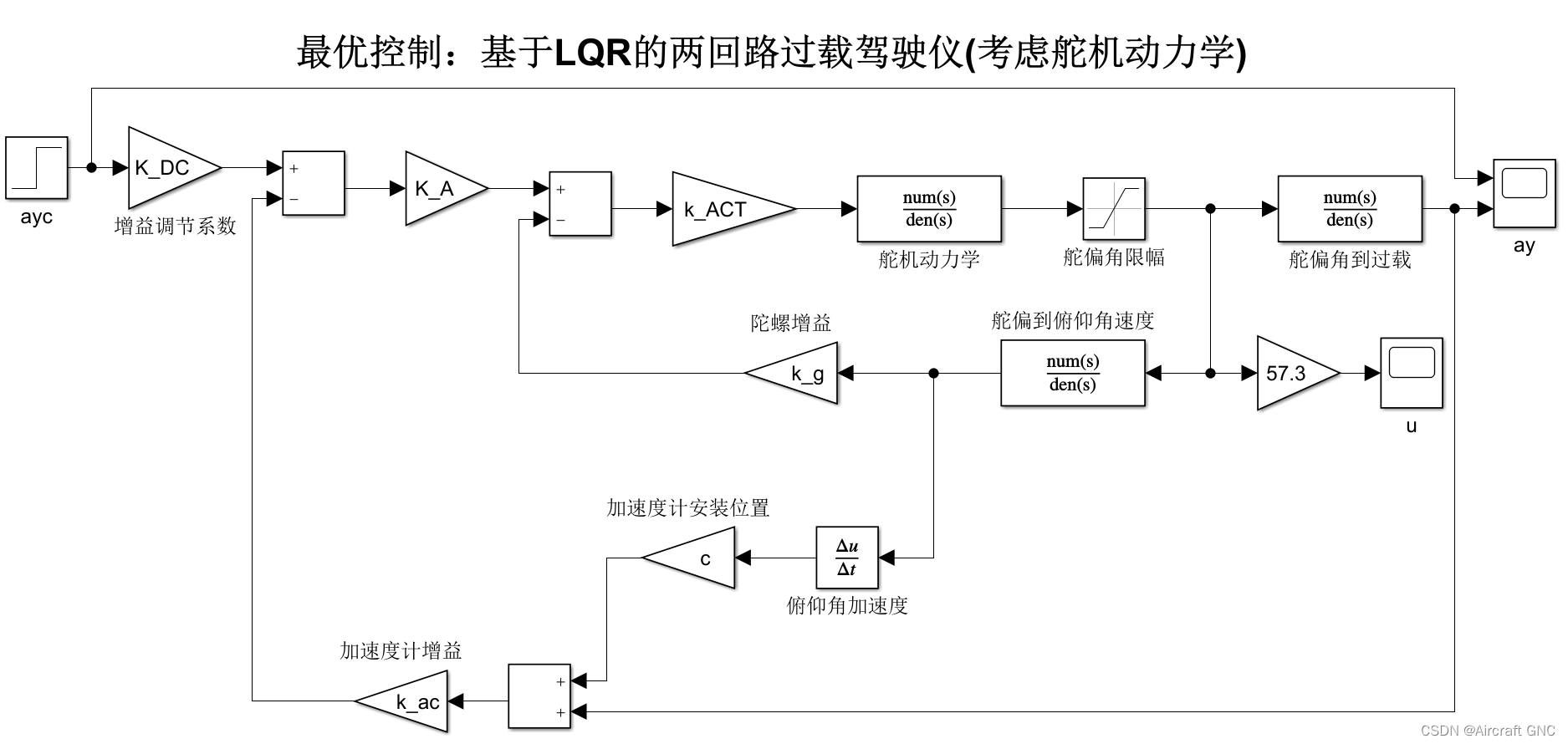
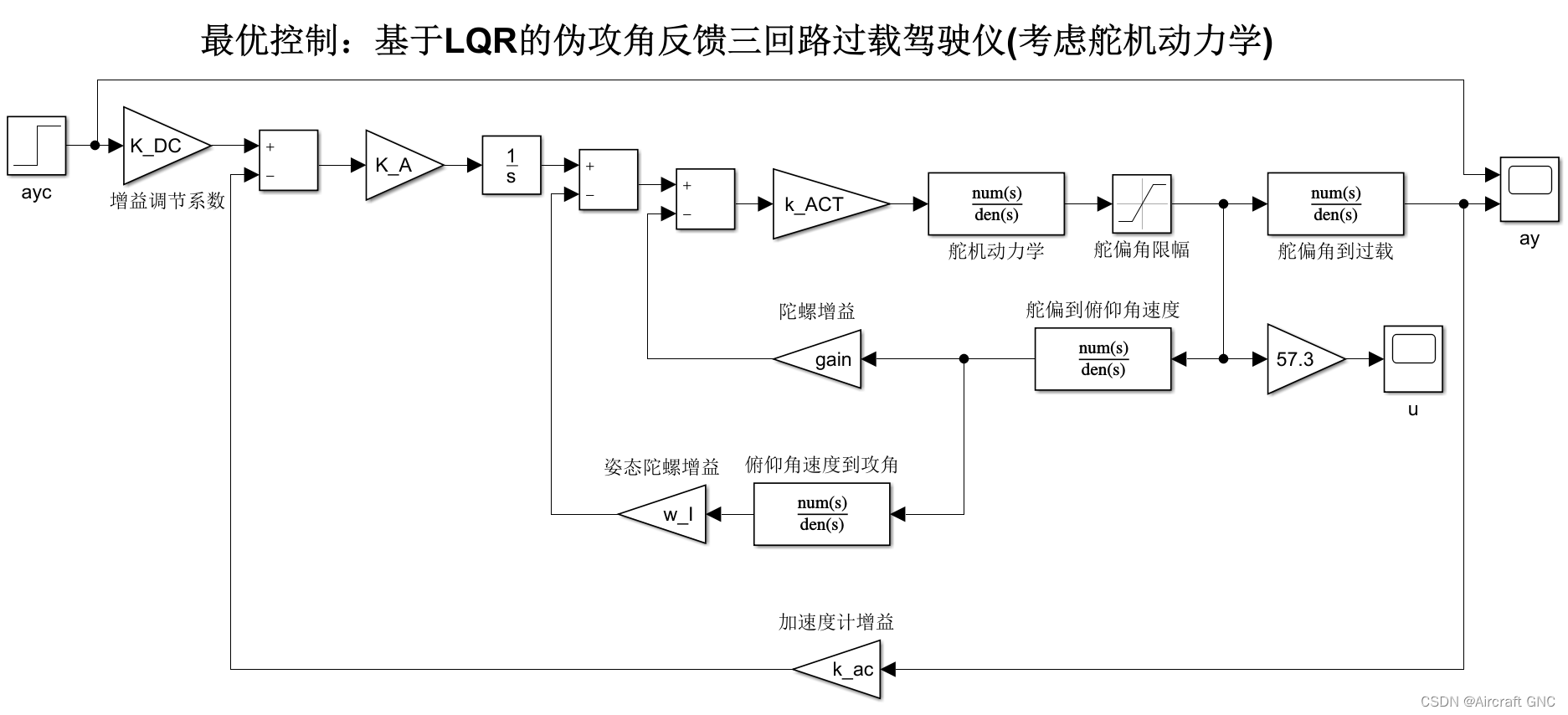
在这里插入图片描述

5 结论

通过前面仿真可看出采用线性二次型最优控制理论设计的 STT 导弹俯仰通道三回路过载驾驶仪具有一定的稳定裕度；且在设计时较经典 PID 控制的三回路过载驾驶仪有一定的灵活性；而且在求出最优控制时，也推导出了对应的自动驾驶仪结构，即可从最优控制理论的角度揭示出经典三回路过载驾驶仪的结构来源。但是 LQR 必须准确测量全部状态变量，在一定程度上限制了其应用，有一种方法是使用最优估计理论，即卡尔曼滤波及其变种来估计系统的状态，感兴趣的朋友可以查阅相关文献进行研究。

6 参考文献

[1] Mracek C P , Ridgely D B . Missile Longitudinal Autopilots: Connections Between Optimal Control and Classical Topologies[C]// AIAA Guidance and Control Conference. 2005.
[2]AIAA. Missile Longitudinal Autopilots: Comparison of Multiple Three Loop Topologies - AIAA Guidance, Navigation, and Control Conference and Exhibit (AIAA)[J]. 2005.
[3]温求遒,夏群力,祁载康.三回路驾驶仪开环穿越频率约束极点配置设计[J].系统工程与电子技术,2009,31(02):420-423.
[4]林德福, 王辉, 王江,等. 战术导弹自动驾驶仪设计与制导律分析[M]. 北京理工大学出版社, 2012.
[5]王辉, 林德福, 祁载康. 导弹伪攻角反馈三回路驾驶仪设计分析[J]. 系统工程与电子技术, 2012, 34(1):129-135.