前言
比赛两个小时,为OI赛制(可以暴力拿部分分的)。一共六道题目
A.整数排序
单点时限:2.0 sec
内存限制:512MB
题面
输入若干个int类型整数,将整数按照位数由大到小排序,如果位数相同,则按照整数本身从小到大排序。例如,
输入:10 -3 1 23 89 100 9 -123
输出:-123 100 10 23 89 -3 1 9
输入的整数个数最多不超过 1 0 6 10^6 106个。
输入格式
在一行中输入若干个整数,整数之间用一个空格分隔。
输出格式
在一行中输出排序好的整数,整数之间用一个空格分隔。
样例
input
10 -3 1 23 89 100 9 -123
ouput
-123 100 10 23 89 -3 1 9
input
1 -2 12
ouput
12 -2 1
思路
? 1.这是一类经典的条件排序问题,它就是排序问题的小变形。由于题目说明了数组长度 n = 1 0 6 n = 10^6 n=106。所以就不要自己写冒泡排序等比较慢的排序了。在C++可直接使用STL中的排序函数函数:sort()。
? 2.就算是你会手写快排,也不建议这么做。因为一方面是比赛的时候浪费时间,另一方面是STL中的sort加了很多优化,它比你手写的快排还会更快。
使用方法
// 1.需要的头文件
#include <algorithm>
// 如果不想记这么多繁杂的头文件,你永远可以相信<万能头文件>,它包罗万象了,至少各种比赛,机试是够用的。
#include <bits/stdc++.h>
// 2.sort的使用方法
sort (起始地址,结束地址的下一位,自定义排序函数的函数名)
// 起始/结束地址:传入对应的指针,一定要注意是结束的地址的下一位!
// 自定义排序函数:告诉sort函数将如何比较两个数,谁放在前面,谁放在后面。不传参时默认是升序排序。
// 3.具体案例1:给定一个整数数组a,我们希望对其下标为[l,r]的区域<升序>排序
sort(a + l , a + r + 1)
回到这道题,它的关键其实就是构造自定义排序函数。我们来展开讲一讲这一点。
//具体案例2:给定一个整数数组a,我们希望对其下标为[l,r]的区域<降序>排序
//这时我们可以自己构造一个自定义排序的函数cmp(函数名随意命名),然后将函数名填入第三个参数(这个在语法上叫做函数传参,本质是传递函数指针)
sort(a + l , a + r + 1 , cmp);
// 返回值为bool型,传入两个参数a , b
// 这个函数的作用是告诉sort函数将如何比较两个数。当返回true的时候将a放在b之前,返回false的时候将b放在a之前
bool cmp (const int& a , const int& b){
//if (a > b) return true;
//else return false;
//利用语法特性,直接返回逻辑表达式
return a > b;
}
// 更多解释:1.利用引用变量是为了加快速度,减少拷贝时间。2.使用const修饰是为了防止我们误改内容。
//所以你不加这两个,直接写int a , int b 也不会有问题,只是不规范罢了。
所以这题的关键就是构造自定义排序函数cmp。代码如下:
#include <bits/stdc++.h>
using namespace std;
struct Val{
int dig; // 数位长度
int val; // 数字
};
Val a[1000006];
// 获得数位长度
int getDig (int val){
val = abs(val);
int ans = 0;
while (val){
ans ++;
val /= 10;
}
return ans;
}
int cmp (const Val & a , const Val& b){
if (a.dig != b.dig)
return a.dig > b.dig;
return a.val < b.val;
}
int main() {
int x , n = 0;
while (cin >> x) {
a[++n].val = x;
a[n].dig = getDig(a[n].val);
}
sort(a + 1 , a + n + 1 , cmp);
for (int i = 1 ; i <= n ; i++){
cout << a[i].val;
if (i == n) cout << endl;
else cout << " ";
}
return 0;
}
总结
评价
这是机试第一题,难度比较小。如果平时有在刷题应该是能秒掉的。
关键
条件排序
B.位运算
单点时限:2.0 sec
内存限制:512MB
题面
给定一个int型整数 x x x,将 x x x的二进制表示中第i位和第j位的值互换。 0 ≤ i , j ≤ 31 0 \leq i,j \leq 31 0≤i,j≤31
注意: x x x的二进制表示的最右边为第0位。
输入格式
在一行中输入三个整数, x , i , j x,i,j x,i,j, 整数之间用一个空格分隔。
输出格式
在一行中输出互换后的结果
样例
input
38 2 4
ouput
50
input
1 0 2
ouput
4
思路
思路很自然:获取 x x x二进制表示中的第 i i i位与第 j j j位。之后将他们互换即可。
问题在于:实现方法很多
1.将其转化成二进制数组a,然后模拟swap(a[i] , a[j])后再转换回十进制数
2.利用位运算的技巧去做
第一步:获得二进制第 i , j i,j i,j位置上的值。
具体的:将数 x x x右移 i / j i/j i/j位然后将其与上1。
a = ( x > > i ) & 1 a=(x >> i)\&1 a=(x>>i)&1
b = ( x > > j ) & 1 b=(x >> j)\&1 b=(x>>j)&1
第二步:互换,具体的, x i = b x_i=b xi?=b, x j = a x_j=a xj?=a
只有当 a ≠ b a \neq b a?=b 时才需要交换。而交换的结果就是取反即可。而取反我们可以利用<异或1>来完成。
if (a != b){
x ^= (1 << i);
x ^= (1 << j);
}
实现
#include <bits/stdc++.h>
using namespace std;
int main() {
int x , i , j;
cin >> x >> i >> j;
int a = (x >> i) & 1;
int b = (x >> j) & 1;
// 更简洁的表示方法,甚至可以省去判断
x ^= ((a ^ b) << i);
x ^= ((a ^ b) << j);
cout << x << endl;
return 0;
}
总结
??评价:位运算的简单考察,应该要拿满分。
C.差分计数
单点时限:0.5 sec
内存限制:512MB
题面
给定 n n n个整数 a 1 , . . . , a n a_1,...,a_n a1?,...,an?和一个整数 x x x。求有多少有序对 ( i , j (i,j (i,j)满足 a i ? a j = x a_i-a_j= x ai??aj?=x。
输入格式
第一行两个整数 n ( 1 ≤ n ≤ 2 × 1 0 6 ) , x ( ? 2 × 1 0 6 ≤ x ≤ 2 × 1 0 6 ) n(1 \leq n \leq 2 \times 10^6),x(-2 \times 10^6 \leq x \leq 2 \times 10^6) n(1≤n≤2×106),x(?2×106≤x≤2×106),分别代表整数的个数和题目中的 x x x。
第二行 n n n个用空格隔开的整数,第 i i i个代表 ? 2 × 1 0 6 ≤ a i ≤ 2 × 1 0 6 -2 \times 10^6 \leq a_i \leq 2 \times 10^6 ?2×106≤ai?≤2×106
输出格式
一行一个整数,代表满足 a i ? a j = x a_i-a_j=x ai??aj?=x的有序对 ( i , j ) (i,j) (i,j)个数。
样例
input
5 1
1 1 5 4 2
ouput
3
笔者说明
( 1 ( 1 ) , 2 ( 5 ) ) , ( 1 ( 2 ) , 2 ( 5 ) ) , ( 5 ( 3 ) , 4 ( 4 ) ) (1(1),2(5)),(1(2),2(5)),(5(3),4(4)) (1(1),2(5)),(1(2),2(5)),(5(3),4(4)) 这三个有序对。
思路
1.自然暴力解法
??双重循环枚举 i , j i,j i,j 来计数即可,复杂度是 O ( n 2 ) O(n^2) O(n2)。但是无法拿到满分。 服务器一般一秒跑 1 e 8 1e8 1e8 次。把 n n n 带进去看看 ( 2 ? 1 0 6 ) 2 = 4 ? 1 0 12 远 大 于 1 e 8 (2 * 10^6)^2=4 * 10^{12} 远大于 1e8 (2?106)2=4?1012远大于1e8
2.前缀暴力法(正确算法的暴力版本)
??考虑枚举每一个
a
j
a_j
aj?(有序对的后面那个数), 观察题目所给等式
a
i
?
a
j
=
x
a_i-a_j=x
ai??aj?=x
??这时
a
j
a_j
aj?已经被固定,那它和
x
x
x一样是一个常数,将常数放在一边,可以得到
a
i
=
x
+
a
j
a_i=x+a_j
ai?=x+aj?
??这时也就是找
i
∈
[
1
,
j
?
1
]
i \in [1,j-1]
i∈[1,j?1] 内的数中有多少个数为
x
+
a
j
x+a_j
x+aj?。
??不难发现,不管
j
j
j取什么值,这样的区域总是一个前缀,我们可以将前缀:
i
∈
[
1
,
j
?
1
]
i \in [1,j-1]
i∈[1,j?1]的所有
a
i
a_i
ai? 放入到一个哈希表
H
H
H 当中,然后直接查询
H
[
x
+
a
j
]
H[x+a_j]
H[x+aj?] 即可。整个过程如下所示,还是以题目样例为例子分析:
1
?
1
?
5
?
4
?
2
1\ 1\ 5\ 4\ 2
1?1?5?4?2
| 位置 j j j | a j a_j aj? | 前缀 | x + a j x+a_j x+aj? | 答案贡献 |
|---|---|---|---|---|
| 1 | 1 1 1 | ? \empty ? | 2 2 2 | 0 0 0 |
| 2 | 1 1 1 | { 1 } \{1\} {1} | 2 2 2 | 0 0 0 |
| 3 | 5 5 5 | { 1 , 1 } \{1,1\} {1,1} | 6 6 6 | 0 0 0 |
| 4 | 4 4 4 | { 1 , 1 , 5 } \{1,1,5\} {1,1,5} | 5 5 5 | 1 1 1 |
| 5 | 2 2 2 | { 1 , 1 , 5 , 4 } \{1,1,5,4\} {1,1,5,4} | 2 2 2 | 2 2 2 |
| 总答案 | 1 + 2 = 3 1+2=3 1+2=3 |
3.维护前缀法
??其实咱们将表格画出来后就能够马上看到规律,意识到一个问题:前缀的变化是连续的,也就是说:第 k k k个前缀与第 k ? 1 k-1 k?1个前缀相比只是多了一个 a k a_k ak?.所以咱们完全就没必要每次都把哈希表清空然后重新构造前缀的哈希表,而只是需要每次往哈希表里插入新的值即可。那么做法其实就很显然了~
??显然这个问题的复杂度就是 O ( n ) O(n) O(n)的
实现
? 注意,在实现的过程中还是需要注意很多细节问题。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 5;
int a[maxn];
int b[maxn * 2]; // 注意:b的下标填的是值域范围,不是数组长度,所以需要开两倍
// 下标变换
int idTrans (int x){
// 这时下标从[-2e6,2e6]映射到[0,4e6]
return x + 2e6;
}
int main() {
int n , x;
cin >> n >> x;
for (int i = 1 ; i <= n ; i++)
cin >> a[i];
// 答案可能很大:考虑ai全等且x=0,那么任意两个i,j都是一个答案。那么答案会是n^2阶的。
// 尝试将其带进去会发现它爆int了,所以只能用long long 存储
long long ans = 0;
// hash表可以用STL中的unordered_map,但是我们发现下标其实没那么大
// 所以为了更快的运行速度我们可以开一个桶数组b。
// 但是值域涉及到负数,所以需要做一个下标的映射.
for (int j = 2 ; j <= n ; j++){
ans += b[idTrans(a[j] + x)];
b[idTrans(a[j])]++;
}
cout << ans << endl;
return 0;
}
总结
评价
??本题正式涉及到算法思想,鉴定为竞赛入门难度。
关键
??这道题的优化关键在于前缀的连续变化性。可以复用哈希表
拓展
??1.将题目中的 a i ? a j = x a_i-a_j= x ai??aj?=x 改成 a i ? a j = i ? j a_i-a_j= i-j ai??aj?=i?j
??2.序列中有多少个子段的和恰好为
x
x
x,即求有多少有序对(
i
,
j
i,j
i,j)满足
∑
k
=
i
j
a
k
=
x
\sum_{k=i}^{j}a_k=x
k=i∑j?ak?=x
??3.序列中有多少个子段的和为
x
x
x的倍数,即求有多少有序对
(
i
,
j
(i,j
(i,j)满足
∑
k
=
i
j
a
k
≡
0
?
(
m
o
d
?
x
)
\sum_{k=i}^{j} a_k \equiv 0 \ (mod\ x)
k=i∑j?ak?≡0?(mod?x)
??4.序列中有多少个子段的平均值恰好为
x
x
x,即求有多少有序对
(
i
,
j
(i,j
(i,j)满足
∑
k
=
i
j
a
k
j
?
i
+
1
=
x
\frac{\sum_{k=i}^{j} a_k}{j-i+1}=x
j?i+1∑k=ij?ak??=x
D.罗马数字
单点时限:2 sec
内存限制:512MB
题面
罗马数字是古罗马使用的记数系统,现今仍很常见。
罗马数字有七个基本符号: I,V,X,L,C,D,M。
| 罗马数字 | I | V | X | L | C | D | M |
|---|---|---|---|---|---|---|---|
| 对应的阿拉伯数字 | 1 1 1 | 5 5 5 | 10 10 10 | 50 50 50 | 100 100 100 | 500 500 500 | 1000 1000 1000 |
需要注意的是罗马数字与十进位数字的意义不同,它没有表示零的数字,与进位制无关。按照下述的规则可以表示任意正整
数。
“标准”形式
重复次数:一个罗马数字重复几次,就表示这个数的几倍。
左加右减:
- 1.在较大的罗马数字的右边记上较小的罗马数字,表示大数字加小数字。
- 2.在较大的罗马数字的左边记上较小的罗马数字,表示大数字减小数字。
- 3.左减的数字有限制,仅限于I,X,C.例如 45 45 45表示XLV,而不是VL
- 4.左减时不可跨越一个位值。例如, 99 99 99是XCIX$ ([100- 10]+ [10- 1])$,而不是IC ( [ 100 ? 1 ] ) ([100 - 1]) ([100?1])。等同于阿拉伯数字每位数字分别表示。
- 5.左减数字必须为一位,比如 8 8 8是VIII,而不用IIX
- 6.罗马数字V,L,D中的任何一个放在较大的罗马数字右边只能使用一个。
- 7.右加连续相同数字不超过三位,比如 14 14 14是XIV,而不是XIIII
现在给出一个阿拉伯数字表示的十进制正整数,输出其对应的罗马数字。
输入格式
一行十进制整数
输出格式
一行字符串,表示对应的罗马数字
样例
input
3
output
III
思路
??这题最主要的难点就是规则繁杂。最快的理解规则方式是,先把 1 ? 10 1-10 1?10 都表示出来!
| 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 罗马数字 | I | II | III | IV | V | VI | VII | VIII | IX | X |
根据条件7, 1 , 2 , 3 1,2,3 1,2,3 一定是 I,II,III
对于4,根据条件7,不能是IIII,所以根据条件2得到:IV. 对于9是同理的
??我们发现这样的规律很容易推广到10,20,…,100 与 100 , 200 , 300 , … , 1000
| 十进制 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| 罗马数字 | X | XX | XXX | XL | L | LX | LXX | LXXX | XC | C |
| 十进制 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|
| 罗马数字 | C | CC | CCC | CD | D | DC | DCC | DCCC | CM | M |
??有上面三张表,我们就可以表示出 [ 1 , 1000 ] [1,1000] [1,1000] 内的任何一个数。只需要拆分十进制位即可。
??例如: 338 = 300 + 30 + 8 338=300+30+8 338=300+30+8。所以是 C C C X X X V I I I CCCXXXVIII CCCXXXVIII
实现
1.存表
2.将读入的数十进制拆分
3.查表输出
代码:略
总结
评价
??一道简单的模拟题。
E.乘法
单点时限:1.0 sec
内存限制:256MB
题面
给出一个长度为 n n n的数列和一一个长度为 m m m的数列,可以构造得到一个 n × m n\times m n×m的矩阵C,其中 C i , j = A i × B j C_{i,j}= A_i \times B_j Ci,j?=Ai?×Bj?。
给出整数 K K K,你需要求出 C C C中的第 k k k大的数的值。
输入格式
第一行输入三个整数 n , m , K n, m,K n,m,K( 1 ≤ n , m ≤ 1 0 5 , 1 ≤ K ≤ n × m 1 \leq n,m≤10^5,1\leq K \leq n \times m 1≤n,m≤105,1≤K≤n×m)。
第二行输入 n n n个空格隔开的整数 A 1 , A 2 , . . . , A n ( ? 1 0 6 ≤ A i ≤ 1 0 6 ) A_1, A_2,...,A_n(-10^6≤A_i≤10^6) A1?,A2?,...,An?(?106≤Ai?≤106)
第三行输入 m m m个空格隔开的整数 B 1 , B 2 , . . . , B m ( ? 1 0 6 ≤ B i ≤ 1 0 6 ) B_1, B_2,...,B_ m(-10^6≤B_i≤10^6) B1?,B2?,...,Bm?(?106≤Bi?≤106)
输出格式
输出一行一 个整数,表示矩阵中的第 K K K大的数的值。
样例
input
3 3 3
2 3 4
4 5 6
output
18
思路
1.暴力
?? 两重循环得到 C C C中的所有值,之后降序排序访问第 K K K个数即可。 O ( n 2 ) O(n^2) O(n2)但无法通过全部数据。
2.拓展法
?? 因为要知道第 k k k大的数。所以自然是希望先将 A , B A,B A,B数组降序排序。如此我们知道 A 1 × B 1 A_1 \times B_1 A1?×B1? 一定是最大值。问题在于次大值是谁?
A 1 × B 2 ? 与 ? A 2 × B 1 A_1 \times B_2\ 与 \ A_2 \times B_1 A1?×B2??与?A2?×B1? 都有可能,如下
A = [ 6 ? 5 ] A = [6\ 5] A=[6?5]
B = [ 6 ? 1 ] B = [6\ 1] B=[6?1]
或者
A = [ 6 ? 1 ] A = [6\ 1] A=[6?1]
B = [ 6 ? 5 ] B = [6\ 5] B=[6?5]
??而且我们容易知道除了这两种情况以外没有其他可能的位置能形成次大值了。所以我们把上面这个考虑两种情况的操作称之为拓展
以下过程均视为 A , B A,B A,B数组已被降序排序。
??我相信刷过这类题的人知道过程是用大根堆维护,每次删最大数,然后拿他拓展再塞回大根堆。这样进行 k ? 1 k-1 k?1轮,堆顶就是第 k k k大的数。(力扣上的丑数II那道题也是这样做的)
??这样的算法容易感觉出来是对的,但笔者尝试说明一下算法的正确性
"大白话"证明
??不妨看一个更显然的结论:在已知前 k ? 1 k-1 k?1大的乘积并且他们的方案的情况下(即知道 k ? 1 k-1 k?1个三元组 < A i × B j , i , j > <A_i \times B_j , i,j> <Ai?×Bj?,i,j>)。那么第 k k k大的乘积一定出自这 k ? 1 k-1 k?1个方案中某一个的拓展的结果。
??这个结论很显然,因为假设第 k k k大的数为 A i × B j A_i \times B_j Ai?×Bj? ,那么它可以看作是由$A_{i-1} \times B_j $ 拓展而来。而显然 A i ? 1 × B j > A i × B j A_{i-1} \times B_j > A_i \times B_j Ai?1?×Bj?>Ai?×Bj?,所以 A i ? 1 × B j A_{i-1} \times B_j Ai?1?×Bj? 一定是前 k ? 1 k-1 k?1里的某一个。
1.这里可能有人会发现: i = 1 i=1 i=1这个结论还对么?
??还是对的,因为也可以看作是 A i × B j ? 1 A_{i}\times B_{j-1} Ai?×Bj?1?拓展 。
2.进一步的:要是这个时候 j = 1 j=1 j=1 呢??
??这种情况就是 A 1 × B 1 A_1 \times B_1 A1?×B1? , 这种情况是特例,它一定是第 1 1 1大~
??所以根据这个结论我们容易设计一个暴力的算法
??用一个集合
S
S
S维护前
k
?
1
k-1
k?1大的方案。然后通过拓展操作得到
2
×
(
k
?
1
)
2 \times (k-1)
2×(k?1) 个可能的结果,从中选一个集合中没出现过的最大值,插入到集合
S
S
S中。如此往复该过程即可,如下图所示
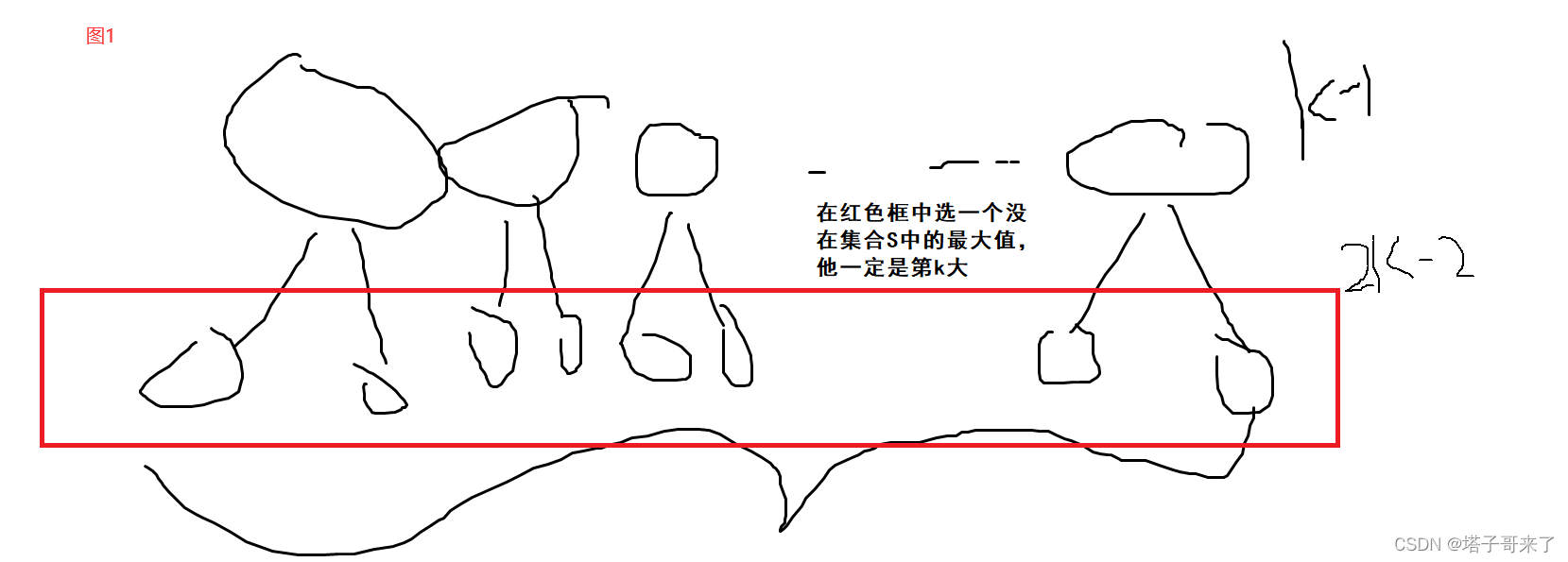
??但是这样的复杂度是 O ( k 2 ) O(k^2) O(k2) 的。不过由于集合 S S S中的每个元素只有可能被拓展成两个元素,它和k是多大无关。
??比如:第1大的数 < A 1 × B 1 , 1 , 1 > <A_1 \times B_1,1,1> <A1?×B1?,1,1> 它总是会被拓展成 < A 1 × B 2 , 1 , 2 > 与 < A 2 × B 1 , 2 , 1 > <A_1 \times B_2,1,2>与<A_2 \times B_1,2,1> <A1?×B2?,1,2>与<A2?×B1?,2,1>,不管是在第几轮
??所以将集合
S
S
S中的
<
A
1
×
B
1
,
1
,
1
>
<A_1 \times B_1,1,1>
<A1?×B1?,1,1> 替换成
<
A
1
×
B
2
,
1
,
2
>
与
<
A
2
×
B
1
,
2
,
1
>
<A_1 \times B_2,1,2>与<A_2 \times B_1,2,1>
<A1?×B2?,1,2>与<A2?×B1?,2,1> 是一步等价操作,不改变算法正确性。而且对于第
i
,
i
∈
[
1
,
k
]
i,i \in [1,k]
i,i∈[1,k]大的元素这个性质都成立。所以我们可以给所有元素进行拓展替换。所以不难发现,我们完全可以不去维护集合
S
S
S,而是直接维护待拓展集合
T
T
T,如下图所示
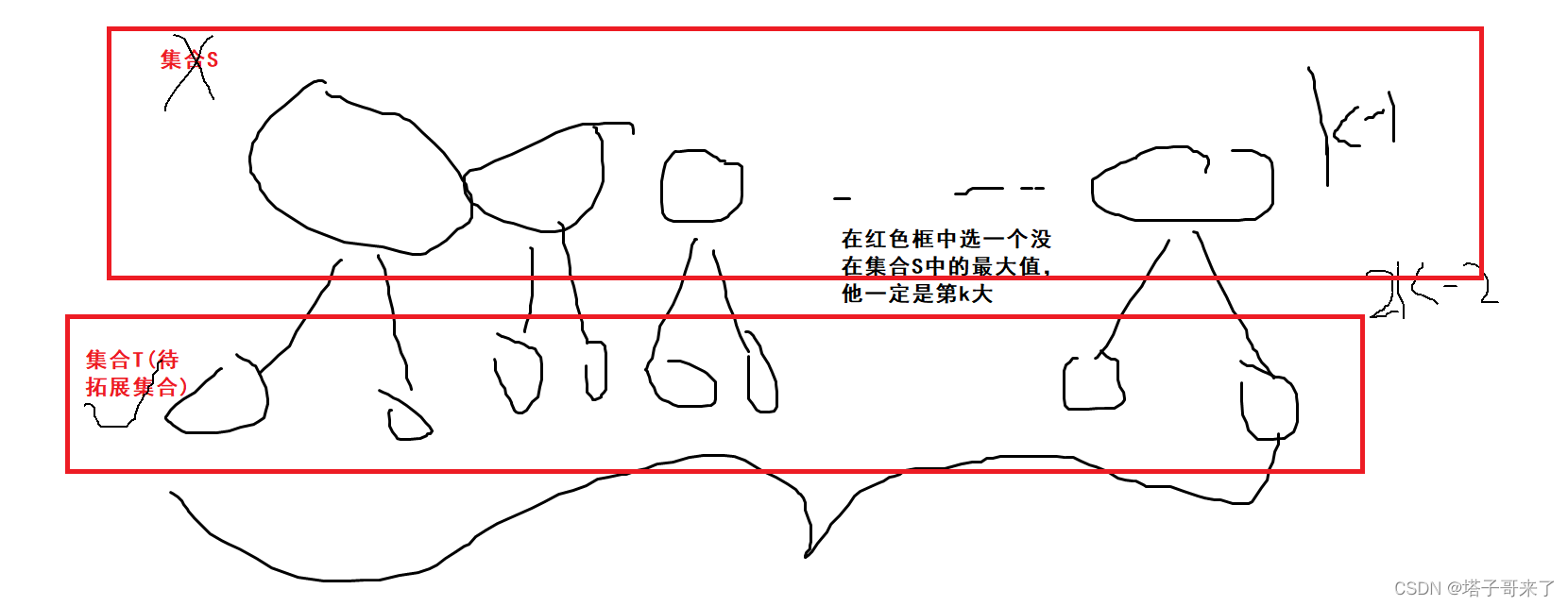
??至此,我们就是反复的从集合
T
T
T中拿出最大值,删掉它,然后对它进行拓展。
k
?
1
k-1
k?1轮之后集合的最大值就是第
k
k
k大的结果。
??这恰恰对应着最初的算法。我们大概可以信任这个算法是对的了。因为我们上述优化的每一步都是等价操作。所以只要暴力算法是对的,最终的优化算法就是对的。
这里可能有部分读者觉得证明就要严谨,上述不够符号化,太大白话了。但是我认为证明一旦过于严谨,那对于小白来讲难度就成倍增加。所以还是直白的解释好些。
实现
略
总结
F.Minimum_Sum
单点时限:2.0 sec
内存限制:256MB
题面
你有一个序列
a
1
,
a
2
,
.
.
.
,
a
n
a_1,a_2,...,a_n
a1?,a2?,...,an?,然后给你一些区间
[
l
,
r
]
[l,r]
[l,r].对于每一个区间,你需要找到下式的最小值,对于所有可能的
x
x
x
∑
i
=
l
r
∣
x
?
a
i
∣
\sum_{i=l}^{r}|x-a_i|
i=l∑r?∣x?ai?∣
输入格式
第一行一个整数 N N N 代表序列长度。
接下来一行有 N N N个正整数 a i ( 1 ≤ a i ≤ 1 0 9 ) a_i(1 \leq a_i \leq 10^9) ai?(1≤ai?≤109),用空格隔开。
接下来一行一个整数 Q ( 1 ≤ Q ≤ 1 0 5 ) Q(1 \leq Q \leq 10^5) Q(1≤Q≤105),代表询问的区间次数。
接下来 Q Q Q行,每行一个区间 l , r ( 1 ≤ l ≤ r ≤ N ) l,r(1 \leq l \leq r \leq N) l,r(1≤l≤r≤N)
输出格式
输出 Q Q Q行。每行代表对应的区间的结果。
思路
最小化曼哈顿距离
??1.对于给定的区间
[
l
,
r
]
[l,r]
[l,r]。我们如何确定这个
x
x
x呢?即
a
r
g
m
i
n
x
?
∑
i
=
l
r
∣
x
?
a
i
∣
\Large \underset{x}{argmin}\ \sum_{i=l}^{r}|x-a_i|
xargmin??i=l∑r?∣x?ai?∣
这其实本质就是最小化曼哈顿距离。我们先考虑对于整个序列的情况:
它的结论是: 对序列 a a a排序后
1.当 n n n是奇数时, x ? = a n / 2 + 1 x^*=a_{n / 2 +1} x?=an/2+1? , 也就是序列的中位数。
2.当 n n n是偶数的时候 x ? ∈ [ a n / 2 , a n / 2 + 1 ] x^* \in[a_{n / 2},a_{n / 2 + 1}] x?∈[an/2?,an/2+1?]
??直观的理解:当
x
x
x 在中位数的位置时,我们无论是往左移动还是往右移动,都会有超过
n
/
2
n / 2
n/2 个点在远离他。那么结果一定会变大。如下图所示
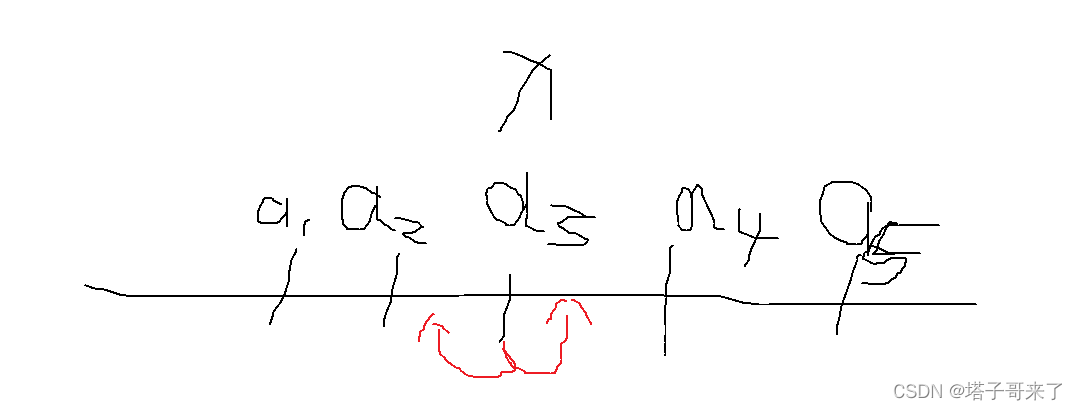
如果往左移动一个单位,会有3个点在远离,2个点在靠近
同样的,如果往右移动一个单位,会有3个点在远离,2个点在靠近.所以中间的位置最小。
当然严格的数学证明在此:点我,这里笔者不展开了
暴力解法
??所以我们有了一个暴力的做法:对于询问的区间
[
l
,
r
]
[l,r]
[l,r],拷贝一份出来对其排序,然后根据结论得到中位数。再计算值后输出。但是这个做法无法拿满分。这题本质变为1.求解区间中位数 2.求解区间关于某一值域的和即
求
序
列
上
区
间
[
l
,
r
]
中
值
域
为
[
x
,
y
]
的
数
的
和
求序列上区间[l,r]中值域为[x,y]的数的和
求序列上区间[l,r]中值域为[x,y]的数的和
高级数据结构优化
??至此,本题变成一道可持久化值域线段树(主席树)的模板题。在结点上维护叶节点个数以及叶节点的权值和即可。
当然这是笔者口胡的做法,没有实际去实现。大家有更好的做法欢迎在评论区留言!
总评
??总体难度不大,都是非常常见的机试题。当时考场上分数集中在 [ 200 , 300 ] [200,300] [200,300]之间。