void shade(p, wo)
{
    //随机生成N个方向的wi并以pdf(wi)分布
    L0 = 0.0;
    //对每条wi
    For each wi
    {
        //向wi方向追踪一条射线ray r(p,wi)
        Trace a ray r(p,wi)
        //如果射线击中光源（相交）
        If ray r hit the light
            //写出求和式
            L0 += (1 / N) * L_i * f_r * cosine / pdf(wi)
    }
    return L0;
}

直接光照考虑完了之后，接下来要看间接光照，关于直接光照和间接光照内容可以参考：GAMES101作业5-从头到尾理解代码&Whitted光线追踪_flashinggg的博客-CSDN博客

间接光照 indirect illumination

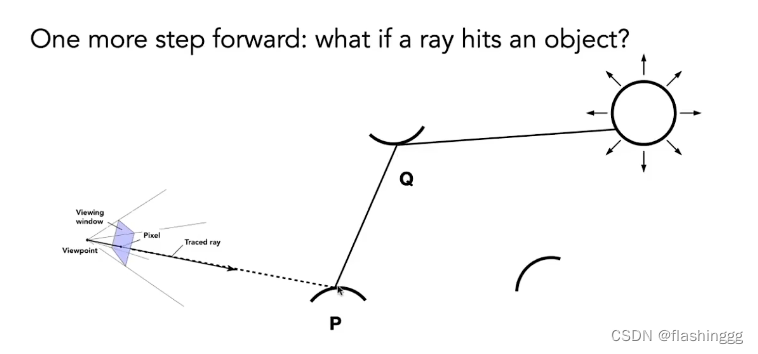
如图所示，开始求光线击中物体的情况。从上图看，可以看作从P点观察Q点，把Q点当作直接光照，这就跟之前的联系起来了，就可以在直接光照伪代码的基础上加上：

//射线击中物体上的p点（射线r与q相交）
Else if ray r hit an object at q
L0 += (1 / N) * shade(q,-wi) * f_r * cosine / pdf(wi)

合成全局光照

加上后，就得到一个递归的、支持全局光照的伪代码：

void shade(p, wo)
{
    //随机生成N个方向的wi并以pdf(wi)分布
    L0 = 0.0;
    //对每条wi
    For each wi
    {
        //向wi方向追踪一条射线ray r(p,wi)
        Trace a ray r(p,wi)
        //如果射线击中光源（相交）
        If ray r hit the light
        //写出求和式
        L0 += (1 / N) * L_i * f_r * cosine / pdf(wi)
        //射线击中物体上的p点（射线r与q相交）
        Else if ray r hit an object at q
        L0 += (1 / N) * shade(q,-wi) * f_r * cosine / pdf(wi)
    }
    return L0;
}

但我们的问题还未完全解决！

解决一些存在的问题

问题1：光线爆炸

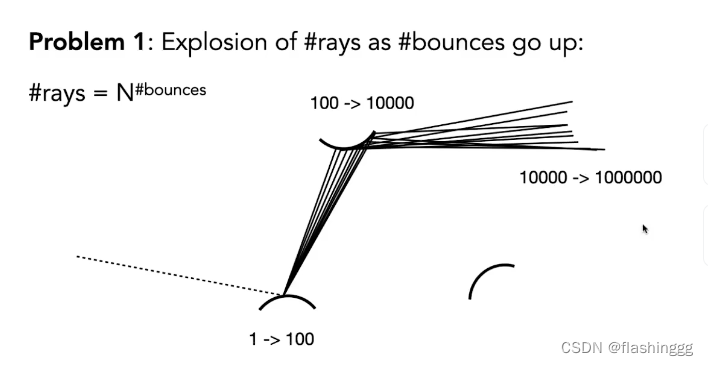
由于加入了递归，导致发出的光线数量呈指数增长！计算量将爆炸！很明显，只有N==1的时候，才能解决这个问题，伪代码将修改成这样：

void shade(p, wo)
{
    //随机选取1个方向的wi并以pdf(wi)分布
    L0 = 0.0;
    //向该方向追踪一条射线ray r(p,wi)
    Trace a ray r(p,wi)
    //如果射线击中光源（相交）
    If ray r hit the light
    //写出求和式
    Return L_i * f_r * cosine / pdf(wi)
    //射线击中物体上的p点（射线r与q相交）
    Else if ray r hit an object at q
    Return shade(q,-wi) * f_r * cosine / pdf(wi)
}

由此，N==1，就是我们做的Path Tracing路径追踪。

上述N==1的方法虽然解决了光线爆炸问题，但又有了新问题：样本数量下降，结果生成的画面噪点会变得非常多。

针对这个问题，我们可以发出多条路径穿过像素，再将这么多路径的着色结果求均值即可。

void ray_generation(camPos, pixel) {
    //在像素上均匀地选取N个样本位置
    pixel_radiance = 0.0;
    //对于每个样本位置
    For each sample in the pixel
        //发射一条射线r(CamPos, cam_to_sample)
        shoot a ray r(CamPos, cam_to_sample)
        //射线r与场景相交与点p
        IF ray r hit the scene at p
            pixel_radiance += 1 / N * shade(p, sample_to_cam)
    return pixel_radiance;
}

问题2：递归停止条件

我们都知道递归实现有两个条件：①问题得到转移；②递归要能停。第一个点刚才已经解决了，现在是要找到能停止递归的条件。

解决方法1：限制弹射递归的深度

也就是限制光线的弹射次数，这个方法意味着能量的削减，能量就不守恒了。

解决方法2：俄罗斯轮盘赌

以一定的概率停止继续追踪，想要实现追踪停止又不改变得到的结果Lo：

（1）以一定的概率P（0<P<1）发射光线 -> return Lo/P；

（2）以概率1-P不发射光线 -> return 0.

可以计算这种方式的期望值E，会发现以这种方式得到的结果还会是Lo，但无限递归的概率就收敛到0了。

$E=P*(Lo/P)+(1-P)*0=Lo$

展示成伪代码：

void shade(p, wo)
{
    //以某种方法确定一个概率P_RR
    // 随机选取一个随机数ksi∈[0,1]
    // if(ksi>P_RR) reutn 0;
    // ksi<P_RR的情况就正常发射光线，然后结果需要/P_RR
    //随机选取1个方向的wi并以pdf(wi)分布
    L0 = 0.0;
    //向该方向追踪一条射线ray r(p,wi)
    Trace a ray r(p, wi)
        //如果射线击中光源（相交）
        If ray r hit the light
        //写出求和式，这是需要/P
        Return L_i * f_r * cosine / pdf(wi) / P_RR
        //射线击中物体上的p点（射线r与q相交）
        Else if ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
}

到此为止，Path Tracing就完成了，但其实还有问题：

这个算法并不高效！It's not efficient!

问题3：目前算法并不高效

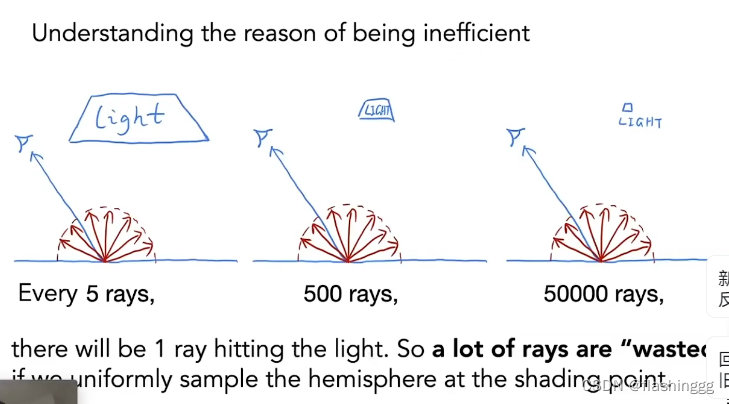
Why?

从上图可以看出，现在这种从着色点向外出射光线的采样方法，打中光源的概率完全看运气，光源面积大概率就大；光源面积小概率就小，由此可见这种方法并不高效。

需要找到另一种更高效的采样方法——采样光源 Sample the Light

问题3解决方案：采样光源Sample the light

首先要明确一点，我们为什么能改变采样方法？因为：蒙特卡洛方法并没有规定pdf的选取，我们可以选择任意一个合适的pdf进行采样！以此来大大减少光线的浪费，此时采样对象就从半球立体角dw转换到了光源表面的微面元dA：

$pdf=\frac{1}{A}$

那么随之而来又有新的问题，在之前讲蒙特卡洛方法就提到了其中一个注意点：在x上积分，就必须采样x。因此，我们需要利用数学的方法，将积分对象从dw转变到dA.

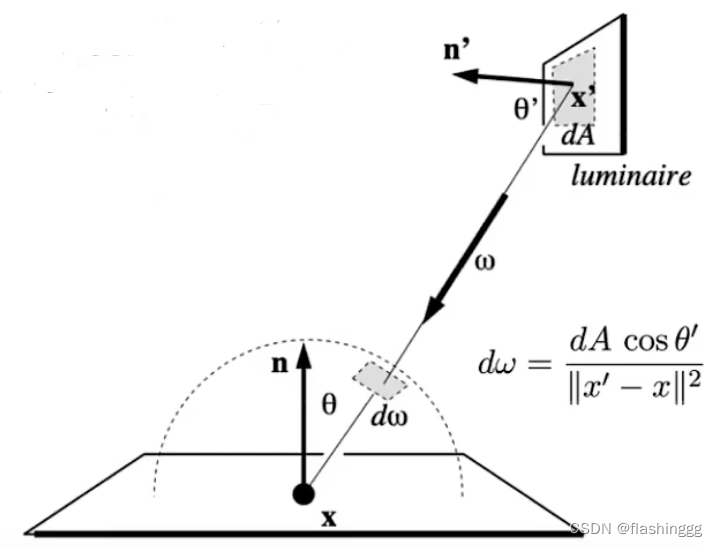
做一个变量替换，我们的渲染方程就变成了：

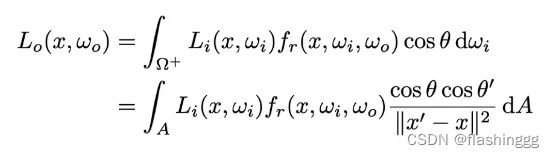
基于此，之前的算法依照全局光照的贡献对象可以分为两个部分：

（1）光照来自于光源 - 直接光照不用轮盘赌

（2）其他非光源 - 间接，需要轮盘赌

Shadow：光源遮挡问题

这个好说，直接在进行直接光照计算前判断是否被遮挡即可。

就得到了Sample the light的伪代码：

Sample the Light过程伪代码

shade (p, wo)
    //直接光照
    //在光源上均匀选择一个采样点x'，以pdf_light分布
? ? Uniformly sample the light at x' ( pdf_light = 1 / A)
? ? //首先判断光源是否被遮挡：发射一条连接物体p和x'的射线
    Shoot a ray from p to x'
    //如果射线不被遮挡，则计算直接光照：
? ? If the ray is not blocked in the middle
? ? ? ? L_dir = L_i * f_r * cos_theta * cos_theta' / |x'-p|^2 / pdf_light
    
    //间接光照
? ? L_indir = 0.0
    //以某种方法确定一个概率P_RR(0<P_RR<1)
    Test Russian Roulette with probability P_RR
    //在均匀分布在[0,1]上的样本中随机选取一个值ksi
    If ksi>P_RR
        Return L_dir;
    //半球上随机生成一个方向wi，以pdf=1/2Π分布
? ? Uniformly sample the hemisphere toward wi ( pdf_hemi = 1 / 2pi)
? ? Trace a ray r(p, wi)
    //如果射线r击中一个不自发光的物体（非光源）
? ? If ray r hit a non - emitting object at q    
? ? ? ? L_indir = shade (q, -wi) * f_r * cos_theta / pdf_hemi / P_RR

? ? Return L_dir + L_indir

Now path tracing is finally done!

把整个Path Tracing的过程学习清楚之后，已经可以开始完成作业了。但是我为了了解清楚整个代码框架每个部分是什么含义，会先把作业6和这次作业给的框架进行对比，学习并了解新增的内容都有哪些，再进行Path Tracing部分。

框架修改内容详细解读

让我们来看看都是什么地方做了改动

main.cpp

新增：定义了一些材质。

//与作业6多了部分：定义了材质（颜色）
    Material* red = new Material(DIFFUSE, Vector3f(0.0f));
    red->Kd = Vector3f(0.63f, 0.065f, 0.05f);
    Material* green = new Material(DIFFUSE, Vector3f(0.0f));
    green->Kd = Vector3f(0.14f, 0.45f, 0.091f);
    Material* white = new Material(DIFFUSE, Vector3f(0.0f));
    white->Kd = Vector3f(0.725f, 0.71f, 0.68f);
    Material* light = new Material(DIFFUSE, (8.0f * Vector3f(0.747f+0.058f, 0.747f+0.258f, 0.747f) + 15.6f * Vector3f(0.740f+0.287f,0.740f+0.160f,0.740f) + 18.4f *Vector3f(0.737f+0.642f,0.737f+0.159f,0.737f)));
    light->Kd = Vector3f(0.65f);

在作业6中并没有给模型赋予材质，而是直接给了光照，可以看到兔子是黑白的

Renderer.cpp

...   
    //出现了与作业6不同的点：加了整型变量spp
    // games101里老师提到过：“path tracing其中一个问题就是：并不高效，low spp->它的
    // spp(sample per pixel)很低，光线会被浪费”
    // 这里的spp就是指每个pixel会采样的次数
    // change the spp value to change sample ammount
    int spp = 16;
    std::cout << "SPP: " << spp << "\n";

    for (uint32_t j = 0; j < scene.height; ++j) {
        for (uint32_t i = 0; i < scene.width; ++i) {
            // generate primary ray direction
            float x = (2 * (i + 0.5) / (float)scene.width - 1) *
                      imageAspectRatio * scale;
            float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
            //这里的dir方向跟我作业6取的不一样，作业6里是(x,y,-1)
            Vector3f dir = normalize(Vector3f(-x, y, 1));
            //与作业6不同：每个pixel分成了spp次采样
            for (int k = 0; k < spp; k++){
                framebuffer[m] += scene.castRay(Ray(eye_pos, dir), 0) / spp;  
            }
            m++;
        }
...

其实这么看来，Whitted-Style Ray Tracing就相当于Path?Tracing中spp==1的情况？（不是很确定这么说是否正确）

Object.hpp?

...    
    //与6相比加了新的属性：area，以实现对光源按面积采样
    virtual float getArea()=0;
    //与6相比加了新属性：sameple
    virtual void Sample(Intersection &pos, float &pdf)=0;
    virtual bool hasEmit()=0;
...

具体涉及到的函数：

getArea()

//在Triangle.hpp & Sphere.hpp 里都有用到
float getArea(){
        return area;
}

Sample()

这个函数将会在Scene.cpp?->?sampleLight()光源采样接口函数中用到。

//class MeshTriangle里：
    void Sample(Intersection &pos, float &pdf){
        bvh->Sample(pos, pdf);
        pos.emit = m->getEmission();
    }

//class Sphere：
    void Sample(Intersection &pos, float &pdf){
        float theta = 2.0 * M_PI * get_random_float(), phi = M_PI * get_random_float();
        Vector3f dir(std::cos(phi), std::sin(phi)*std::cos(theta), std::sin(phi)*std::sin(theta));
        pos.coords = center + radius * dir;
        pos.normal = dir;
        pos.emit = m->getEmission();
        pdf = 1.0f / area;
    }

//class Triangle：
    void Sample(Intersection &pos, float &pdf){
        float x = std::sqrt(get_random_float()), y = get_random_float();
        pos.coords = v0 * (1.0f - x) + v1 * (x * (1.0f - y)) + v2 * (x * y);
        pos.normal = this->normal;
        pdf = 1.0f / area;
    }

get_random_float()

gloal.hpp中定义的一个随机从范围[0,1]取浮点数的函数：

//得到范围为[0.1]的浮点数
inline float get_random_float()
{
    std::random_device dev;
    std::mt19937 rng(dev());
    std::uniform_real_distribution<float> dist(0.f, 1.f); // distribution in range [0，1]

    return dist(rng);
}

值得注意的是！?

感谢解决了随机数的取值问题：Games101 作业7 路径追踪_gong_zi_shu的博客-CSDN博客

其中提到window系统跑这份代码的同学，需要修改global.cpp 中的get_random_float()函数，不然你的这个"随机函数"每次都是跑出来相同的结果，修改后能显著提高效率，改为：

inline float get_random_float()
{
    static std::random_device dev;
    static std::mt19937 rng(dev());
    static std::uniform_real_distribution<float> dist(0.f, 1.f); // distribution in range [0，1]

    return dist(rng);
}

经过实践这个函数确实能显著提高效率！后续会出一片作业7加速渲染的优化方法汇总，展示前后对比。

hasEmit()

//均相同，是：
    bool hasEmit(){
        return m->hasEmission();
    }
//m：
    Material* m;
//hasEmission() 是 class Material 定义的一个
    bool Material::hasEmission() {
        if (m_emission.norm() > EPSILON) return true;
        else return false;
    }

hasEmission()

?Material.hpp中定义的一bool类型：

bool Material::hasEmission() {
    if (m_emission.norm() > EPSILON) return true;//e_emission有长度，即它存在
    else return false;
}

Sphere.hpp

与作业6相比：多了一个 area属性 和一个 Sample()函数

area

...
//与作业6相比多了一个area
    float area;
    ...
    bool intersect(const Ray& ray) {
        ...
        //整个球面积=4Πr2
        float area = 4 * M_PI * radius2;
        ...
    }
...

Sample()（目前没搞明白这个函数怎么写的）

对光源采样，在上面的Object.hpp已经体现过了，这里贴一个课上老师将Sampling the light的截图帮助理解，可以结合我对代码的注释具体理解这个函数：

   //将光源进行按面采样,随机从光源发射一条ray打到场景中的sphere上得到某个交点
    void Sample(Intersection &pos, float &pdf){
        //theta(θ)∈[0,2Π]，控制着
        // 
        // 
        //phi(φ)∈[0,Π]
        float theta = 2.0 * M_PI * get_random_float(), phi = M_PI * get_random_float();
        //dir -> {cosφ,sinφ*cosθ,sinφ*sinθ}
        Vector3f dir(std::cos(phi), std::sin(phi)*std::cos(theta), std::sin(phi)*std::sin(theta));
        pos.coords = center + radius * dir;//O+dir*r
        pos.normal = dir;
        pos.emit = m->getEmission();
        pdf = 1.0f / area;//
    }

getArea() & hasEmint()

Object.hpp已有提及：

...
    float getArea(){
        return area;
    }
    bool hasEmit(){
        return m->hasEmission();
    }
...

Triangle()

与Sphere.hpp相同，给Triangle和MeshTriangle类也是加上了Area和Sample()

class Triangle : public Object
{
...
        //三角形面积
        area = crossProduct(e1, e2).norm()*0.5f;
...
    void Sample(Intersection &pos, float &pdf){
        float x = std::sqrt(get_random_float()), y = get_random_float();
        pos.coords = v0 * (1.0f - x) + v1 * (x * (1.0f - y)) + v2 * (x * y);
        pos.normal = this->normal;
        pdf = 1.0f / area;
    }
    float getArea(){
        return area;
    }
    bool hasEmit(){
        return m->hasEmission();
    }
};

...

class MeshTriangle : public Object
{
...
        area = 0;
...
    void Sample(Intersection &pos, float &pdf){
        bvh->Sample(pos, pdf);
        pos.emit = m->getEmission();
    }
    float getArea(){
        return area;
    }
    bool hasEmit(){
        return m->hasEmission();
    }
};

BVH.hpp

定义的BVH类中加上了getSample()和Sample()函数。

...    
    void getSample(BVHBuildNode* node, float p, Intersection &pos, float &pdf);
    void Sample(Intersection &pos, float &pdf);
...

BVH.cpp -> getSample()

void BVHAccel::getSample(BVHBuildNode* node, float p, Intersection &pos, float &pdf){
    if(node->left == nullptr || node->right == nullptr){
        node->object->Sample(pos, pdf);
        pdf *= node->area;
        return;
    }
    if(p < node->left->area) getSample(node->left, p, pos, pdf);
    else getSample(node->right, p - node->left->area, pos, pdf);
}

Material.hpp

实现了smple，eval，pdf三个方法用于Path Tracing变量的辅助计算，我们把这部分代码从头到尾看一遍：

首先枚举定义了一个材料类型漫反射材质，这次作业好像也只有这一个材质类型；

enum MaterialType { DIFFUSE};

接下来定义了一个类Material；

class Material{
private:

   ...

public:

   ...

};

（2）private里首先定义三个向量分别代表：反射射线方向、折射射线方向和菲涅尔方程项，都与作业5类似，就不过多赘述，具体可以去看看我写的那篇：GAMES101作业5-从头到尾理解代码&Whitted光线追踪_flashinggg的博客-CSDN博客

...
Vector3f reflect(const Vector3f &I, const Vector3f &N) const
    {
        return I - 2 * dotProduct(I, N) * N;
    }

    //折射射线方向，与作业5相同
    Vector3f refract(const Vector3f &I, const Vector3f &N, const float &ior) const
    {
        ...
    }
    
    //菲涅尔方程，与作业5相同
    void fresnel(const Vector3f &I, const Vector3f &N, const float &ior, float &kr) const
    {
        ...
    }
...

toWorld()

接着加了一个作业5中没有的向量toWorld，作用是将localray的半球坐标（局部）变换成世界坐标.，具体过程可以参考我的代码注释：

...
    // 半球坐标 -> 世界坐标
    // 半球上的坐标是局部坐标系下的a，认为法向量是N方向上的(0,0,1)，所以需要转换
    // 其中局部坐标系下：a.x,a.y,a.z在的三个方向相互垂直，其中a.z的方向就是N的方向
    // 步骤：
    // 1.假定有B,C两个单位向量，B,C由N得出，B,C,N两两垂直，且B,C,N都是单位向量
    // 2.让a.x,a.y,a.z的值分别去乘B,C,N ->沿着B,C,N三个方向按照对应值的比例放大
    // 3.再将得到的三个向量相加，就能在世界坐标中出表示出原始的a
    Vector3f toWorld(const Vector3f &a, const Vector3f &N){
        //假定B,C
        Vector3f B, C;
        //这里的条件判断，应该是为了避免出现分母为0的情况
        if (std::fabs(N.x) > std::fabs(N.y)){//至少在x轴上有分量
            float invLen = 1.0f / std::sqrt(N.x * N.x + N.z * N.z);
            //我们就不管y轴的事（已知x一定有值）
            //保证以下两点：1.用x,z的数表示出一个单位向量；2.且要与N垂直
            C = Vector3f(N.z * invLen, 0.0f, -N.x *invLen);
        }
        //这里同理，只不过用的是y,z的数表示了
        else {
            float invLen = 1.0f / std::sqrt(N.y * N.y + N.z * N.z);
            C = Vector3f(0.0f, N.z * invLen, -N.y *invLen);
        }
        //按照步骤1，C,N做叉乘得到与C,N都垂直的单位向量B
        B = crossProduct(C, N);
        //进行步骤2，分别相乘，再加在一起（步骤3）
        return a.x * B + a.y * C + a.z * N;
    }
...

至于半球坐标的计算sample()在后面会将到，我们继续顺着代码看，下面是public，我做了一些简单的小注释帮助理解代码。

...
public:
    MaterialType m_type;//材质类型，只给了一个枚举项：diffuse
    //Vector3f m_color;
    Vector3f m_emission;//材质自发光
    float ior;//材质的折射率
    Vector3f Kd, Ks;//漫反射和高光项
    float specularExponent;//高光项指数
    //Texture tex;

    inline Material(MaterialType t=DIFFUSE, Vector3f e=Vector3f(0,0,0));//这里e_type=diffuse, e_emission=e
    inline MaterialType getType();//return m_type
    //inline Vector3f getColor();
    inline Vector3f getColorAt(double u, double v);//返回当下的vector3f？
    inline Vector3f getEmission();//return m_emission
    inline bool hasEmission();//判断是否有emission

    //光线击中某点后，继续随即弹射的方向
    inline Vector3f sample(const Vector3f &wi, const Vector3f &N);
    //计算该光线的pdf（概率密度函数probability density function，描述连续随机变量的概率分布）
    inline float pdf(const Vector3f &wi, const Vector3f &wo, const Vector3f &N);
    //计算光线的贡献
    inline Vector3f eval(const Vector3f &wi, const Vector3f &wo, const Vector3f &N);
...

sample()

下面是class里定义涉及到的一些函数，其中sample()用于采样光线击中某点后继续随机弹射的方向：——

//采样光线击中某点后继续随机弹射的方向
Vector3f Material::sample(const Vector3f &wi, const Vector3f &N){
    switch(m_type){
        case DIFFUSE:
        {
            // 均匀地对半球采样
            //半球z轴值z∈[0,1]
            // r -> 以法线为旋转轴的半径,x2+y2+z2=1，r2=x2+y2
            //phi∈[0,2Π]，旋转角度
            float x_1 = get_random_float(), x_2 = get_random_float();//随机[0,1]取值
            float z = std::fabs(1.0f - 2.0f * x_1);//不是很理解为什么不直接取[0,1]随机数
            float r = std::sqrt(1.0f - z * z), phi = 2 * M_PI * x_2;
            Vector3f localRay(r*std::cos(phi), r*std::sin(phi), z);//半球面上随机光线的方向
            //接着需要把半球上的局部光线坐标转换成世界坐标
            return toWorld(localRay, N);
            break;
        }
    }
}

pdf()

概率密度函数的计算，可以来回顾一下pdf的定义，帮助更好的理解代码：

PDF

参考：03.随机变量和3F（PDF、CDF、PMF） - 知乎 (zhihu.com)

概率密度函数（probability density function），用来描述连续随机变量的概率分布，连续型随机变量的概率密度函数是一个描述某个确定的取值点附近的可能性的函数。

例如：正态分布的PDF：

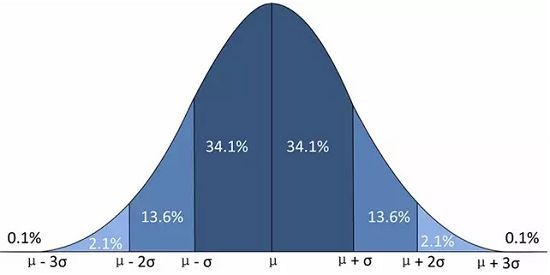
计算ray的PDF:

如上图：课程里老师给出了一个简单的采样方法——均匀地采样

pdf就是个常数，整个半球面对应的Solid angle： $2\pi$ ，均匀的采样pdf就是： $1/2\pi$

//计算概率密度函数pdf
float Material::pdf(const Vector3f &wi, const Vector3f &wo, const Vector3f &N){
    switch(m_type){
        case DIFFUSE://材质
        {
            //均匀采样，则pdf为常数1/2Π
            if (dotProduct(wo, N) > 0.0f)
                return 0.5f / M_PI;
            else
                return 0.0f;
            break;
        }
    }
}

eval()

计算某个材质对光照的贡献，本作业用漫反射系数kd来体现：

//计算材质贡献
Vector3f Material::eval(const Vector3f &wi, const Vector3f &wo, const Vector3f &N){
    switch(m_type){
        case DIFFUSE:
        {
            //计算DIFFUSE贡献 -> kd 
            float cosalpha = dotProduct(N, wo);//只看半球，另一半不看，所以要判断一下wo和N的夹角
            if (cosalpha > 0.0f) {
                Vector3f diffuse = Kd / M_PI;
                return diffuse;
            }
            else
                return Vector3f(0.0f);
            break;
        }
    }
}

Material.hpp到这里就结束了。

补全castRay()

粘贴作业6代码

粘贴需要注意的点

代码其他的部分直接粘贴作业6的内容，直接粘贴就好但有两点值得注意：

（1）Intersectp()函数注意取等号问题：

...
return tenter <= texit&& texit >= 0;
...

原因在games101学习平台有大神给了解释：Games101 作业7 绕坑引路 (Windows) – 计算机图形学与混合现实在线平台 (games-cn.org)

（2）为了大幅度缩短渲染时长，建议在运行代码前修改get_random_float()函数，这点在上面的代码注释中已有提到，这里就只展示修改后的：

inline float get_random_float()
{
    static std::random_device dev;
    static std::mt19937 rng(dev());
    static std::uniform_real_distribution<float> dist(0.f, 1.f); // distribution in range [0，1]

    return dist(rng);
}

Bounds3.hpp -> IntersectP()

inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
                                const std::array<int, 3>& dirIsNeg) const
{
    Vector3f tmin = (pMin - ray.origin) * invDir;
    Vector3f tmax = (pMax - ray.origin) * invDir;
    if (dirIsNeg[0])
        std::swap(tmin.x, tmax.x);
    if (dirIsNeg[1])
        std::swap(tmin.y, tmax.y);
    if (dirIsNeg[2])
        std::swap(tmin.z, tmax.z);
    float texit = std::min(tmax.x, std::min(tmax.y, tmax.z));
    float tenter = std::max(tmin.x, std::max(tmin.y, tmin.z));
    return tenter <= texit&& texit >= 0;
}

?Triangle.hpp -> getIntersection(Ray ray)

inline Bounds3 Triangle::getBounds() { return Union(Bounds3(v0, v1), v2); }

inline Intersection Triangle::getIntersection(Ray ray)
{
    Intersection inter;

    if (dotProduct(ray.direction, normal) > 0)
        return inter;
    double u, v, t_tmp = 0;
    Vector3f pvec = crossProduct(ray.direction, e2);
    double det = dotProduct(e1, pvec);
    if (fabs(det) < EPSILON)
        return inter;

    double det_inv = 1. / det;
    Vector3f tvec = ray.origin - v0;
    u = dotProduct(tvec, pvec) * det_inv;
    if (u < 0 || u > 1)
        return inter;
    Vector3f qvec = crossProduct(tvec, e1);
    v = dotProduct(ray.direction, qvec) * det_inv;
    if (v < 0 || u + v > 1)
        return inter;
    t_tmp = dotProduct(e2, qvec) * det_inv;

    if (t_tmp < 0)//t>0 ray是射线
        return inter;

    // TODO find ray triangle intersection
    //给inter所有参数赋予值
    inter.happened = true;//有交点
    inter.coords = ray(t_tmp);//vector3f operator()(double t){return origin+dir*t};
    inter.normal = normal;//法向量
    inter.distance = t_tmp;//double distance
    inter.obj = this;//this是所有成员函数的隐藏函数，一个const指针，指向当前对象（正在使用的对象）
    inter.m = m;//class 材质 m
    return inter;
}

?BVH.hpp ->?getIntersection()

Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
    Intersection res;
    std::array<int, 3>dirIsNeg = { int(ray.direction.x<0), int(ray.direction.y<0), int(ray.direction.z<0) };
    //无交点
    if (!node->bounds.IntersectP(ray, ray.direction_inv, dirIsNeg)) {
        return res;
    }
    //有交点
    //无子节点
    if (node->left == nullptr && node->right == nullptr) {
        res = node->object->getIntersection(ray);
        return res;
    }
    //有子节点 ->递归
    Intersection left, right;
    left = getIntersection(node->left, ray);
    right = getIntersection(node->right, ray);
    return left.distance < right.distance ? left : right;
}

下面参考作业给出的伪代码补全castRay()。

本次实验给出的与框架匹配的伪代码

shade (p, wo)
? ? sampleLight ( inter , pdf_light )
? ? Get x, ws , NN , emit from inter
? ? Shoot a ray from p to x
? ? If the ray is not blocked in the middle
? ?     L_dir = emit * eval(wo , ws , N) * dot(ws , N) * dot(ws , NN) / |x-p|^2 / pdf_light
? ? 
    L_indir = 0.0
? ? Test Russian Roulette with probability RussianRoulette
? ? wi = sample (wo , N)
? ? Trace a ray r(p, wi)
? ? If ray r hit a non - emitting object at q
? ? ? ? L_indir = shade (q, -wi) * eval (wo , wi , N) * dot(wi , N) / pdf(wo , wi , N) / RussianRoulette
? ? 
    Return L_dir + L_indir

简单分析一些新出现的函数

Scene::sampleLight()

伪代码第一步是sampleLight()函数，这个函数在Scene.cpp中定义的，是实现采样光源的接口。

//实现了采样光源的接口
//对场景中的光源进行随机采样，以pdf进行
void Scene::sampleLight(Intersection& pos, float& pdf) const
{
    float emit_area_sum = 0;
    for (uint32_t k = 0; k < objects.size(); ++k) {
        if (objects[k]->hasEmit()) {//第k个物体有自发光，hasEmit ->bool量
            emit_area_sum += objects[k]->getArea();//得到场景中自发光区域的面积和，用以后续求pdf=1/area
        }
    }
    //对场景中的所有光源按面积均匀采样一个点，计算
    float p = get_random_float() * emit_area_sum;//随机取[0, emit_area_sum]之间的浮点数
    emit_area_sum = 0;
    for (uint32_t k = 0; k < objects.size(); ++k) {
        if (objects[k]->hasEmit()) {
            emit_area_sum += objects[k]->getArea();
            if (p <= emit_area_sum) {//随机选取一个光源面，即第k个自发光物体的光源面
                //利用Sample()在光源面中按照pdf的概率随即找到一个点pos，得到这个点pos的信息
                objects[k]->Sample(pos, pdf);
                break;
            }
        }
    }
}

代码具体实现过程

步骤我已经尽可能的在注释写的很详细了，直接看代码：

// Implementation of Path Tracing
Vector3f Scene::castRay(const Ray& ray, int depth) const
{
    //创建变量以储存直接和间接光照计算值
    Vector3f dir = { 0.0,0.0,0.0 };
    Vector3f indir = { 0.0,0.0,0.0 };
    //1.判断是否有交点：光线与场景中物体相交？
    Intersection inter = Scene::intersect(ray);
    //如果没交点
    if (!inter.happened) {
        return dir;//return 0,0,0
    }
    //2.ray打到光源了：说明渲染方程只用算前面的自发光项，因此直接返回材质的自发光项
    if (inter.m->hasEmission()) {
        if (depth == 0) {//第一次打到光
            return inter.m->getEmission();
        }
        else return dir;//弹射打到光，直接返回0，0.0

    }
    //3.ray打到物体：这个时候才开始进行伪代码后面的步骤
    
    //对场景中的光源进行采样，得到采样点light_pos和pdf_light
    Intersection light_pos;
    float pdf_light = 0.0f;
    sampleLight(light_pos, pdf_light);
   
    //3.1计算直接光照

    //物体的一些参数
    Vector3f p = inter.coords;
    Vector3f N = inter.normal.normalized();
    Vector3f wo = ray.direction;//物体指向场景
    //光源的一些参数
    Vector3f xx = light_pos.coords;
    Vector3f NN = light_pos.normal.normalized();
    Vector3f ws = (p - xx).normalized();//光源指向物体
    float dis = (p - xx).norm();//二者距离
    float dis2 = dotProduct((p - xx), (p - xx));

    //判断光源与物体间是否有遮挡：
    //发出一条射线，方向为ws 光源xx -> 物体p
    Ray light_to_obj(xx, ws);//Ray(orig,dir)
    Intersection light_to_scene = Scene::intersect(light_to_obj);
    //假如dis>light_to_scene.distance就说明有遮挡，那么反着给条件即可：
    if (light_to_scene.happened&& (light_to_scene.distance-dis>-EPSILON)) {//没有遮挡
        //为了更贴近伪代码，先设定一些参数
        Vector3f L_i = light_pos.emit;//光强
        Vector3f f_r = inter.m->eval(wo, -ws, N);//材质，课上说了，BRDF==材质，ws不参与计算
        float cos_theta = dotProduct(-ws, N);//物体夹角
        float cos_theta_l = dotProduct(ws, NN);//光源夹角
        dir = L_i * f_r * cos_theta * cos_theta_l / dis2 / pdf_light;
    }

    //3.2间接光照
    
    //俄罗斯轮盘赌
    //Scene.hpp中已经定义了P_RR:RussianRoulette=0.8
    float ksi = get_random_float();//随机取[0,1]
    if (ksi < RussianRoulette) {
        //计算间接光照
        
        //随机生成一个wi方向
        Vector3f wi = inter.m->sample(wo, N).normalized();//这里的wi其实没参与计算，返回的是一个随机的方向
        Ray r(p, wi);
        Intersection obj_to_scene = Scene::intersect(r);
        //击中了物体&&物体不是光源
        if (obj_to_scene.happened && !obj_to_scene.m->hasEmission()) {
            Vector3f f_r = obj_to_scene.m->eval(wo, wi, N);//wo不参与计算
            float cos_theta = dotProduct(wi, N);
            float pdf_hemi = obj_to_scene.m->pdf(wo, wi, N);
            indir = castRay(r, depth + 1) * f_r * cos_theta / pdf_hemi / RussianRoulette;
        }
    }
    return dir + indir;
}