文章目录
1、位图
1.1 位图的基本概念
位图是一种非常常用的数据结构,本质其实是一个二进制数组。位图和哈希表类似,都是进行映射,但又有不同。位图的每一位都用于表示数据的某种状态,例如存在或者不存在,并不表示数据本身。而哈希表时用来存放关键字key。位图更加适用于海量数据处理及分析。
位图判断数据是否存在,则有两种状态,存在和不存在,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在,相当于哈希表的直接定址法。比如:
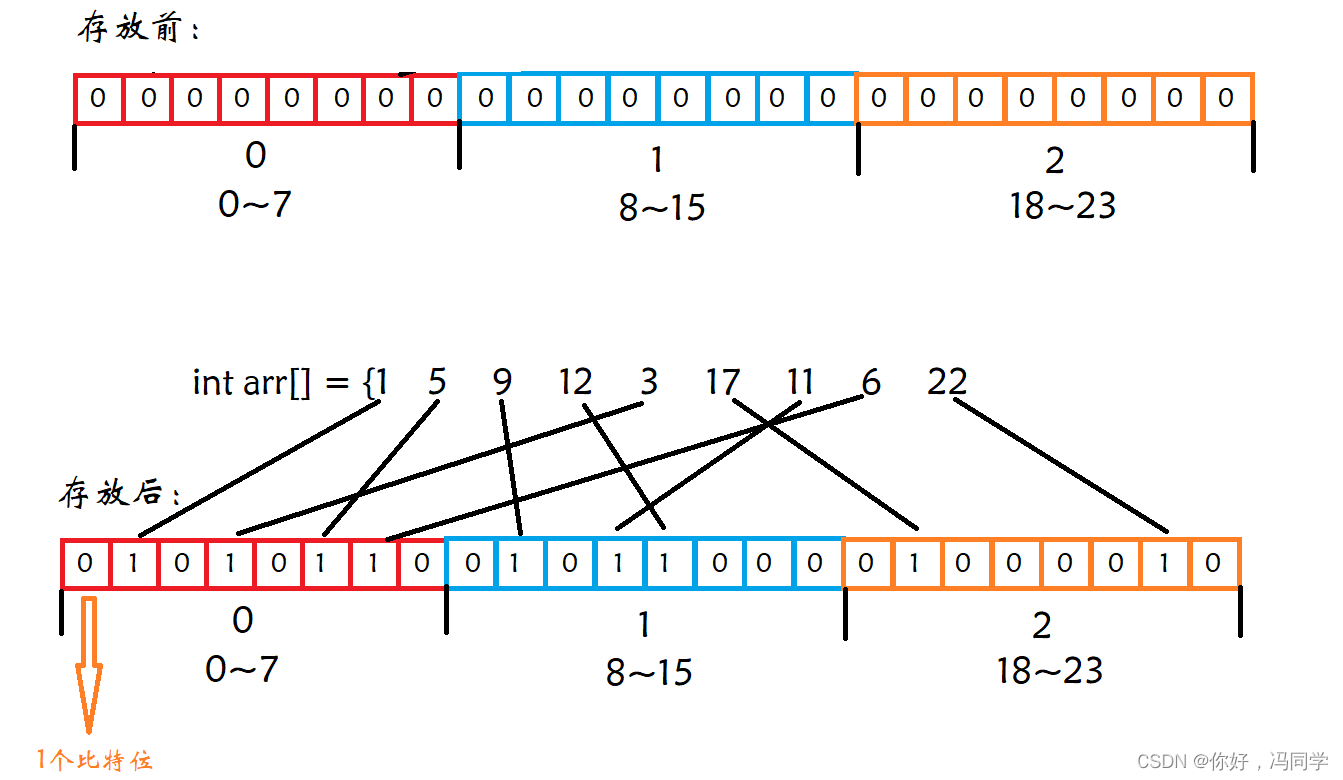
1.2 位图的实际应用
- 快速查找某个数据是否在一个集合中
- 排序
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中
方法1:遍历,时间复杂度O(N)
方法2:排序(O(Nlog2N)),利用二分查找: log2N
方法3:位图解决
方法1和方法2很简单,此时就不在进行过多赘述。
主要来看一下方法3:首先我们需要知道无符号整数表达的最大值为4294967295,虽然有40亿个数,但很多数都是重复的,也不会超过这个最大值。为了保证在无符号整数范围内每个数都不发生冲突,位图就需要4294967295比特位,最终换算相当于需要511M内存空间,对于现在的普通计算机而言,是完全可以承受的。空间开辟好后,对这40亿个数进行一一映射,将相应的比特位置为1即可。至于如何操作,请看后文。
1.3 位图的实现
template<size_t N>
class Biteset
{
public:
Biteset()
{
_bits.resize(N / 8 + 1, 0);//每次都要多开一个,例如需要表示0-16,需要17个比特位
}
//将n所对应的比特位置为1
void set(size_t n)
{
size_t i = n / 8;
size_t j = n % 8;
_bits[i] |= (1 << j);//将对应的位置位1
}
//将n所对应的比特位置为0
void reset(size_t n)
{
size_t i = n / 8;
size_t j = n % 8;
_bits[i] &= (~(1 << j));//将对应的位置位0
}
//判断一个数是否存在
bool exist(size_t n)
{
size_t i = n / 8;
size_t j = n % 8;
return (_bits[i] & (1 << j));
}
std::vector<char> _bits;
};
因为C++申请空间不能按比特位的个数进行申请,只能按单个字节的整数倍进行申请。所以我们申请一个类型为char的vector,每一个char都有8个比特位,就能够表示8个数的存在状态。
在每个成员函数中,i都表示vector中第几个char(字节),j表示这个char(字节)的第几个比特位。对此可以进行画图分析:
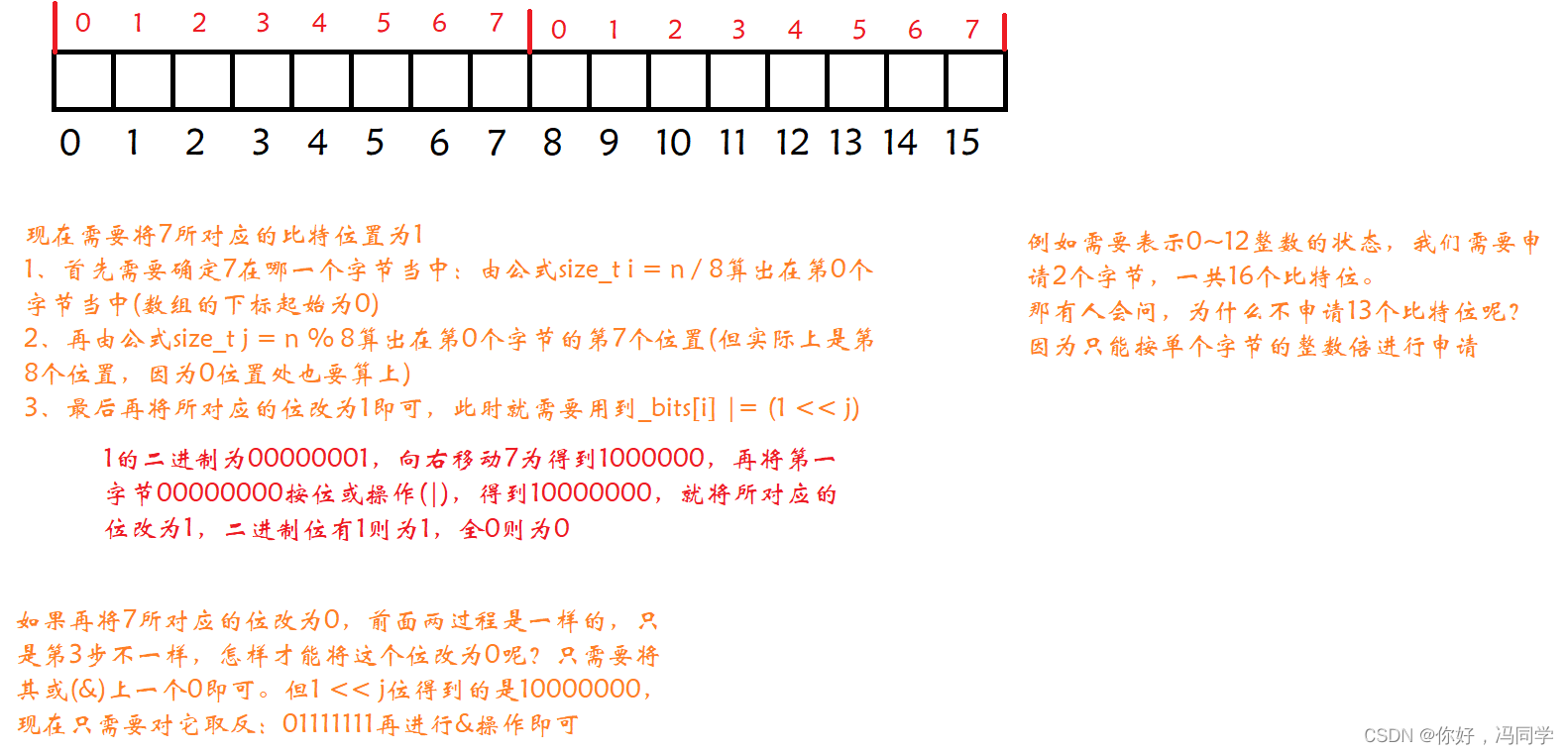
代码测试:
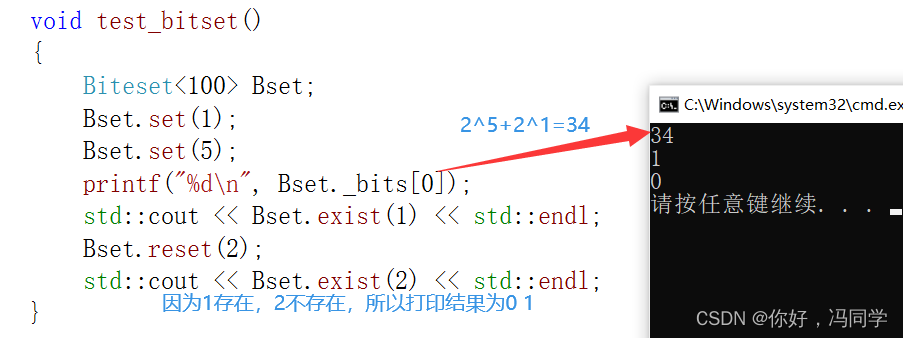
void test_bitset()
{
Biteset<100> Bset;
Bset.set(1);
Bset.set(5);
printf("%d\n", Bset._bits[0]);
std::cout << Bset.exist(1) << std::endl;
Bset.reset(2);
std::cout << Bset.exist(2) << std::endl;
}
上面的位图只适用于存在或者不存在两种状态,那怎么表示多种状态呢?有这么一道题:给定100亿个整数,设计算法找到只出现一次的整数。所以某个数可能出现2次、3次或者多次,此时就需要对位进行扩展。
template<size_t N>
class TowBiteSet
{
public:
void Set(size_t n)
{
//00 ---- 01
if (!_bit1.exist(n) && !_bit2.exist(n))
{
_bit2.set(n);
}
//01 ---- 10
else if (!_bit1.exist(n) && _bit2.exist(n))
{
_bit1.set(n);
_bit2.reset(n);
}
//10表示出现两次或者两次以上,不需要处理
}
void PrintOnceNum()
{
for (size_t i = 0; i < N; ++i)
{
if (!_bit1.exist(i) && _bit2.exist(i))//01
cout << i << " ";
}
cout << endl;
}
private:
fl::Biteset<N> _bit1;//表示第二位
fl::Biteset<N> _bit2;//表示第一位
};
如果一个数所对应的为01,那么它再次出现时,需要将对应的位改为10,其实类似于进位操作。
代码测试:
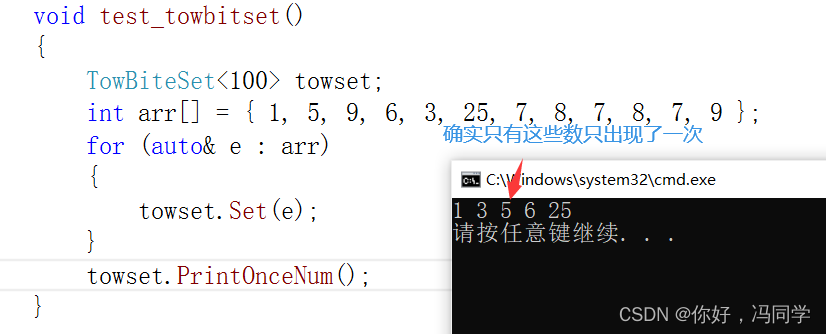
void test_towbitset()
{
TowBiteSet<100> towset;
int arr[] = { 1, 5, 9, 6, 3, 25, 7, 8, 7, 8, 7, 9 };
for (auto& e : arr)
{
towset.Set(e);
}
towset.PrintOnceNum();
}
2、布隆过滤器
2.1 什么是布隆过滤器
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
位图只能用于整数的状态判断,如果需要判断小数或者字符串的状态呢?此时就需要用到布隆过滤器。那怎么实现的呢?粗略的讲就是将数据通过单个或者多个哈希函数映射到单个或多个位上。
2.2 布隆过滤器的优缺点
优点:
- 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 哈希函数相互之间没有关系,方便硬件并行运算
- 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
缺点:
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
- 如果采用计数方式删除,可能会存在计数回绕问题
2.3 布隆过滤器的使用场景
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那些已经存在的记录,对于这样的场景就使用到了布隆过滤器。类似的还有:
- 邮件过滤,使用布隆过滤器来做邮件黑名单过滤
- 对爬虫网址进行过滤,爬过的不再爬
- 抖音、快手等短视频,刷到过的视频不会再被二次刷到
- 注册时,需要填写昵称,判断该昵称是否被其他用户使用
- 一些数据库内置布隆过滤器,用于判断数据是否存在,可以减少数据库的IO请求,从而提高性能
2.4 布隆过滤器的原理
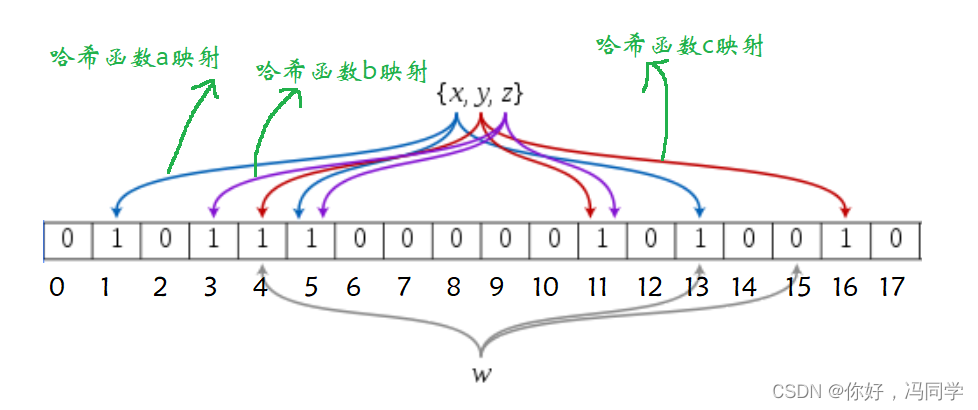
布隆过滤器实际上是一个二进制数组加上多个随机的哈希函数。将数据通过哈希函数计算映射到对应的比特位中。如果对应的比特位已经被置为1,那么就通过另外一个哈希函数计算映射到另一个比特位,但哈希函数的个数是有限的,因此在判断数据的状态时会存在一定的误判。
如下就是一个简单的布隆过滤器示意图:
2.5 布隆过滤器的误判
假设现在需要判断一个数据a和数据b是否存在,假设a通过哈希函数a,b,c映射到了位置3、位置5和位置13,这三个位置的状态都为存在,此时我们就认为数据a存在,但实际上是不存在的,这就是布隆过滤器的误判行为。假设b通过哈希函数a,b,c映射到了位置7、位置8和位置9,这三个位置的状态都为不存在,那么数据b肯定不存在。
所以:对于数据存在可能会存在误判,对于数据不存在,一定不会存在误判
布隆过滤器的误判是无法避免的,但是可以通过多种手段将误判率降低,比如布隆过滤器的长度,增加哈希函数的个数来映射多个位置。那么到底如何权衡布隆过滤器的长度和哈希函数的个数呢?有人通过计算给出了这么一个公式:

k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率。
虽然影响误判率的因素有3个,但我觉得最影响的还是布隆过滤器的长度
为什么是这样,本人学识浅薄,并不知道其中的奥秘。
2.6 布隆过滤器的实现
#pragma once
#include<bitset>
#include<string>
#include<iostream>
using namespace std;
//哈希函数1
struct BKDRHash
{
size_t operator()(const string& s)
{
//BKDR哈希
size_t value = 0;
for (auto ch : s)
{
value *= 31;
value += ch;
}
return value;
}
};
//哈希函数2
struct APHash{
size_t operator()(const string& s)
{
size_t hash = 0;
for (long i = 0; i < s.size(); i++)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
}
}
return hash;
}
};
//哈希函数3
struct DJBHash{
size_t operator()(const string& s)
{
size_t hash = 5381;
for (auto ch : s)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
template<size_t N,
class K = string,
class HashFunc1 = BKDRHash,
class HashFunc2 = APHash,
class HashFunc3 = DJBHash>
class BloomFilter
{
public:
void Set(const K& key)
{
size_t len = 4 * N;
size_t index1 = HashFunc1()(key) % len;
size_t index1 = HashFunc2()(key) % len;
size_t index1 = HashFunc3()(key) % len;
_bs.set(index1);
_bs.set(index2);
_bs.set(index3);
}
//判断数据是否存在,存在可能会有误判
void Test(const K& key)
{
size_t len = 4 * N;
size_t index1 = HashFunc1()(key) % len;
if (_bs.test(index1) == false)
return false;
size_t index2 = HashFunc2()(key) % len;
if (_bs.test(index2) == false)
return false;
size_t index3 = HashFunc3()(key) % len;
if (_bs.test(index3) == false)
return false;
//当3个位置都存在时才存在,但是可能会误判
return true;
}
private:
bitset<4*N> _bs;//根据前面的公式可以算出1个数据对应4个比特位
};
这里我们没有写删除,为什么呢?请看下图:
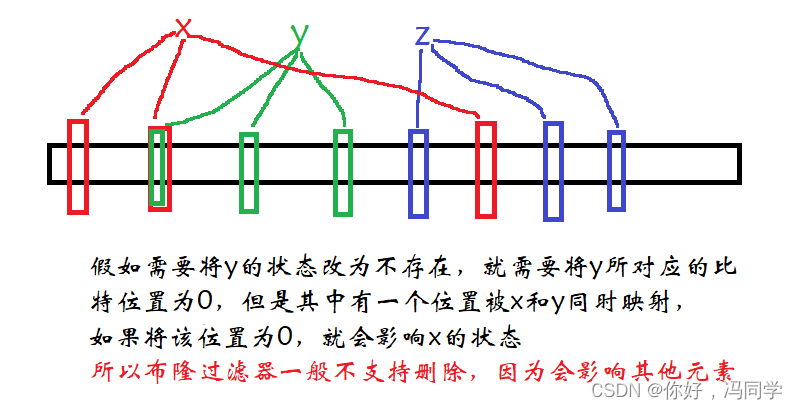
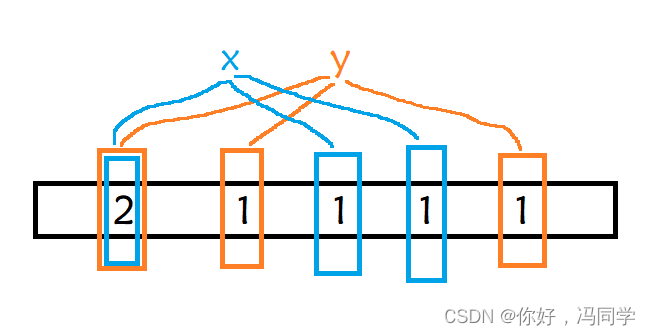
如果要实现删除也不是不行。使布隆过滤器的每个标记位用多个比特位表示,用来计算有多少个数据映射到该位,相当于引用计数。但整体而言,消耗的空间也就变多了,布隆过滤器的优势也下降了。
3、哈希切分
给定两个文件A和B,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?请给出精确算法
假如这100亿个query的大小为100个G,两个文件加起来就200个G
方法1:将每个文件分为大小相等的200个小文件,每个小文件占500M,将A
中的小文件分别和B中的小文件进行一一求交集,那么将求20100(200+199+…+2+1)次,计算量也是相当庞大,主要原因还是相同的query可能在不同的小文件中,例如一个在A1中,一个在B10中。
方法2:对于方法1的情况,可以使用哈希切分。将相近的query放在编号相同的小文件中,这样只需要A1和B1比较,A2和B2比较…一共只需要比较200次即可。
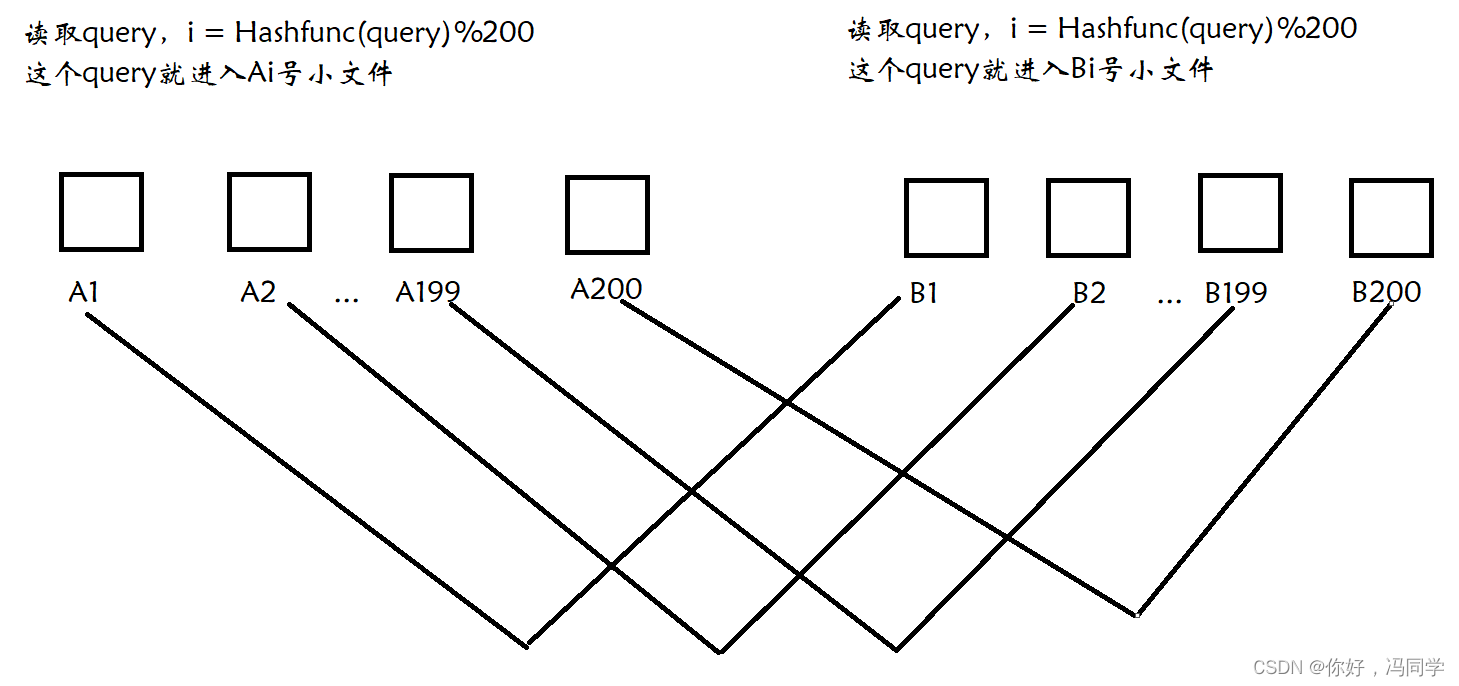
但这样还存在一个问题,就是单个文件太大,可能会超过1G,那么此时就需要换个哈希函数再切分,直到满足不再超过1G为止。