我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为 B 串,全“1”串称为 I 串,既含“0”又含“1”的串则称为 F 串。
FBI 树是一棵二叉树,它的结点类型也包括 F 结点,B 结点和 I 结点三种。由一个长度为 2N 的“01”串 S 可以构造出一棵 FBI 树 T,递归的构造方法如下:
(1) T 的根结点为 R,其类型与串 S 的类型相同;
(2) 若串 S 的长度大于 1,可将串 S 从中间分开,分为等长的左右子串 S1 和 S2;由左子串 S1 构造 R 的左子树 T1,由右子串 S2 构造 R 的右子树 T2。
现在给定一个长度为 2^N 的“01”串,请用上述构造方法构造出一棵 FBI 树,并输出它的后序遍历序列。
题目大意就是给定一个序列,就比如10001011,我们将这个序列一直从中间分开,左边为左子树,右边为右子树,根据每一段全0全1还是10都有得到值F、B、I,构建成一棵二叉树,并且倒序输出。
第一种做法 队列
如何得到一个二叉树的后序输出?
我们只需要得到这颗二叉树的层次遍历放在一个数组中即可,后序遍历代码如下
(大致思路就是先判断左子树是否存在,如果存在就遍历,然后遍历右子树,最后输出根节点)
void postOrder(int root) {
int lChild = root*2;
int rChild = root*2+1;
if(lChild<=cnt) postOrder(lChild);
if(rChild<=cnt) postOrder(rChild);
cout<<e[root];
}
现在我们只需要得到这个二叉树的层次遍历数组即可
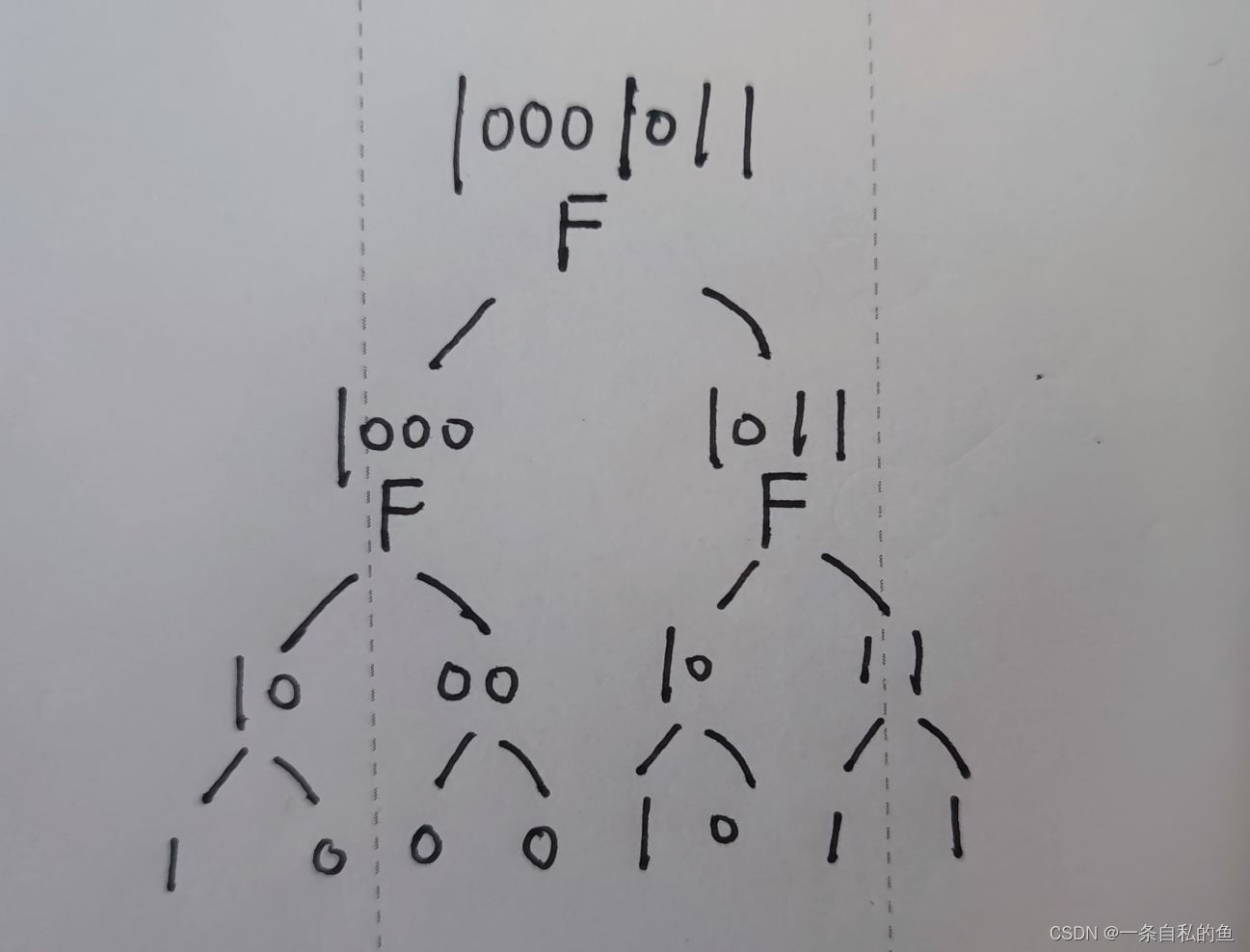
对于一开始这个序列,我们从中间分开,也就是分成1000 和 1011两部分,最开始这个既有0又有1,所以根节点是F,F的左子树是1000也就是F,右子树1011也是F,我们将这三个值依次存到层次遍历数组中。
接下来我们要遍历左子树分开两部分的值,注意如果是层次遍历的话,我们不能简单的用递归来解决,如果用递归的话,我们会一直递归到最深的那个叶节点之后再开始向右。
如下图,我们需要依次将10 00 10 11的值放入层次遍历数组,但是如果我们使用递归来解决两个范围的话,类似如下图中的代码,我们会先解决左边部分再解决右边部分。第一次分成10和00,然后进入10分成1 和 0存进数组之后出来进入右边的00,然后再进去存放两个0。
然而我们的需求是先把1000分开成两个值存入数组之后直接遍历1011,而不是继续遍历1000的子树,子树部分我们应该放在下一个范围解决
func(l,(l+r)/2);
func((l+r)/2,r);
那么该怎么解决这个问题呢
我们分成1000和1011之后,不是要将这两个范围继续分小,然后存入层次遍历数组吗?那么我们可以将没有处理的存到一个数据结构中,1000分成10和00之后,我们暂时不处理这两个范围,将他们存入数据结构留到后面处理。
那么哪种数据结构适合存放数据呢,我们来思考一下存放的特点,先存进去的先处理,后存进去的后处理,而这刚好符合一种数据结构——队列,对于1000和1011,我们先处理1000,分成两部分10和00之后,我们暂时不处理这两个范围,将他们存入队列,之后再处理1011,分成10和11之后同理也是存入队列,这时队列的结构是这样的
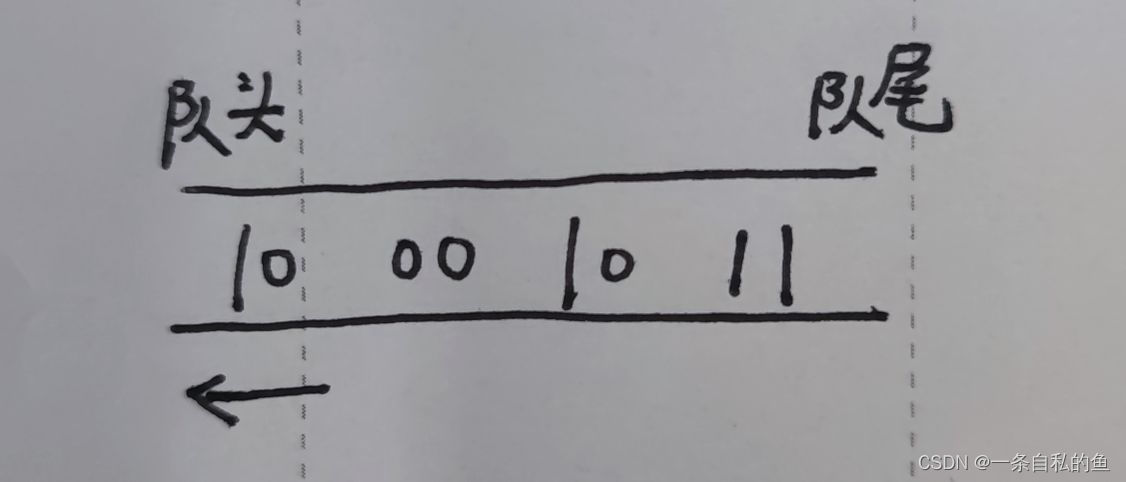
分别将这四个对应的字母10(F) 00(B) 10(F) 11(I)存入层次遍历数组之后,我们从队首取得10,然后做进一步的处理,将处理之后的值继续存入队列表明下一层要处理的范围。
就这样直到队列中没有一个元素表明这颗FBI树已经全部构造完成,那么相应的层次遍历数组也得到了,我们再用上面的代码输出这棵树的后序即可
分析代码
对于队列,你可以使用stl库中的队列,在这里我自己用数组模拟了一个队列,当然你也可以手写一个队列
我们将最开始的范围也就是从1到2^N存入队列,这也是我们要处理的第一个元素
head指向我们当前队列的头部,tail是我们队列的尾部,也就是目前最后要处理的一个数据,队列从0开始计数,tail的位置没有数据,对于每一个范围有一个左边界一个有边界,所以我们定义一个结构体,每次把这个结构体存入队列
struct node {
int l,r;
}queue[10020];
int head=-1;
int tail=1;
queue[++head].l = l;
queue[head].r = r;
只要当前队列有元素我们就需要处理,所以循环的退出条件为head==tail(表明队列头已经到队列尾空的地方)
每次用head取到当前队列的头部,zero和one用来判断这个范围是全1还是全0(如果中间有一个1,那么全0 zero就为假,如果中间有一个0,那么全1 one就为假,最后如果两个都为假说明两个都有即为F,I和B依次类推)
处理完这个范围之后,我们将这个数据排出队列,然后插入层次遍历数组(cnt表示当前遍历数组的个数,初始为0),也就是head++,如果这个范围下面有子范围,那么我们将子范围分成两个部分继续插入队列尾部
bool zero,one;
while(head < tail) {
xl = queue[head].l;
xr = queue[head].r;
zero = true;
one = true;
for(int i=xl;i<=xr;i++) {
if(t[i]=='1') zero = false;
else if(t[i]=='0') one = false;
}
if(!zero&&!one) {
e[++cnt] = 'F';
}
else if(one&&!zero) {
e[++cnt] = 'I';
}
else if(zero&&!one) {
e[++cnt] = 'B';
}
head++;
if(xl<xr) {
queue[tail].l = xl;
queue[tail++].r = (xl+xr)/2;
queue[tail].l = (xl+xr)/2+1;
queue[tail++].r = xr;
}
}
得到层次遍历数组之后我们直接后序遍历即可
完整代码如下
#include<iostream>
#include<cmath>
using namespace std;
int n,cnt;
char e[10020];
char t[1050];
struct node {
int l,r;
}queue[10020];
void postOrder(int root) {
int lChild = root*2;
int rChild = root*2+1;
if(lChild<=cnt) postOrder(lChild);
if(rChild<=cnt) postOrder(rChild);
cout<<e[root];
}
void FBI(int l,int r) {
int head=-1;
int tail=1;
queue[++head].l = l;
queue[head].r = r;
int xl,xr;
bool zero;
bool one;
while(head < tail) {
xl = queue[head].l;
xr = queue[head].r;
zero = true;
one = true;
for(int i=xl;i<=xr;i++) {
if(t[i]=='1') zero = false;
else if(t[i]=='0') one = false;
}
if(!zero&&!one) {
e[++cnt] = 'F';
}
else if(one&&!zero) {
e[++cnt] = 'I';
}
else if(zero&&!one) {
e[++cnt] = 'B';
}
head++;
if(xl<xr) {
queue[tail].l = xl;
queue[tail++].r = (xl+xr)/2;
queue[tail].l = (xl+xr)/2+1;
queue[tail++].r = xr;
}
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=pow(2,n);i++) {
cin>>t[i];
}
FBI(1, pow(2,n));
postOrder(1);
return 0;
}
第二种做法 递归
我们为什么要先得到层次遍历数组之后再后序遍历呢?为什么题目中让我们直接输出后序遍历呢?
对于一个FBI树,如果要得到后序遍历,我们当然是先处理左节点之后处理右节点,最后处理根节点,这就是后序遍历 而刚好我们构建这颗FBI树的时候不也是递归先处理左子节点,再处理右子节点之后再处理自身吗
那么我们就有了一个思路
对于一个范围,我们可以处理这个范围的左范围之后处理右范围,而每个范围都是一直进入左范围,到最后不就到了叶节点,处理完叶节点之后会退回上层处理右边的叶节点,再退回去处理他们的父结点,而这刚好就是后序遍历
所以我们可以写出下面的递归代码,只要当前范围不是叶节点,我们就继续进去处理左范围和右范围,一直到l==r的情况,这种情况也就是说我们只需要判断是1还是0输出即可,然后退回去处理右节点。在这之后,程序会退回到父结点,然后继续判断这个范围是F、B还是I
#include<iostream>
#include<cmath>
using namespace std;
int n;
char t[1050];
void FBI(int l,int r) {
if(l<r) {
FBI(l, (l+r)/2);
FBI((l+r)/2+1,r);
}
bool zero = true;
bool one = true;
for(int i=l;i<=r;i++) {
if(t[i]=='1') zero = false;
else if(t[i]=='0') one = false;
}
if(!zero&&!one) {
printf("F");
}
else if(one&&!zero) {
printf("I");
}
else if(zero&&!one) {
printf("B");
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=pow(2,n);i++) {
cin>>t[i];
}
FBI(1, pow(2,n));
return 0;
}