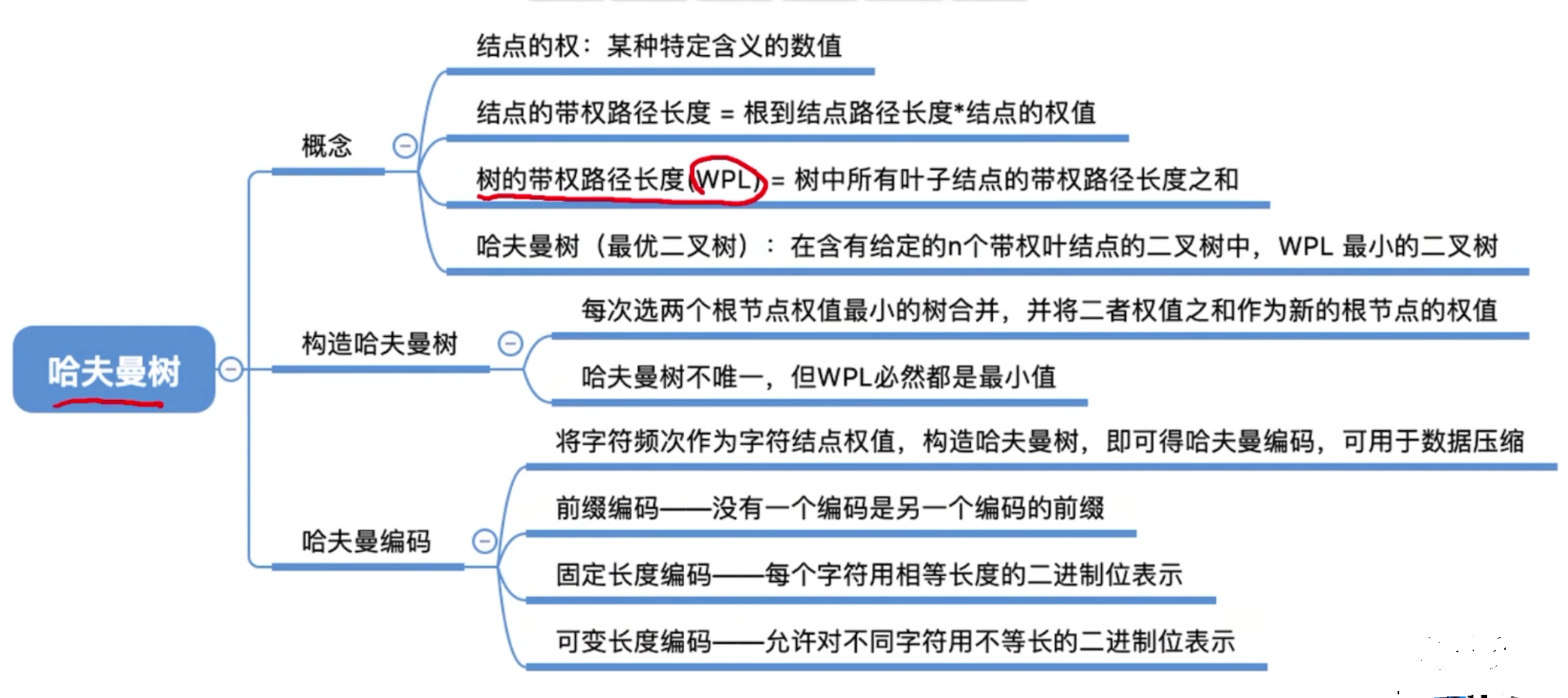
带权路径长度
- 结点的权:有某种现实含义的数值 (如:表示结点的重要性等)
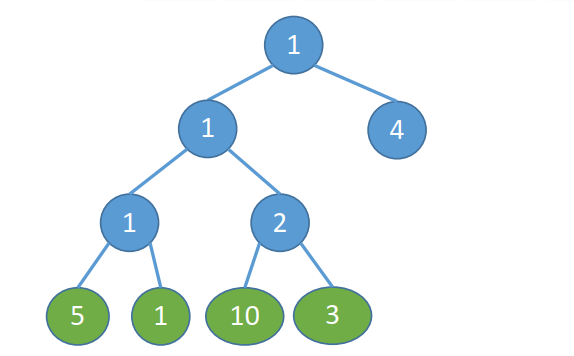
- 结点的带权路径长度:从树的根到该节点的路径长度 (经过的边数) 与该结点上权值的乘积
- 树的带权路径长度:树中所有叶节点的带权路径长度之和 (WPL,Weighted Path Length)
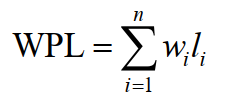
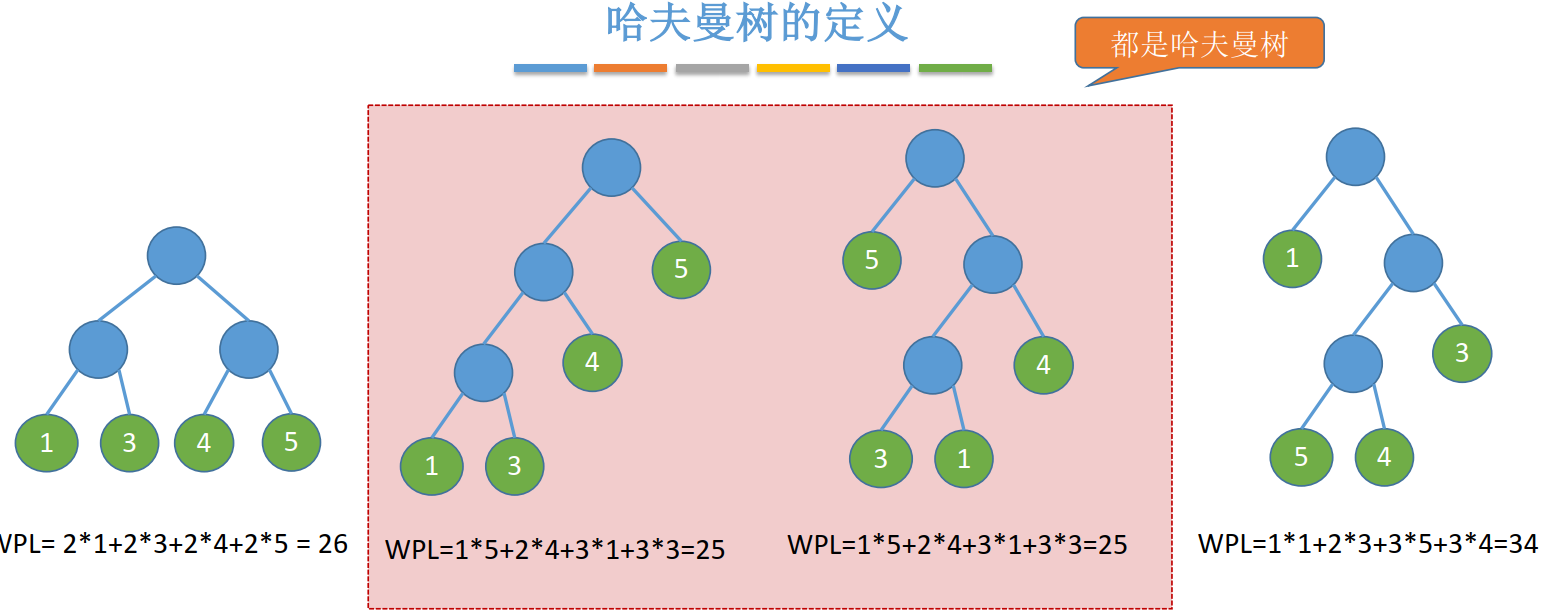
哈夫曼树的定义
在含有 n 个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树
哈夫曼树的构造
给定 n 个权值分别为 w 1 w_1 w1?, w 2 w_2 w2?,…, w n w_n wn?的结点,构造哈夫曼树的算法描述如下:
- 将这 n 个结点分别作为 n 棵仅含有一个结点的二叉树,构成森林 F。
- 构造一个新节点,从 F 中选取两颗根节点权值最小的树作为新根结点的左、右子树,并且将新节点的权值置为左、右子树上的根节点的权值之和。
- 从 F 中删除刚才选出的两颗树,同时将新得到的树加入 F 中。
- 重复步骤 2 和 3,直至 F 中只剩下一颗树为止。
大白话说明
题目

步骤
- 首先将给出的序列排序
- 原数列:19,21,2,3,6,7,10,32
- 排序后:2,3,6,7,10,19,21,32
- 选出两个==最小==的树
- 这里是 2,3
- 将选出的两个数从数列中去除并且将两个数的和放入数列中
- 5,6,7,10,19,21,32
- 重复第一步,直到数列为空。
视频链接如下:
https://www.bilibili.com/video/BV1wX4y1M7TG?spm_id_from=…search-card.all.click
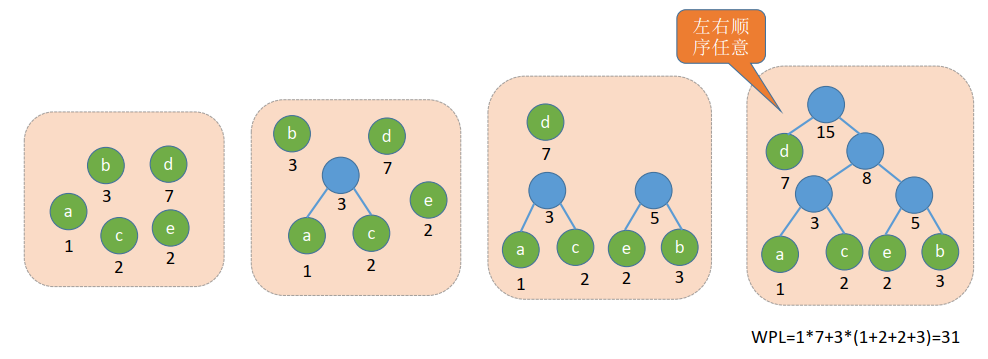
构造步骤如下图:
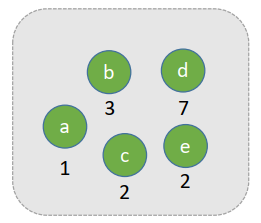

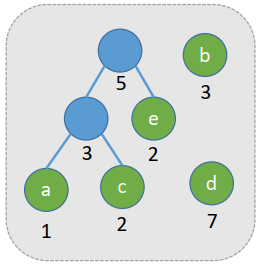

此时树的带权平均路径是最小的,且为: W P L m i n = 1 ? 7 + 2 ? 3 + 3 ? 2 + 4 ? 1 + 4 ? 2 = 31 WPL_{min}=1*7+2*3+3*2+4*1+4*2=31 WPLmin?=1?7+2?3+3?2+4?1+4?2=31
注意
- 每个初始结点最终都称为叶节点,且权值越小的结点到根节点的路径长度越大
- 哈夫曼树的结点总数为 2 n ? 1 2n-1 2n?1
- 哈夫曼树中不存在度为 1 的结点
- 哈夫曼树并不唯一,但 WPL 必然相同且为最优。
哈夫曼编码
电报——点、划两个信号 (二进制 0/1)
固定长度编码——每个字符用相同长度的二进制位表示
ASCII 编码
A —— 0100 0001
B —— 0100 0010
C —— 0100 0011
D —— 0100 0100
每个字符用长度为 2 的二进制表示 (减少长度,提高空间的利用率)
A —— 00
B —— 01
C —— 10
D —— 11
假设,100 个题有 80 题选 C,10 题选 A,8 题选 B,2 题选 D
所有答案的二进制长度为:
80
?
2
+
10
?
2
+
8
?
2
+
2
?
2
=
200
80*2+10*2+8*2+2*2=200
80?2+10?2+8?2+2?2=200bit,而这个转换成树结构为:
按照:左为 0,右为 1 的原则
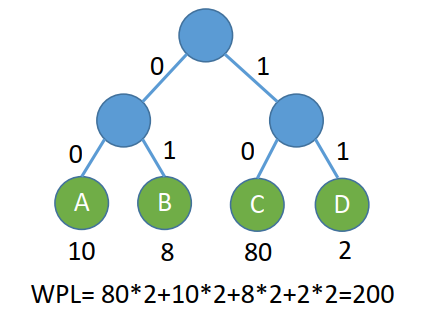
此时 WPL:200,思考是否可以在优化?使用哈夫曼树进行排列,如下图
- C–0(树的路径)
- A–10
- B–111
- D—110
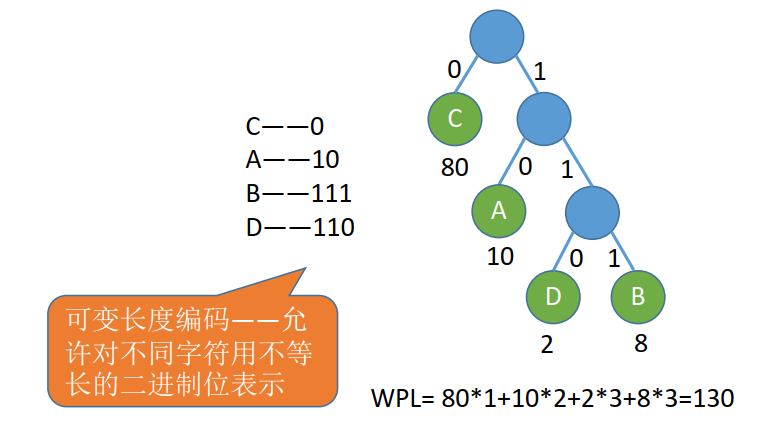
为什么使用叶子节点存储选项
首先,假设使用非叶子节点存储数据,结构如下图:
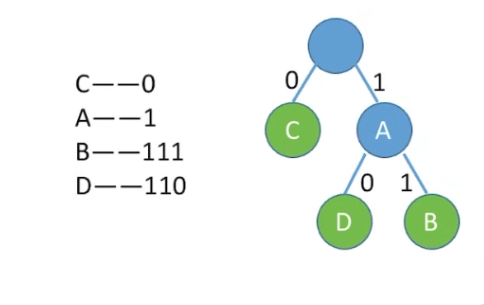
假如传输的数据是:CAAABD,转换成编码就是:0111111110,而此时连续的 111111 就是给解码方带来困惑,会有多种解读意思。
- 可变长度编码:允许对不同字符用不等长的二进制位表示。
- 若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。
- 前缀解码无歧义,非前缀解码有歧义
- 有哈夫曼树得到的哈夫编码——字符集中的每个字符作为一个叶子节点,各个字符出现的频度作为节点的权值,根据之前的介绍 构造哈夫曼树。
- 哈夫曼树编码不唯一
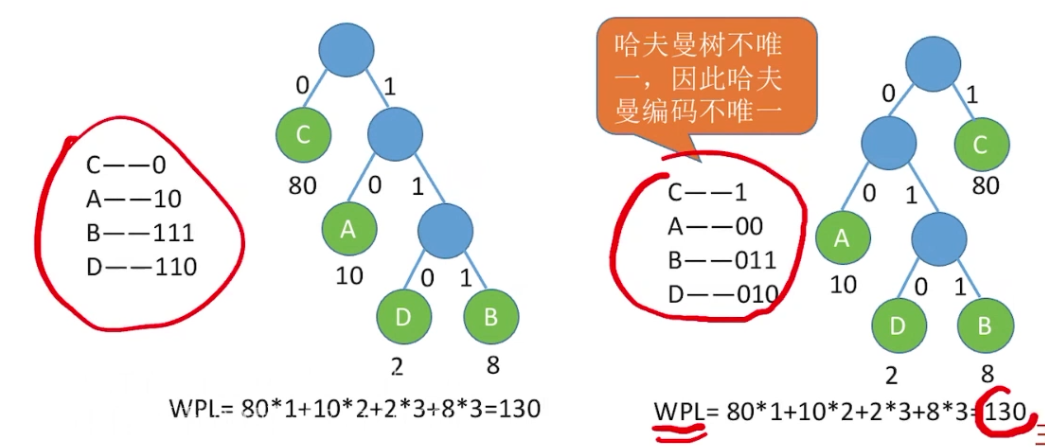
考点
计算英语字母频次

知识回顾与重要考点