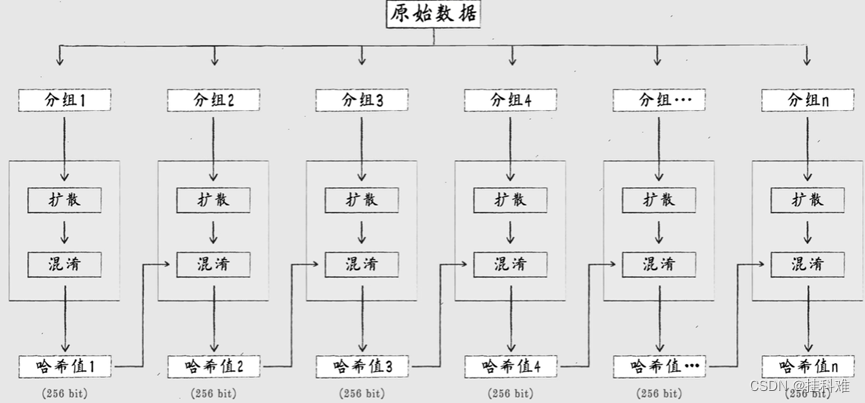
哈希函数
SHA-256的输出有2256中可能性,但输入的信息可以是无限的,所以一定存在两段信息他们的hash值是一样的,MD5已经被攻破了,所以SHA也可以被攻破,但现在还没找到有效的方使。
详解
一段信息可以是任意长,一篇小说,一个数学公式,都算作信息。为了产生同样长度的hash,先对数据进行分组。每组512bit,不够填充。填充会在先补一个bit1,在补bit 0,直到bit长度模512等于448,再补上一个64bit表示信息长度。
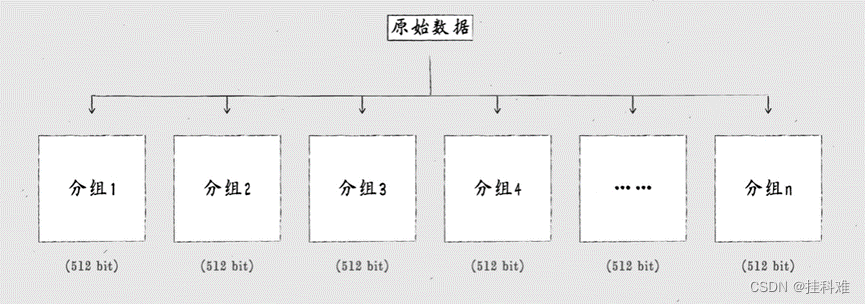
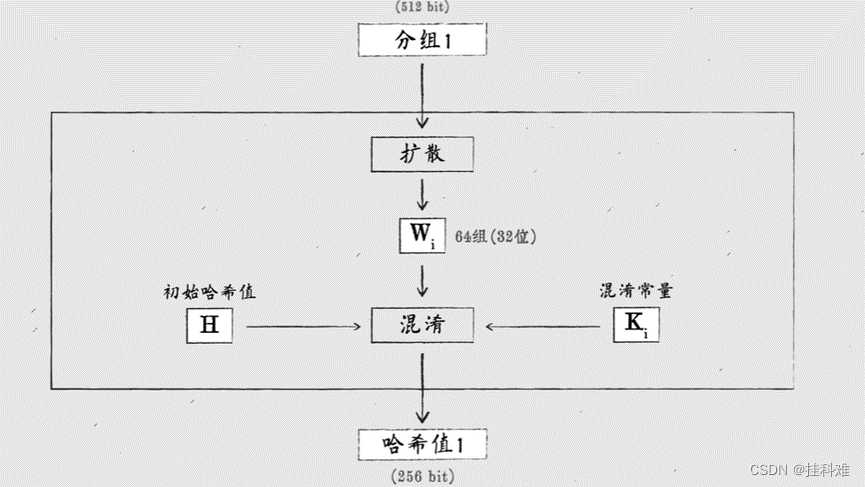
每个分组进行压缩函数处理,也就是扩散和混淆:
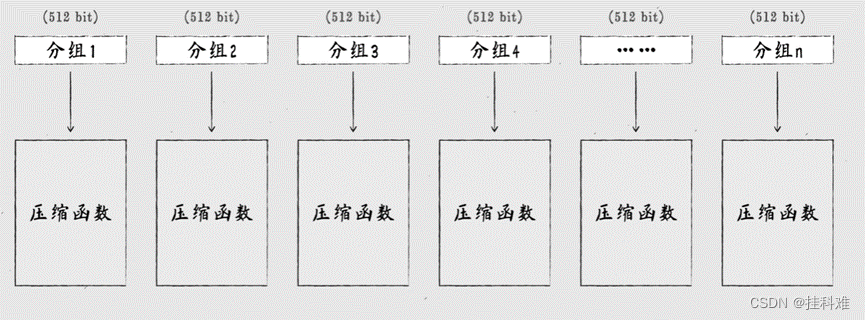
扩散:
每组(512bit)再分成16小组,每小组32bit称为字(word)

将16个字扩散成64个
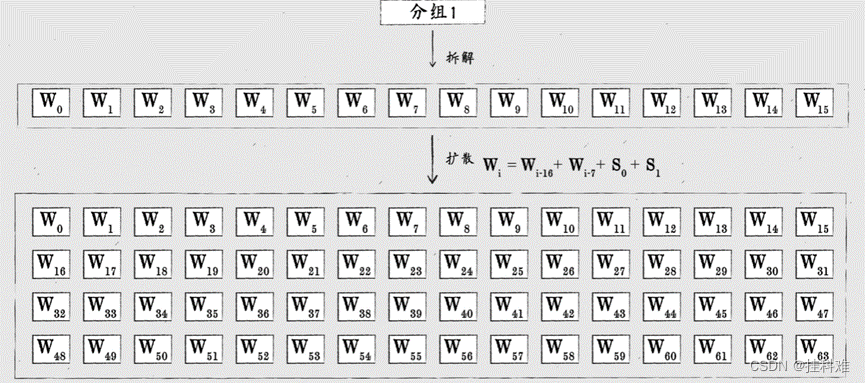
如何扩散?以16为例:
每个数都有前面的四个数运算得到
所有的运算都是在232为模有限域内,即232+1 = 1
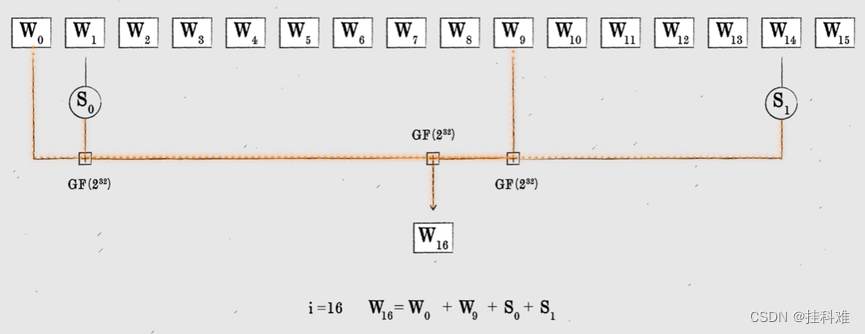
S0,S1函数表示为:

RORT,右移以前面补移除的数
SHR,右移前面补0
最后异或得S0,S1同理得到W_16

W_i被W_(i-16),W_(i-7),W_(i-15), W_(i-2)影响
扩散结束后,得到64个字,每个字均与之前的四个字有关,输入变一点,扩散都会得到不一样的变化
混淆
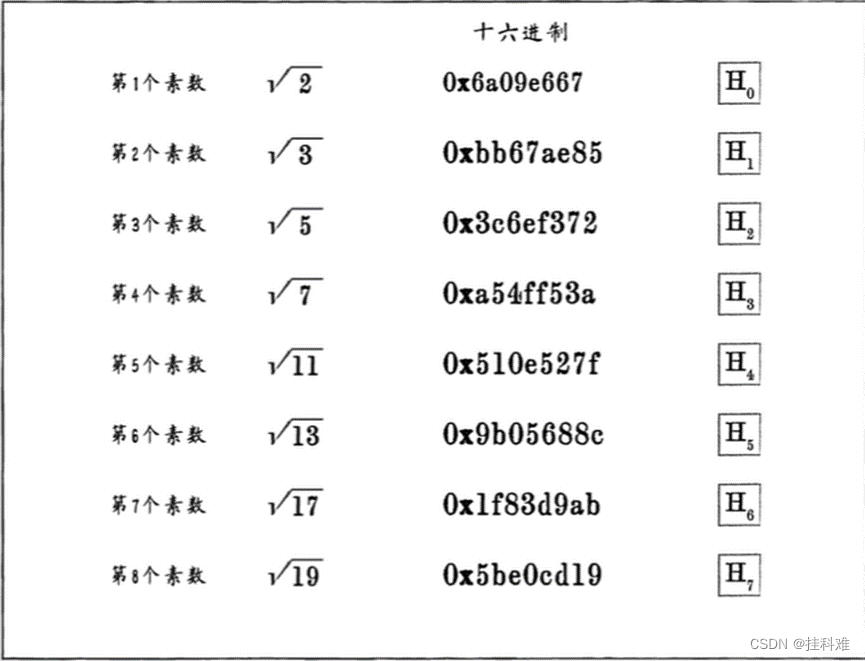
初始哈希值H:最小的8个素数平方根的前32位
混淆常量K:前64个素数立方根的前32位

方便后面讲解,再引入四个函数:两个跨位相加函数

选择函数choose和多数函数majority:

选择函数:公式看着复杂,简单说就是H4为1就取H5的值,H4为0取H6的值

多数函数更好理解,0多取0,1多取1

以第一个字word为例,混淆计算:
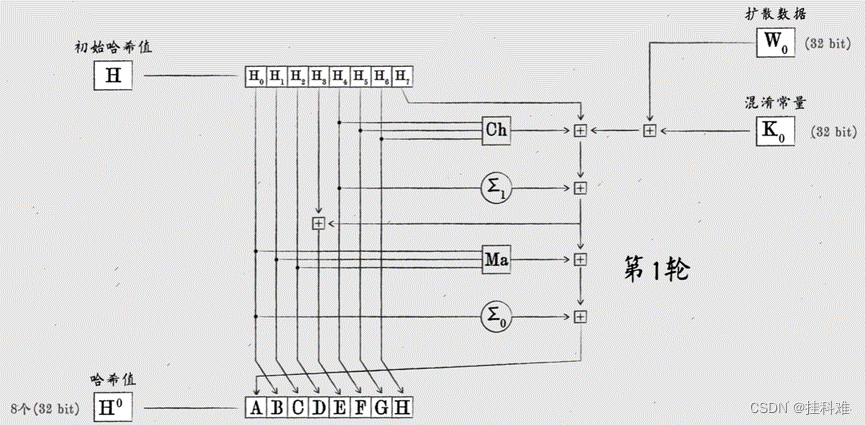
我们有64个扩散后的字,所以这个过程要进行64轮,最后与初始哈希值相加得到这一组(512bit)的hash
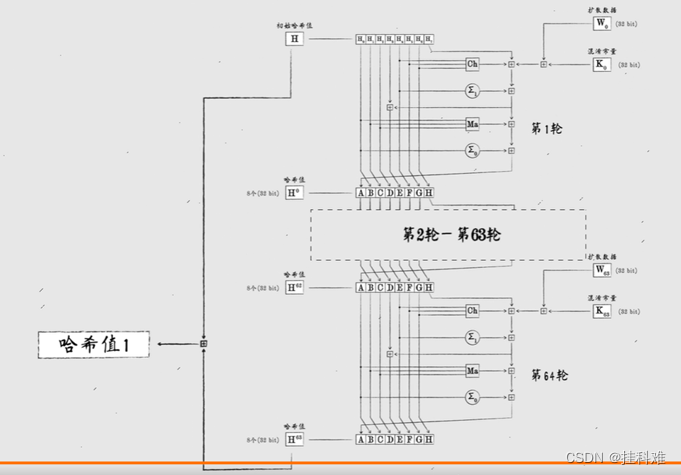
将第一组的hash,哈希值1作为第二组的哈希初始值,,,,循环往复
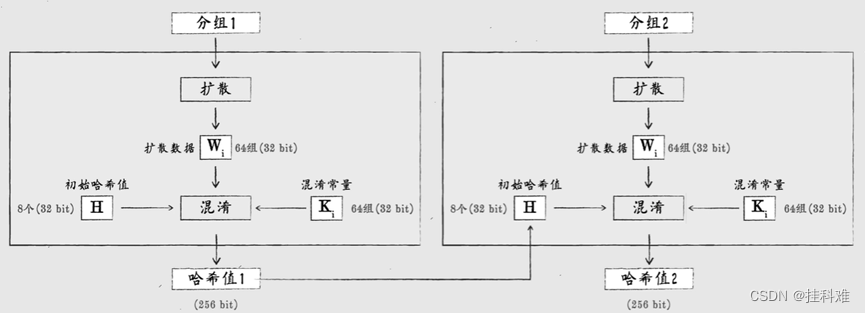
直到最后一组得到的hash才是我们看到的哈希值。