前言：

由于实习面试需要，我需要做个力扣的算法题目，看了力扣上的题解，基本上都是C++,JAVA,Python实现的，虽然可以捡现成的，背下摸摸鱼，但是，为了宣传一波我大CSharp，特意在此用算法实现该题目，为了便于输出打印数组，特意另外写了打印数组的静态函数方法！
第一次写算法题题解博客，如有谬误，敬请批评指正！

一，算法题目描述

一个音乐会总共有 n 排座位，编号从 0 到 n - 1 ，每一排有 m 个座椅，编号为 0 到 m - 1 。你需要设计一个买票系统，针对以下情况进行座位安排：

同一组的 k 位观众坐在同一排座位，且座位连续。
k 位观众中每一位都有座位坐，但他们不一定坐在一起。

由于观众非常挑剔，所以：

只有当一个组里所有成员座位的排数都小于等于 maxRow ，这个组才能订座位。每一组的 maxRow 可能不同。
如果有多排座位可以选择，优先选择最小的排数。如果同一排中有多个座位可以坐，优先选择号码最小的。

请你实现 BookMyShow 类：

BookMyShow(int n, int m) ，初始化对象，n 是排数，m 是每一排的座位数。
int[] gather(int k, int maxRow) 返回长度为 2 的数组，表示 k 个成员中第一个座位的排数和座位编号，这 k 位成员必须坐在同一排座位，且座位连续。换言之，返回最小可能的 r 和 c 满足第 r 排中 [c, c + k - 1] 的座位都是空的，且 r <= maxRow 。如果无法安排座位，返回 [] 。
boolean scatter(int k, int maxRow) 如果组里所有 k 个成员不一定要坐在一起的前提下，都能在第 0 排到第 maxRow 排之间找到座位，那么请返回 true 。这种情况下，每个成员都优先找排数最小，然后是座位编号最小的座位。如果不能安排所有 k 个成员的座位，请返回 false 。

二，基本概念理解：

线段树：

是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。
未优化的空间复杂度为2N，
实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

递归：

程序调用自身的编程技巧称为递归（ recursion）。
一般来说，递归需要有边界条件、递归前进段和递归返回段。
当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

满二叉树：

如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树！
节点：包含一个数据元素及若干指向子树分支的信息
节点的度：一个节点拥有子树的数目称为节点的度
叶子节点：也称为终端节点，没有子树的节点或者度为零的节点

三，例子引入分析

假设我们现在有一个整数段1-10，划为区间为[1,10]（闭区间），实际情况对应的我们有从索引值从1到10的一个数组，比如我们需要查询某个区间的最小值或者修改某段区间的值，那么如何动态高效地去实现这些要求，最好的方法就是使用线段树去维护并实现它们。
我们将1-10区间划分为若干个区间，如下图所示：
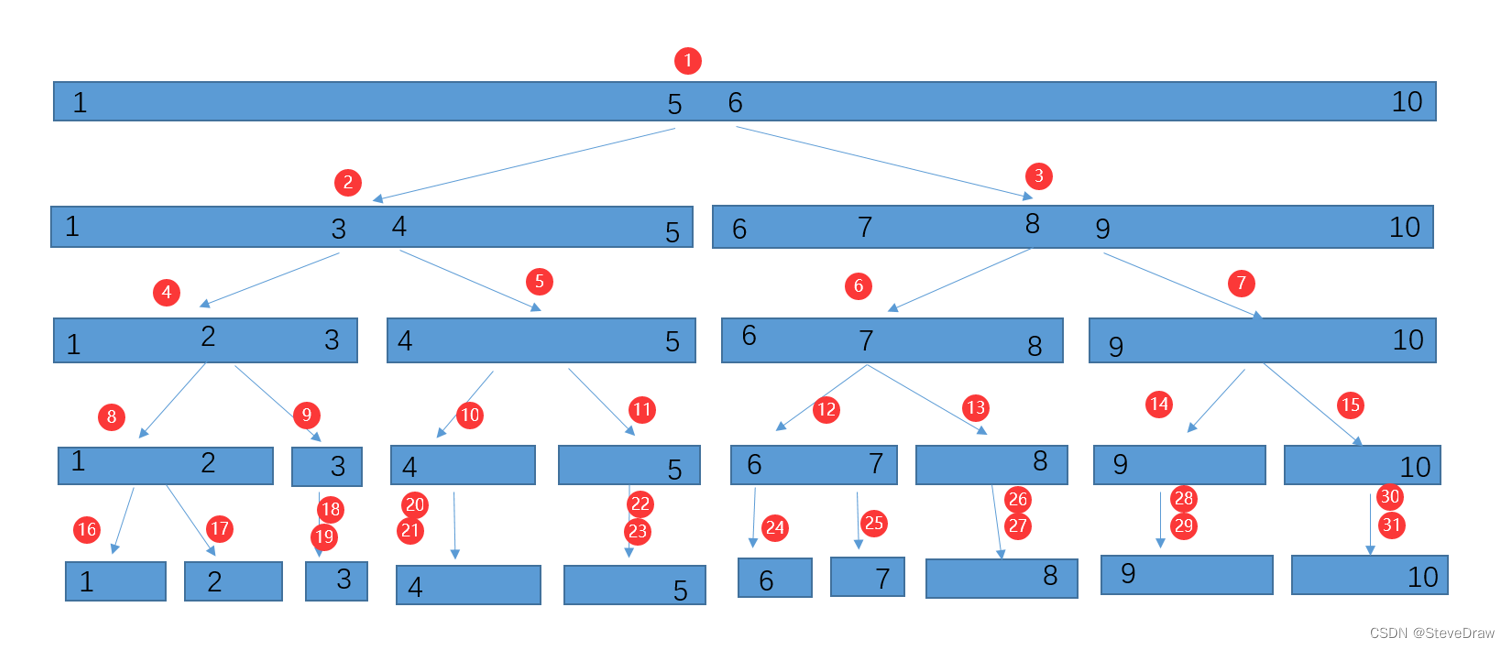
在这里插入图片描述
我们可以使用二分法不断自顶向下划分区间，另外，为了达到满二叉树的要求，我们在倒数第二层进行划分时，由于一些区间已经提前到达叶子，我们还是把这个（单个整数）区间继续二分，已填满二叉树和标号要求！
另外我们需要维护其中的某一段区间（线段树），所以还将某一段区间进行标号，以便在数组中更好的查找和定位，命名规则如下（红色标号即为线段树标号，即下标名）：

一个节点的左子节点名称为，该节点数乘以2；
一个节点的右子节点名称为，该节点数乘以2+1,；
将每层的区间数进行累加，发现总和为：1+2+4+8+16（当做填满的）=31<10x4，而数组长度为10,但需要维护1到n个的整数区间时，我们则需要3n+x个元素的数组，为了方便，我们则需建立4n个数的数组，来做线段树的维护。

四，代码解释

（1）安排座位函数

函数作用：可指定位置开始添加安排座位，并统计安排座位的人数！
函数参数构造：

subs：当前节点的下标（标号）
lp：当前节点（区间）的左端点
rp：当前节点的右端点
idx：安排座位的位置
val：加多少个人（安排多少个座位）

public void Add(int subs, int lp, int rp, int idx, int val)
        {
            if (lp == rp)  //到达叶子，lp=rp=subs
            {
                sum[subs] += val;
                min[subs] += val;
                return;
            }
            var mid = (lp + rp) / 2;
            if (idx <= mid) Add(subs * 2, lp, mid, idx, val);  //递归左子节点
            else Add(subs * 2 + 1, mid + 1, rp, idx, val);     //递归右子节点
            sum[subs] = sum[subs * 2] + sum[subs * 2 + 1];         //维护区间的求和值
            min[subs] = Math.Min(min[subs * 2], min[subs * 2 + 1]);  //取区间内的最小值，利用min函数，Java，c#都有
        }

注意这段代码：sum[subs]=sum[subs2]+sum[subs2+1];，为什么同时累加其左右子节点的值，因为递归不同单元区间所在位置在其左子节点或右子节点的位置，不同单元分布位置则是不同，这也是我们为啥要一直判断是在单元区间的中位值的左边还是右边！

（2）查询函数

函数参数构造：

subs：当前节点的下标（标号）
lp：当前节点（区间）的左端点
rp：当前节点的右端点
LQP：要查询的区间的左端点
RQP：要查询区间的右端点
函数作用：查询指定查询区间内的元素和

分析：我们其实不能直接像之前的判断条件进行递归处理，因为查询区间与线段树的子区间并不刚好重合，有三种关系：

查询区间同时横跨线段树的区间的中值的左边和右边
查询区间位于线段树的某区间的中值的左边
查询区间位于线段树的某区间中值的右边

那么不能像之前安排座位的函数一样的条件进行对应的递归，我们需要重新建立新的布尔判断并进行递归！我们将横跨的左边部分当成（左子）查询区间位于线段树的某区间的中值的左边，将横跨的右边部分当成（右子）查询区间位于线段树的某区间的中值的右边，这样我们就能归化成两种情况：左边和右边！这样他们无论在左边还是右边，都会完全含于对应线段树的子区间内，当满足条件时即可返回对应元素和！
只需将左子查询区间和右子查询区间（包含的线段树的子区间元素值）累加加在一起！即可查询到对应区间的元素和！

我们可以将查询区间与线段树的子区间的三种关系划为两种关系：

完整含于线段树某区间的左边
完整含于线段树某区间的右边

public long QuerySum(int subs, int lp, int rp, int LQP, int RQP)
        {

            if (LQP <= lp && rp <= RQP) return sum[subs];    // 如何查询的区间含于线段树的子区间内，则返回其值      
            long ans = 0;            //返回对应左遍历或右遍历或左右都有的遍历得到的累加数
            var mid = (lp + rp) / 2;
            if (LQP <= mid) ans += QuerySum(subs * 2, lp, mid, LQP, RQP);
            if (RQP > mid) ans += QuerySum(subs * 2 + 1, mid + 1, rp, LQP, RQP);
            return ans;
        }

（2）求出1到RPS内的最小下标

函数参数构造：

subs：当前节点的下标（标号）
lp：当前节点（区间）的左端点
rp：当前节点的右端点
RPS：可支持的maxrow+1的值
val:一排中的空位
函数作用：返回[1,maxRow+1]的最小下标

public int Indexs(int subs, int lp, int rp, int RPS, int val)
        {
            if (min[subs] > val) return 0;          //无法安排现有的空位，则返回0
            if (lp == rp) return lp;                 //达到叶子即可返回下标，lp=rp=subs,
            var mid = (lp + rp) / 2;
            if (min[subs * 2] <= val) return Indexs(subs * 2, lp, mid, RPS, val);
            if (mid < RPS) return Indexs(subs * 2 + 1, mid + 1, rp, RPS, val);
            return 0;
        }

分析：
我们需要检索出1到maxRow+1内的最小下标，那么使用的是最小值线段树，对该线段树进行处理维护即可，那么我们需要获取可以连续坐k个人的最小行数（1到maxrow内），换句话来说：我们这行可以至少安排k个人，或空位少于m-k的值，那么如果满足这些条件，即可返回对应的下标，另外左右递归时条件注意下！
我们是从前往后找出最小下标，所以首先递归左子区间（所以布尔条件为左子区间的最小值是否能达到要求）；
其次，我们的左子区间都不满足时，但mid小于maxRow时就需要对其右递归！

（3）gather函数

函数参数构造：

k:需要连续安排的小组人数
maxRow：小组要求的排位最大值
函数作用：返回长度为 2 的数组，表示 k 个成员中第一个座位的排数和座位编号

       public int[] Gather(int k, int MaxRow)
        {
            int i = Indexs(1, 1, n, MaxRow + 1, m - k);  //返回1到，maxrow+1间的最小下标
            if (i == 0) return new int[] { };            // 若无返回空数组
            var seats = (int)QuerySum(1, 1, n, i, i);        //查询最小下标元素个数
            Add(1, 1, n, i, k);                     //安排座位
            return new int[] { i - 1, seats };      //返回要求的数组元素
        }

分析：
通过查找出最小下标，将其传入到查询函数和安排座位函数进而完成题目要求！
注意：最小下标是从1开始的，而返回数组是从0开始的，所以我们需要i-1

（4）scatter函数

函数参数构造：

k:需要连续安排的小组人数
maxRow：小组要求的排位最大值
函数作用：如果组里所有 k 个成员不一定要坐在一起的前提下，都能在第 0 排到第 maxRow 排之间找到座位，那么请返回 true。否则，返回false！

public bool Scatter(int k, int MaxRow)
        {
            var seat = (long)(MaxRow + 1) * m - QuerySum(1, 1, n, 1, MaxRow + 1);         //得到总的剩余空位
            if (seat < k) return false;
            var i = Indexs(1, 1, n, MaxRow + 1, m - 1);         //返回至少能做1个人以上的最小下标
            while (true)
            {
                int seats = m - (int)QuerySum(1, 1, n, i, i);  //得到一列中剩余的空位
                if (k < seats)
                {
                    Add(1, 1, n, i, k);
                    return true;
                }
                k -= seats;
                Add(1, 1, n, i, seats);
                i += 1;

            }
        }

分析：
如果一列中可以刚好可以安排一个小组，就直接返回true，否则，先安排可以做到空位，然后安排座位数就减去已安排的数目，以此反复，最终使得满足条件返回True，跳出循环！

（5）复杂度简要分析

时间复杂度：
- 初始化为 O(n)。初始化线段树需要O(n)。
- gather 为 O(logn)。
- Scatter 可以从整体上来分析：我们要么在填充空排，要么在填充受之前操作影响的未填满的排，所以所有 scatter 操作的复杂度之和为 O((n+q)logn)，这里 Gather 和 Scatter 的调用次数之和。注意上述题解中的「从第一个未坐满的排开始占座」保证了总体复杂度不会退化至 O(nq)。
空间复杂度：O(n)。线段树需要 O(n) 的空间。

五，总体代码

算法的相关函数部分我将它们封装成BookMyShow类的方法，并在主程序添加处理打印对应类型的数组，并调用相关方法以达到处理目的！刚开始的话我将sum这个线段树和查询返回是int结果误差挺大的，后来改成long，后来提交给力扣也100通过！
可以看我的博文：数组对应方法

（1）BookMyShow.cs

using System;

namespace MusicSelectV1._0
{
    class BookMyShow
    {
        private int n;      //剧院n排座位
        private int m;         //剧院m列座位
        public long[] sum;   //用于求和的线段树
        public int[] min;  //用于求最小值的线段树
        public BookMyShow(int n, int m)
        {
            this.n = n;
            this.m = m;
            sum = new long[n * 4];//由于线段树需要维护子区间的个数需在一定范围，为了不超过维护边界而定的数目
            min = new int[n * 4];
        }
        public void Add(int subs, int lp, int rp, int idx, int val)
        {
            if (lp == rp)  //到达叶子，lp=rp=subs
            {
                sum[subs] += val;
                min[subs] += val;
                return;
            }
            var mid = (lp + rp) / 2;
            if (idx <= mid) Add(subs * 2, lp, mid, idx, val);  //递归左子节点
            else Add(subs * 2 + 1, mid + 1, rp, idx, val);     //递归右子节点
            sum[subs] = sum[subs * 2] + sum[subs * 2 + 1];         //维护区间的求和值
            min[subs] = Math.Min(min[subs * 2], min[subs * 2 + 1]);  //取区间内的最小值，利用min函数，Java，c#都有
        }
        public long QuerySum(int subs, int lp, int rp, int LQP, int RQP)
        {

            if (LQP <= lp && rp <= RQP) return sum[subs];    // 如何查询的区间含于线段树的子区间内，则返回其值      
            long ans = 0;            //返回对应左遍历或右遍历或左右都有的遍历得到的累加数
            var mid = (lp + rp) / 2;
            if (LQP <= mid) ans += QuerySum(subs * 2, lp, mid, LQP, RQP);
            if (RQP > mid) ans += QuerySum(subs * 2 + 1, mid + 1, rp, LQP, RQP);
            return ans;
        }
        public int Indexs(int subs, int lp, int rp, int RPS, int val)
        {
            if (min[subs] > val) return 0;          //无法安排现有的空位，则返回0
            if (lp == rp) return lp;                 //达到叶子即可返回下标，lp=rp=subs,
            var mid = (lp + rp) / 2;
            if (min[subs * 2] <= val) return Indexs(subs * 2, lp, mid, RPS, val);
            if (mid < RPS) return Indexs(subs * 2 + 1, mid + 1, rp, RPS, val);
            return 0;
        }
        public int[] Gather(int k, int MaxRow)
        {
            int i = Indexs(1, 1, n, MaxRow + 1, m - k);  //返回1到，maxrow+1间的最小下标
            if (i == 0) return new int[] { };            // 若无返回空数组
            var seats = (int)QuerySum(1, 1, n, i, i);        //查询最小下标元素个数
            Add(1, 1, n, i, k);                     //安排座位
            return new int[] { i - 1, seats };      //返回要求的数组元素
        }
        public bool Scatter(int k, int MaxRow)
        {
            var seat = (long)(MaxRow + 1) * m - QuerySum(1, 1, n, 1, MaxRow + 1);         //得到总的剩余空位
            if (seat < k) return false;
            var i = Indexs(1, 1, n, MaxRow + 1, m - 1);         //返回至少能做1个人以上的最小下标
            while (true)
            {
                int seats = m - (int)QuerySum(1, 1, n, i, i);  //得到一列中剩余的空位
                if (k < seats)
                {
                    Add(1, 1, n, i, k);
                    return true;
                }
                k -= seats;
                Add(1, 1, n, i, seats);
                i += 1;

            }
        }
    }
}

（2）入口点主函数

using static System.Console;

namespace MusicSelectV1._0
{
    class Program
    {
        static void PrintArray(int[]b)
        {
            if (b.Length != 0)
            {
                string str = "";
                foreach (var i in b)
                {
                    str = str + i + ",";
                }

                WriteLine("[" + str.Substring(0, str.Length - 1) + "]");
            }
            if (b.Length == 0) WriteLine("[]");
        }
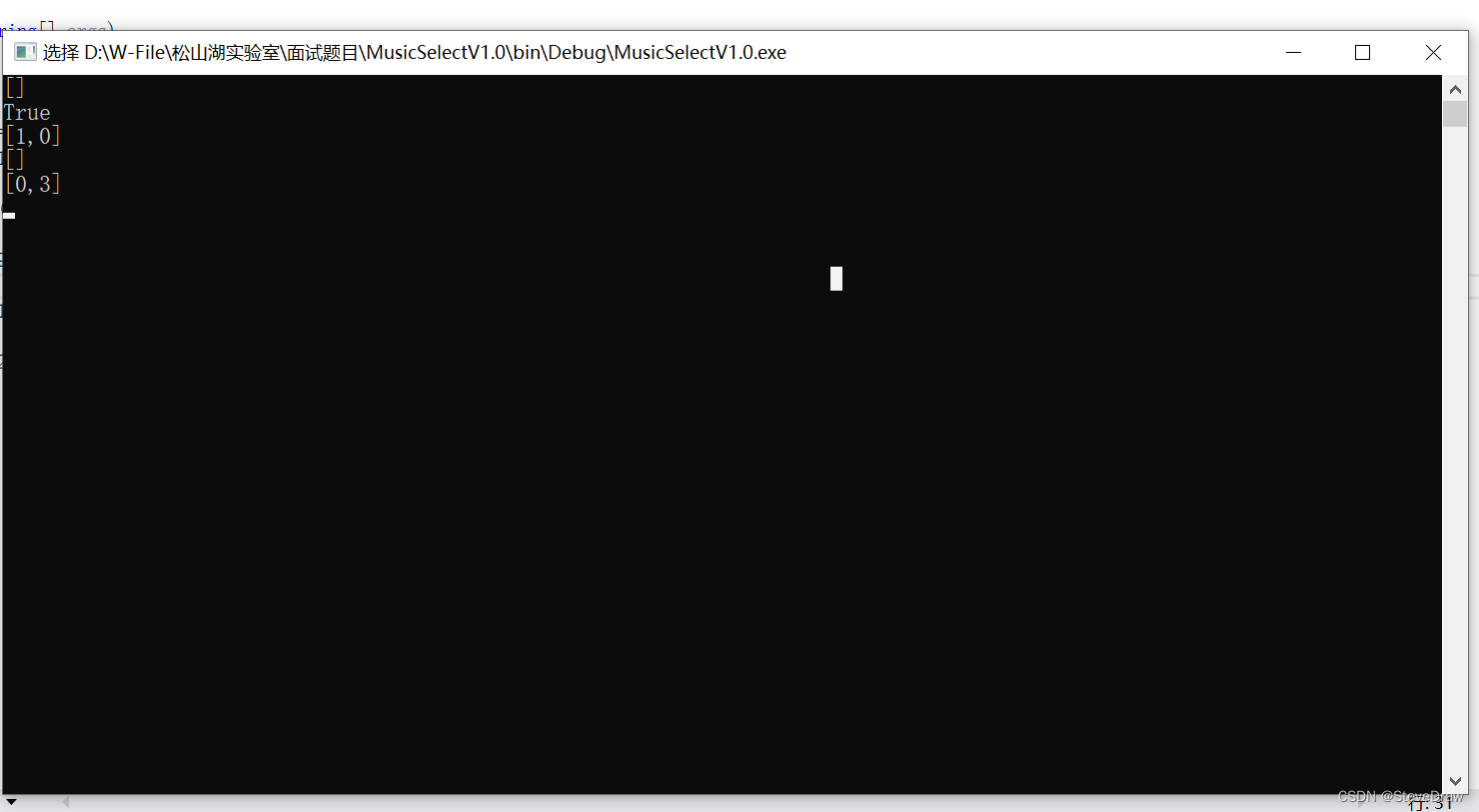
        static void Main(string[] args)
        {
            int[] a;
            bool b;
            BookMyShow bms = new BookMyShow(5, 9);
            a = bms.Gather(10, 1);
            PrintArray(a);
            b = bms.Scatter(3, 3);
            WriteLine(b);
            a = bms.Gather(9, 1);
            PrintArray(a);
            a = bms.Gather(10, 2);
            PrintArray(a);
            a = bms.Gather(2, 0);
            PrintArray(a);
            ReadKey();
        }
    }
}