了解回溯法
回溯法,又叫试探法,是一种寻找最优解的暴力搜寻法。但是,由于暴力,回溯法的时间复杂度较高,因此在比较一些数字较大的问题时,比如上次我们提到的最短路径问题等,运行时间一般比较长。在回溯法中,深度优先搜索是一种很重要的工具。
我们知道,回溯法基本思想是:
(1)针对具体问题,定义问题的解空间;
(2)确定易于搜索的解空间结构(数据结构的选择)。
(3)一般以DFS的方式搜索解空间。
(4)在搜索过程中,可以使用剪枝函数等来优化算法。(剪枝函数:用约束函数和限界函数剪去得不到最优解的子树,统称为剪枝函数。)
DFS的基本思想是:
(1)某一种可能情况向前探索,并生成一个子节点。
(2)过程中,一旦发现原来的选择不符合要求,就回溯至父亲结点,然后重新选择另一方向,再次生成子结点,继续向前探索。
(3)如此反复进行,直至求得最优解。
TSP问题描述

TSP 的递归回溯算法

TSP 的迭代回溯算法

TSP 的时间复杂度分析

代码
#include<iostream>
using namespace std;
/*回溯法求解TSP问题,采用排列树、深度优选搜索的方法
由于课本中没有给出算法,故在此给出算法设计
变量:
1.城市个数n
2.城市之间的距离value[][]
3.城市走过的路程cl
4.最短路径bestx[]
5.城市编号数组x[]
步骤:
*/
#define MAXLENGTH 10
//城市个数
int n;
//城市之间的距离
int value[MAXLENGTH][MAXLENGTH];
//城市编号
int citys[MAXLENGTH];
//最优路径
int bestx[MAXLENGTH];
int maybex[MAXLENGTH];
//经过的路径
int cl = 0;
//最优路径长度
int bestl = 999;
int maybel = 999;
//修正函数原型声明
void Modify();
//Tsp函数原型声明
void Tsp(int n);
int main(){
//计数使用
int i, j;
printf("请输入城市个数:");
scanf("%d", &n);
printf("请输入城市代价矩阵:\n");
for ( i = 1; i <= n; i++)
{
for ( j = 1; j <= n; j++)
{
scanf("%d", &value[i][j]);
}
}
Modify();
//初始化城市编号,最优路径矩阵
for ( i = 1; i <= n; i++)
{
citys[i] = i;
bestx[i] = 0;
}
Tsp(2);
//进行结果输出
printf("最优路线为:\n");
for ( i = 1; i <= n; i++)
{
printf("%4d", bestx[i]);
}
printf("%4d\n", bestx[1]);
printf("最短长度为:%d\n", bestl);
getchar();
getchar();
getchar();
return 0;
}
//修正函数,将对角线数据置为0
void Modify(){
for (int i = 1; i <= n; i++)
{
value[i][i] = -1;
}
}
//交换函数
void swap(int &a, int &b){
int temp;
temp = a;
a = b;
b = temp;
}
//定义回溯法求TSP问题
void Tsp(int t){
//用于计数
int j;
//到达叶子节点
if (t>n)
{
if (value[n][1] != -1){
//记录所经过的路径
printf("可能的路径为:");
for ( j = 1; j <= n; j++)
{
maybex[j] = citys[j];
printf("%4d", maybex[j]);
}
printf("长度:%d\n", cl + value[citys[n]][1]);
}
if (value[citys[n]][1] != -1 && (cl + value[citys[n]][1])<bestl){
//记录所经过的路径
for (j = 1; j <= n; j++)
{
bestx[j] = citys[j];
}
bestl = cl + value[citys[n]][1];
}
}
else{//还没有到达叶子节点
//搜索扩展节点的左右分支,即所有与当前城市所在的邻近城市
for ( j = t; j <= n ; j++)
{
//若果第t-1个城市与第t个城市之间有路径且可以得到更短的路线
if (value[citys[t - 1]][citys[j]] != -1 && (cl + value[citys[t - 1]][citys[j]]) < bestl){
//交换位置
swap(citys[t], citys[j]);
//为长度赋值
cl += value[citys[t - 1]][citys[t]];
//进行深度遍历
Tsp(t + 1);
//恢复原状
cl -= value[citys[t - 1]][citys[t]];
swap(citys[t], citys[j]);
}
}
}
}
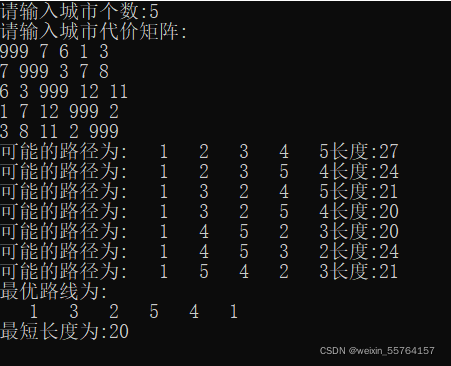
结果