[数据结构与算法]【MATLAB】求解约束条件下的目标函数最值（fmincon用法解析）

一、简介

Matlab 的函数 fmincon 用来求最小约束非线性多变量函数，是一个非线性编程求解器，算出指定的问题的最小值。

注： fmincon 同样可以用来求约束条件下的最大值，主要将目标函数取反（前面加一个负号）即可。

二、fmincon()的基本形式与参数

[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

输入参数：

1. fun 是目标函数，注意需要单引号，或者@，（即写为符号函数）；
2. x0函数fun参数值的初始化；
3. 参数值的线性不等式约束 A, b；（A * x <= b）
4. 参数值的等式线性约束 Aeq, beq; (Aeq * x = beq)
5. 参数值的上界和下界 lb, ub
6. 使用 options 所指定的优化选项执行最小化。使用 optimoptions 可设置这些选项。
7. 非线性约束nonlcon，其参数值一般为约束函数。如果没有非线性不等式或等式约束，请设置 nonlcon = []。

输出参数：

1. X 输出最优参数值
2. Fval 输出 fun 在X参数的值
3. Exitflag 输出fmincon额外条件值

fmincon 求解函数的基本形式：

三、约束条件类型与参数写法

约束条件下的函数极值有是三种情况
（1）线性不等式约束；
（2）线性等式约束；
（3）非线性不等式和等式约束；

1.线性不等式约束（参数写法）

线性不等式约束条件如下：

将不等式化为矩阵形式：

fmincon函数的参数可以确定为：

A = [1,2; 3,4; 5,6]; 
b = [10; 20; 30];

2.线性等式约束（参数写法）

线性等式约束条件如下：

同理转换为矩阵后，可知约束参数为：

Aeq = [1,2,3; 2,4,1]; 
beq = [10; 20];

3.非线性约束（参数写法）

非线性约束条件如下：

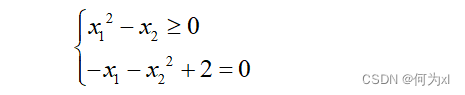
确认为参数时，需要设置为函数形式、。

function [c,ceq]=mycon(x)
c=-x(1)^2+x(2);  %此处不要忘记将不等式改成不等式<=0的标准形式
ceq=-x(1)-x(2)^2+2;

注：函数调用时，nonlcon 参数值为 ‘函数名’

四、例题

（1）线性不等式约束下求最值示例

以上是关于求目标函数

$f=100?（x_2?x_1{）}^2+(1?x_1{)}^2$

在线性约束 $x_1+2x_2\le 1$ 条件下的最小值，结果如下：

目标函数：

function f = fminx(x)
    f = 100 * (x(2) - x(1)).^2 + (1-x(1)).^2;
end

fmincon函数的使用：

[x,fval,exitflag] = fmincon(@(x) fminx(x),[0,0],[1,2],[1])

结果：

x =

    0.3363    0.3319


fval =

    0.4425


exitflag =

     1

注：结果含义为 在$x_1=0.3363,x_2=0.3319时，取最小值：y=0.4425$

（2）线性不等式和等式约束条件下求最值示例

目标函数： $f=100?（x_2?x_1{）}^2+(1?x_1{)}^2$
约束条件：

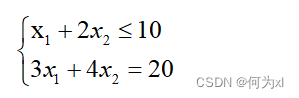
这次使用目标函数为匿名函数的方式，一步到位：

fun=@(x)100*(x(2)-x(1))^2+(1-x(1))^2;
x0=[0,0];
A=[1,2];
b=10;
Aeq=[3,4];
beq=20;
[x,fval,exitflag] = fmincon(fun,x0,A,b,Aeq,beq)

结果为：

x =

    2.8511    2.8617


fval =

    3.4378


exitflag =

     1

（3）非线性约束下求最值示例

上面两题只有目标函数是非线性的，如果其约束条件也是非线性的，我们又该怎么办呢？

示例1：

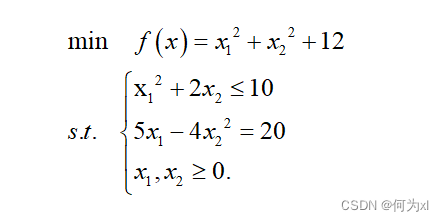
目标函数求值代码：

fun=@(x)x(1)^2+x(2)^2+12;
x0=rand(2,1);
A=[];   
Aeq=[];
b=[];
beq=[];
lb=[0,0];
ub=[];
exitflag=1;
[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,'mycon')

非线性约束条件:

function [c,ceq]=mycon(x)
c=x(1)^2+2*x(2); 
ceq=5*x(1)-4*x(2)^2-20;

结果为：

x =

    1.2471
    0.0000


fval =

   13.5552


exitflag =

    -2

示例2：

目标函数为: $fun=100?(x_2?x_1{)}^2+(1?x_1{)}^2$

约束条件：在以$（1/3，1/3）$为圆心，1/3 为半径,$0\le x_1\le 0.5，0.2\le x_2\le 0.8$ 的边界约束

function f=fun1(x)
f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;
end

function [g,h]=fun2(x)
g=(x(1)-1/3)^2+(x(2)-1/3)^2-1/9;
h=[];
end

[x,y]=fmincon('fun1',[1/3,1/3],[],[],[],[],lb,ub,'fun2')

结果如下:

x =
    0.5000    0.2500
y =
    0.2500

五、总结

非线性规划求最值的fmincon函数其实和线性规划的improg大同小异，关键是对非线性约束条件的把握，即nonlcon，以及option（一般情况下我们不用管，默认值就可以了，有需求具体查阅使用即可）。

参考博客|：

https://blog.csdn.net/qq_52753078/article/details/121244164

https://blog.csdn.net/qq_36932020/article/details/98670486